Class 10 Maths Chapter 14 Statistics (English + Hindi) NCERT Solutions

Class 10 Maths Chapter 14 Statistics (English + Hindi) NCERT Solutions

Table Of Conent

• Ex.14.1
• Ex.14.2
• Ex.14.3
• Ex.14.4
• Ex.14.5
• Statistics Class 10 Extra Questions
• Statistics Class 10 Important Questions
• Statistics Class 10 Notes

Ex 14.1

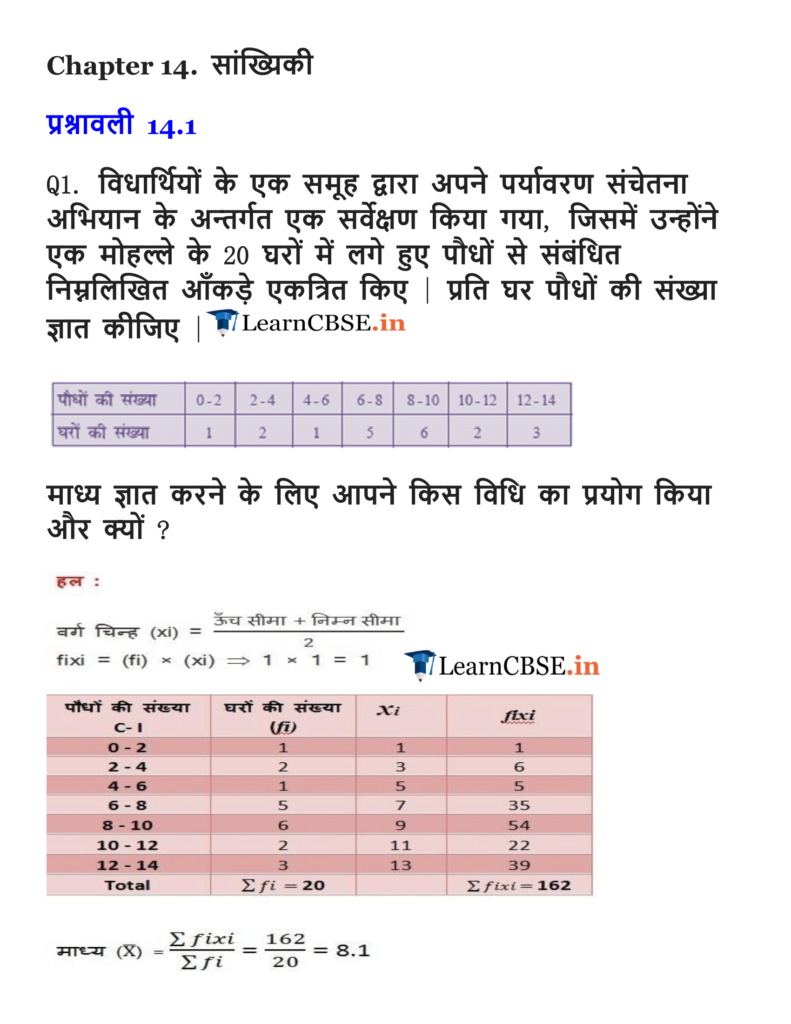
Ex 14.1 Class 10 Maths Question 1.
A survey was conducted by a group of students as a part of their environment awareness programme, in which they collected the following data regarding the number of plants in 20 houses in a locality. Find the mean number of plants per house.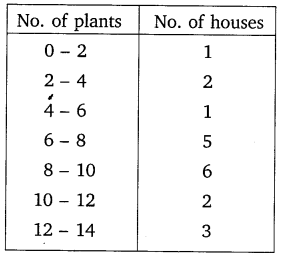

Which method did you use for finding the mean, and why?
Solution: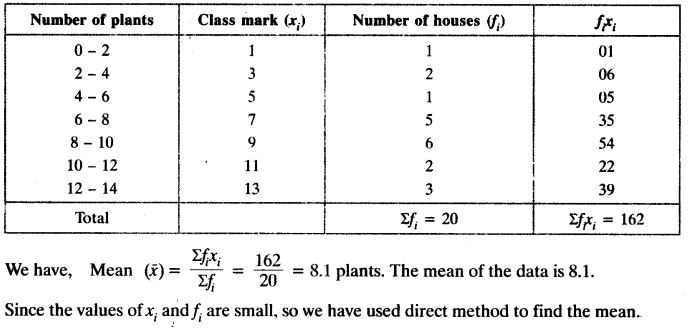

You can also download the free PDF of  Ex 14.1 Class 10 Statistics NCERT Solutions or save the solution images and take the print out to keep it handy for your exam preparation.

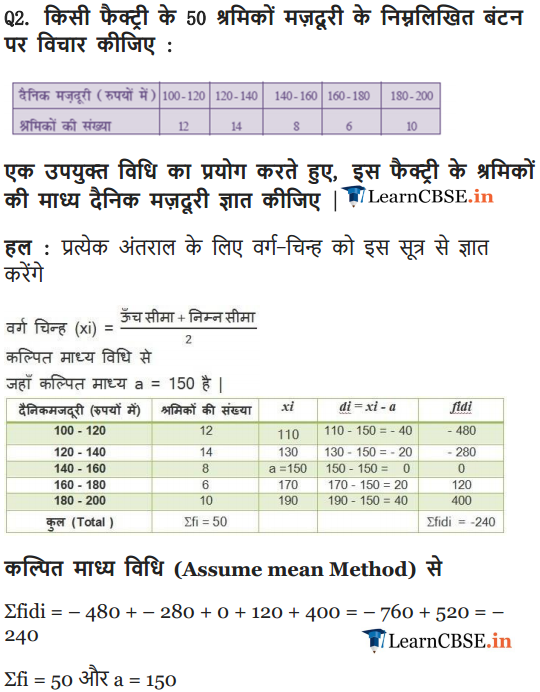
Ex 14.1 Class 10 Maths Question 2.
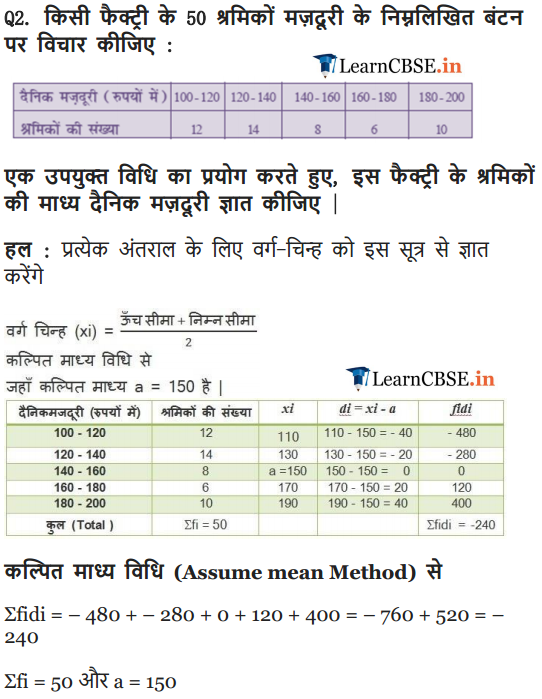
Consider the following distribution of daily wages of 50 workers of a factory.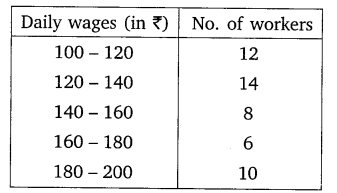

Find the mean daily wages of the workers of the factory by using an appropriate method.
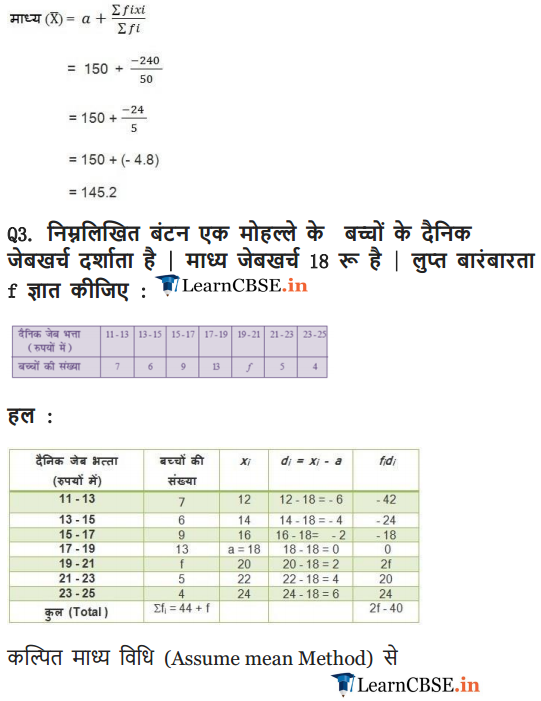
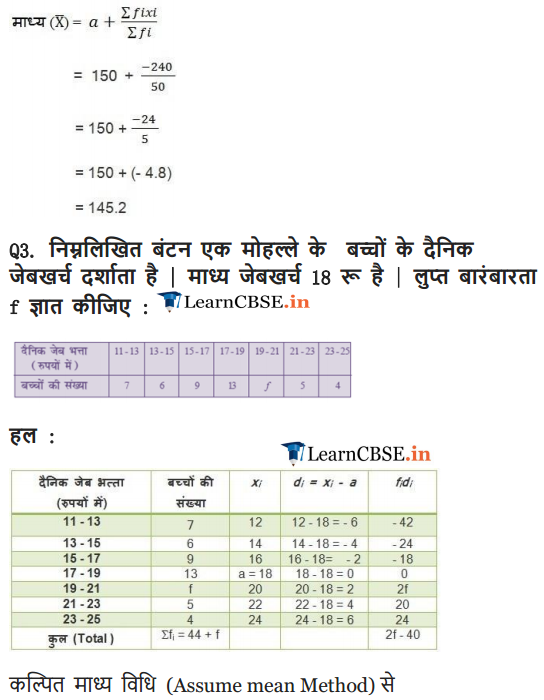
Solution: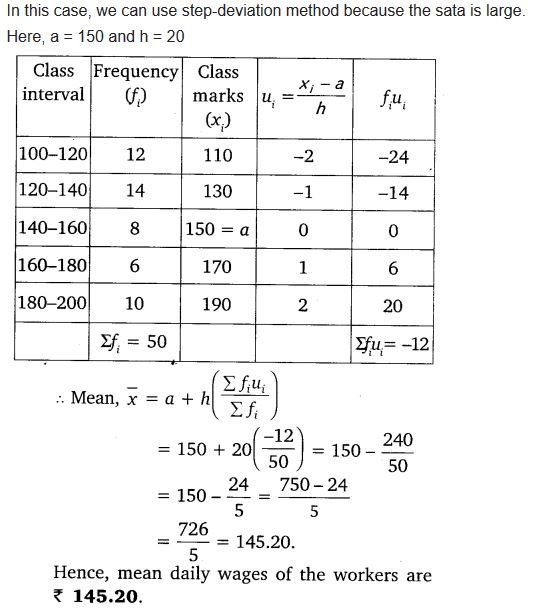

Ex 14.1 Class 10 Maths Question 3.
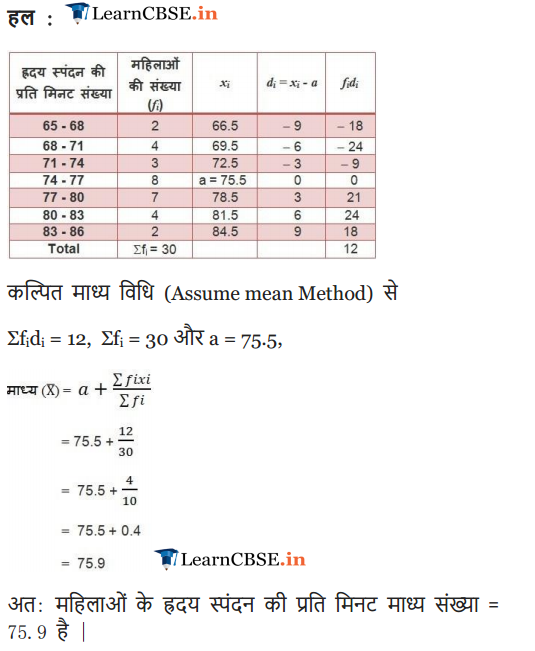
The following distribution shows the daily pocket allowance of children of a locality. The mean pocket allowance is ₹ 18. Find the missing frequency f.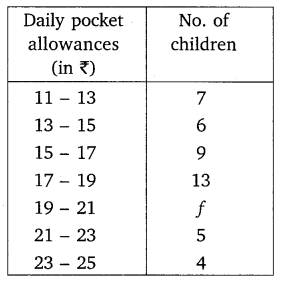

Solution:

Ex 14.1 Class 10 Maths Question 4.
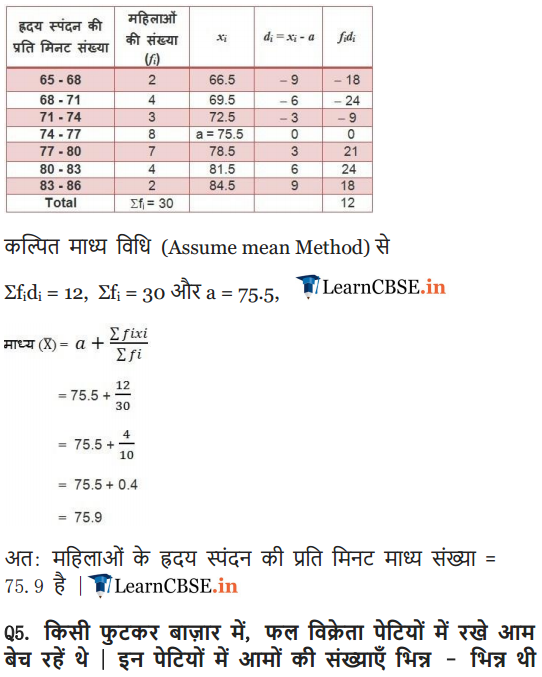
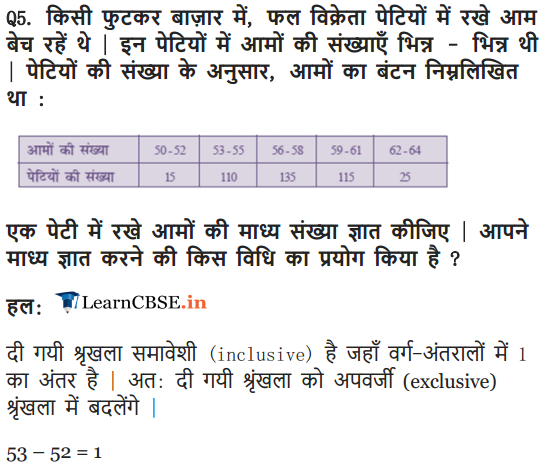
Thirty women were examined in a hospital by a doctor and the number of heart beats per minute were recorded and summarised as follows. Find the mean heart beats per minute for these women, choosing a suitable method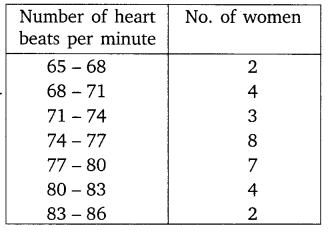

Solution: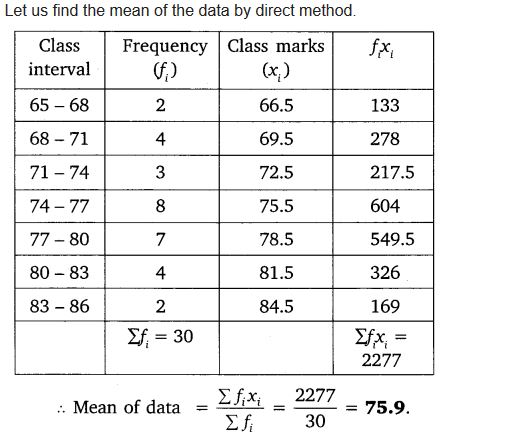

Ex 14.1 Class 10 Maths Question 5.
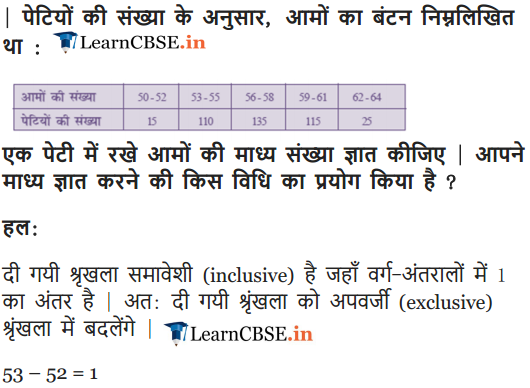
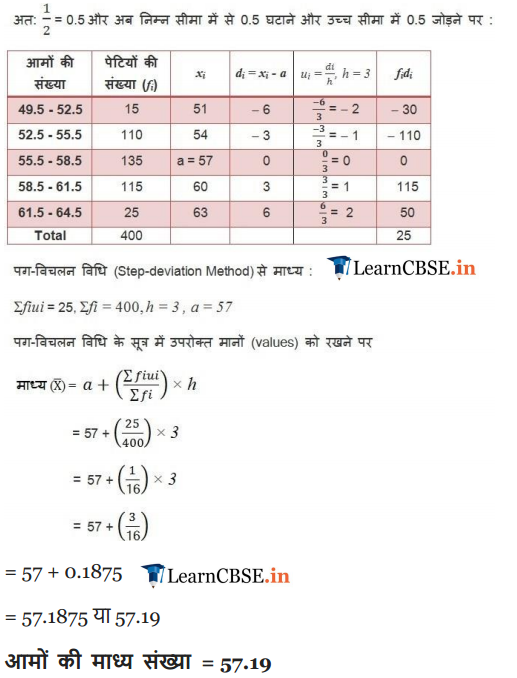
In a retail market, fruit vendors were selling mangoes kept in packing boxes. These boxes contained varying number of mangoes. The following was the distribution of mangoes according to the number of boxes.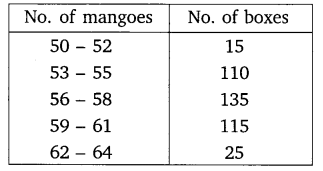

Find the mean number of mangoes kept in a packing box. Which method of finding the mean did you choose?
Solution: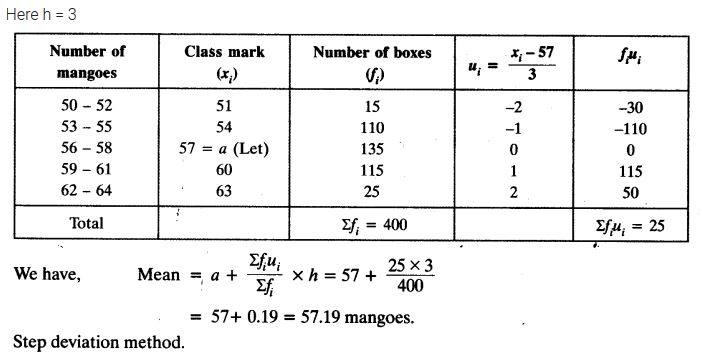

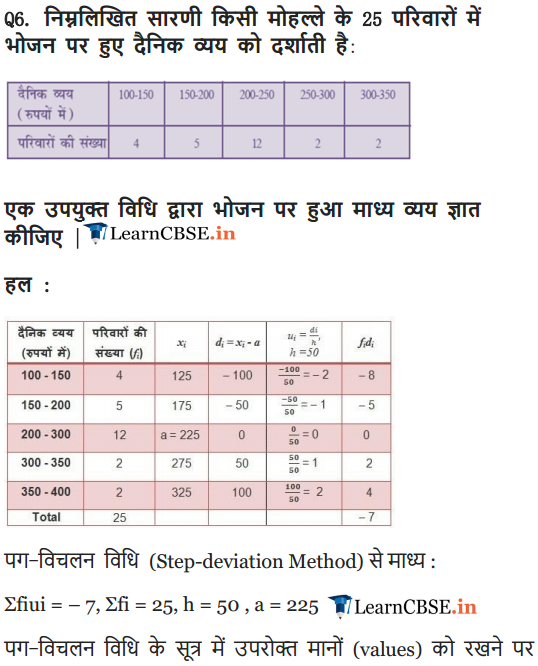
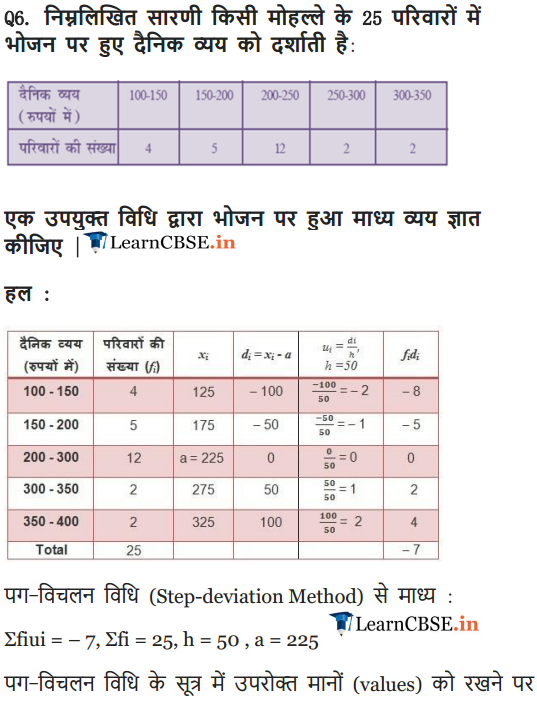
Ex 14.1 Class 10 Maths Question 6.
The table below shows the daily expenditure on food of 25 households in a locality.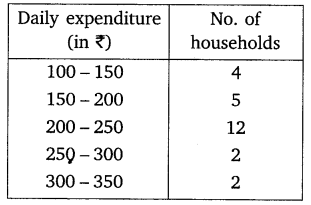

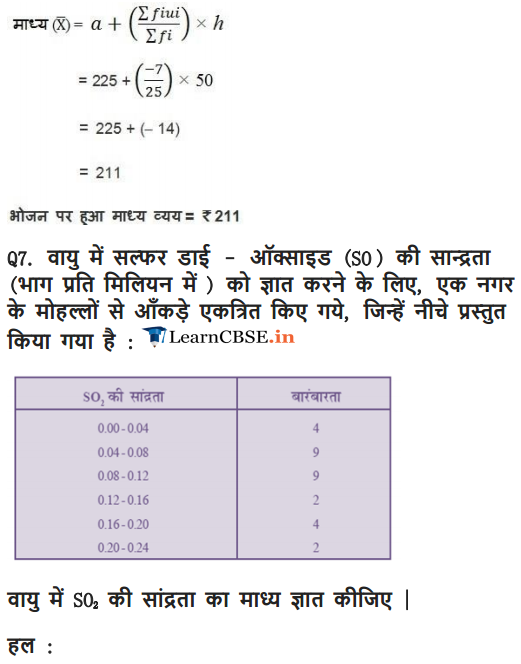
Find the mean daily expenditure on food by a suitable method.
Solution:

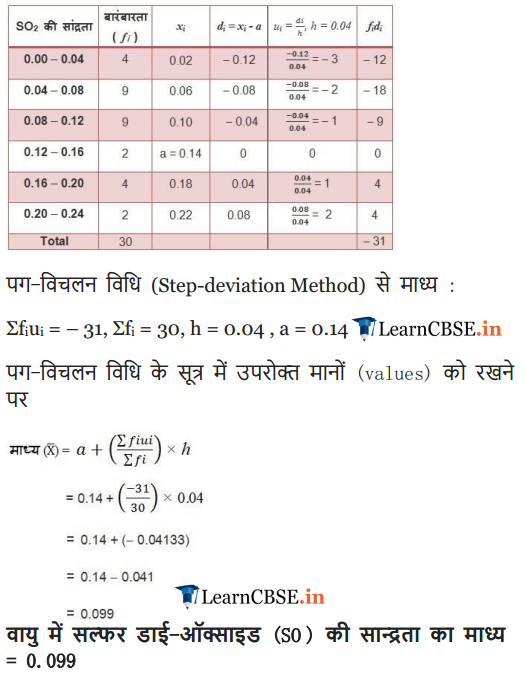
Ex 14.1 Class 10 Maths Question 7.
To find out the concentration of SO2 in the air (in parts per million, i.e. ppm), the data was collected for 30 localities in a certain city and is presented below: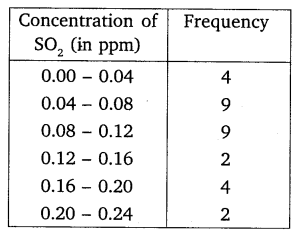

Find the mean concentration of SO2 in the air.
Solution: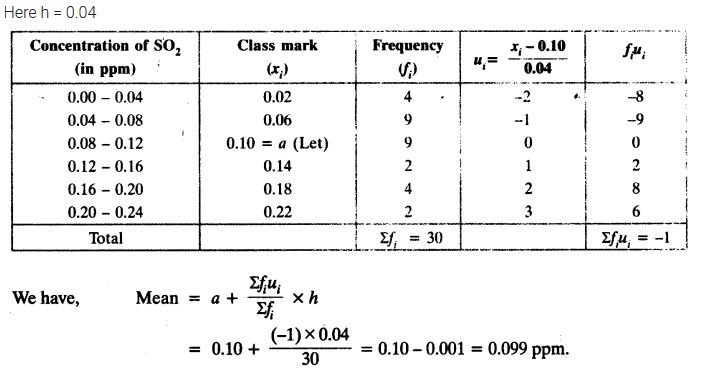

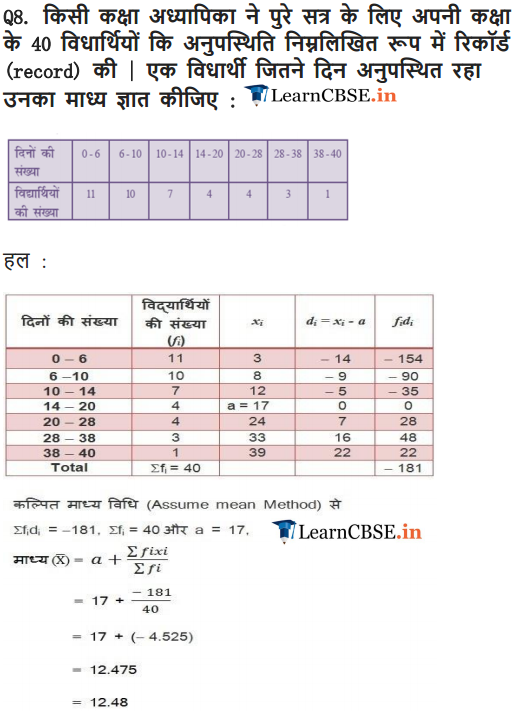
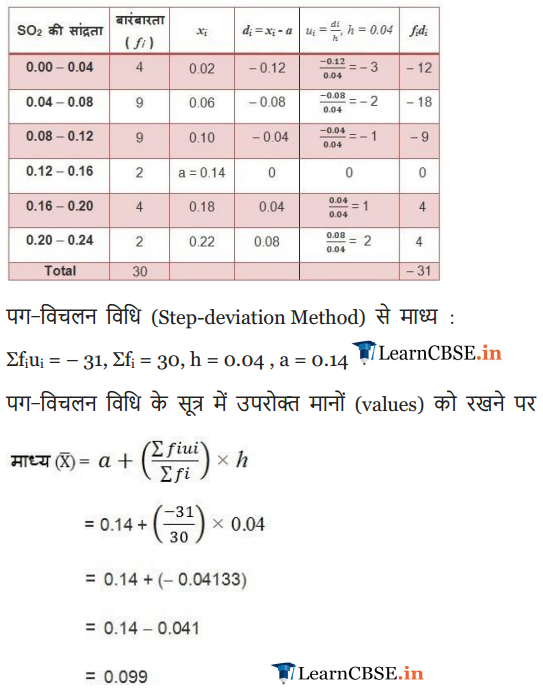
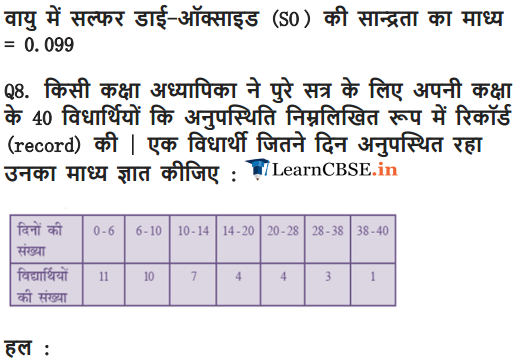
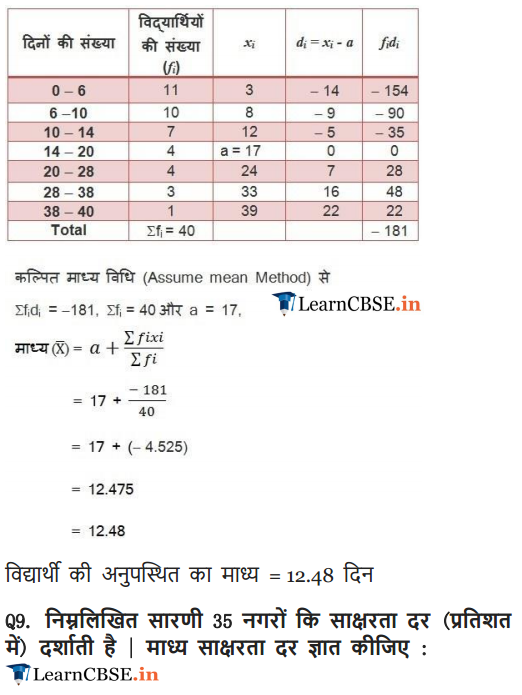
Ex 14.1 Class 10 Maths Question 8.
A class teacher has the following absentee record of 40 students of a class for the whole term. Find the mean number of days a student was absent.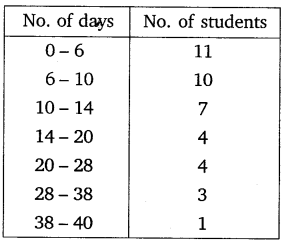

Solution: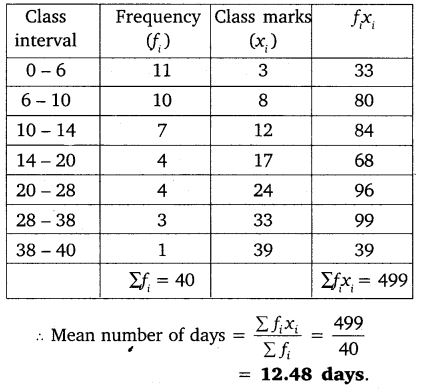

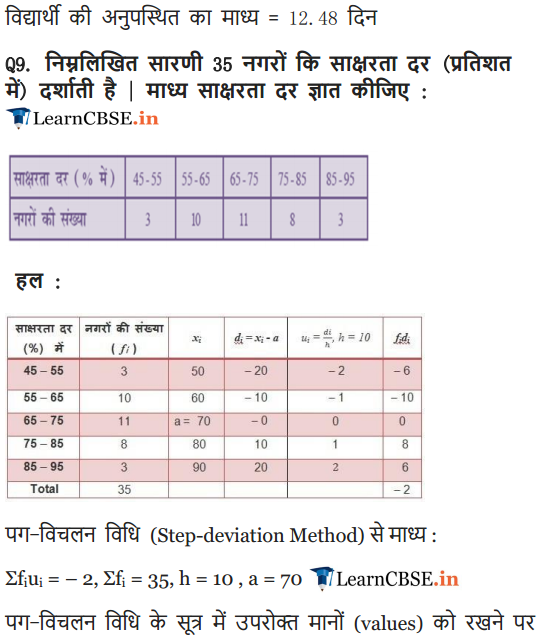
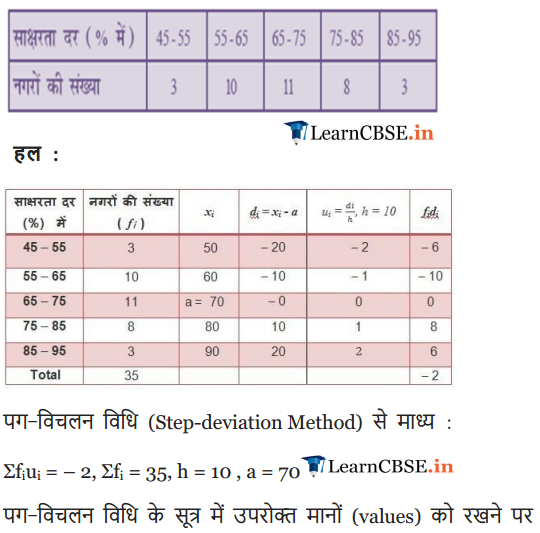
Ex 14.1 Class 10 Maths Question 9.
The following table gives the literacy rate (in percentage) of 35 cities. Find the mean literacy rate.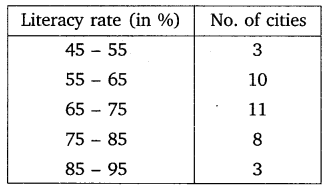

Solution: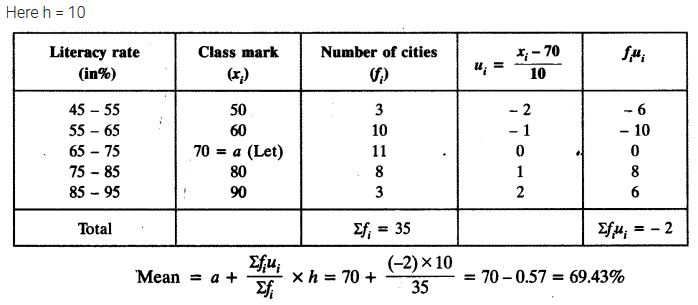

Class 10 Maths Statistics Mind Maps

Basic Terms

Class limits : Suppose mark obtained by all of the students are divided into class intervals 25 – 35, 35 – 45 and so interval on.
In class interval 25 – 35, 25 is called lower class limit and 35 is called upper class limit.
Class size : The difference between upper and lower class limit.
Class mark : It is given by

Ungrouped and Grouped Data

The data obtained in original form are called raw data or ungrouped data.
To put the data in a more condensed form, we make groups of suitable size, and mention the frequency of each group. Such a table is called grouped data.

Mean

For Ungrouped:
Consider ‘n’ observations in ungrouped data as : x1, x2, x3, …. xn. The mean of these observations is:

(i) Direct method: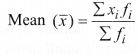

where ‘fi‘ is the frequency corresponding to the class mark ‘xi‘
(ii) Assumed mean method: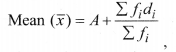

Where A is assumed mean and di = xi – A
(iii) step deviation method: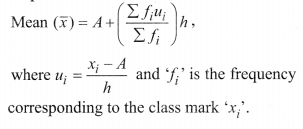

Mode

(i) For Ungrouped Data:
The mode is that observation which occurs most frequently, i.e., an observation with maximum frequency.
(ii) For Grouped Data: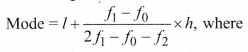

l =lower limit of the modal class,
f1 = frequency of the modal class
f 2 = frequency of the class suceeding the modal class,
h = size of the class interval,
f0 = frequency of the class preceeding the modal class.
The class with the maximum frequency is called modal class.

Median

Median is a measure of central tendency which gives the value of the middle-most observation in the data.
(i) For Ungrouped Data:
Arrange the data in ascending order.
If number of data n is odd, then the median is \(\left(\frac{n+1}{2}\right)^{t h}\) observation.
If number of data n is even, then the median is the average of \(\left(\frac{n}{2}\right)^{t h}\) and \(\left(\frac{n}{2}+1\right)^{t h}\) observations.

(ii) For Grouped Data: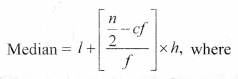

l = lower limit of the median class,
c.f = cumulative frequency of the class proceeding the median class,
f = frequency of the median class,
h = class size,
n = number of observations.
The class whose cumulative frequency is greater than (and nearest to) \(\frac{n}{2}\) is called median class.

Relationship Between Mean, Mode and Median
3 Median = Mode + 2 Mean

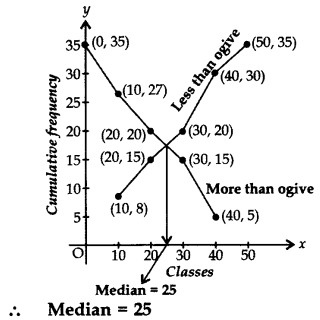
Cumulative Frequency Curve (Ogive)

(i) The smooth free hand curve is formed by joining the points (xi, fi) where x; is the upper limit of a class and f is the corresponding c.f. The curve so obtained is called a cumulative frequency curve, or an ogive of the less than type.
(ii) The smooth free hand curve is formed by joining the points (xi, fi) where Xi is the lower limit of a class and f is the corresponding c.f. The curve so obtained is called a cumulative frequency curve, or an ogive of the more than type.

Median by Graph

(i) Draw the ogive of the less than type and ogive of the more than type on the same axis. The two ogives will intersect each other at a point. From this point, if we draw a perpendicular on the x-axis, the point at which it cuts the x-axis gives us the median.
(ii) Draw the ogive of the less than type, then locate \(\frac{n}{2}\) on the y-axis (n = number of observations).

From this point on y-axis, draw a line parallel to x-axis cutting the less than ogive at a point. From this point draw a perpendicular on the x-axis, the point at which the perpendicular cuts the x-axis gives us the median.

NCERT Solutions for Class 10 Maths Chapter 14 Statistics (Hindi Medium) Ex 14.1

Ex. 14.2

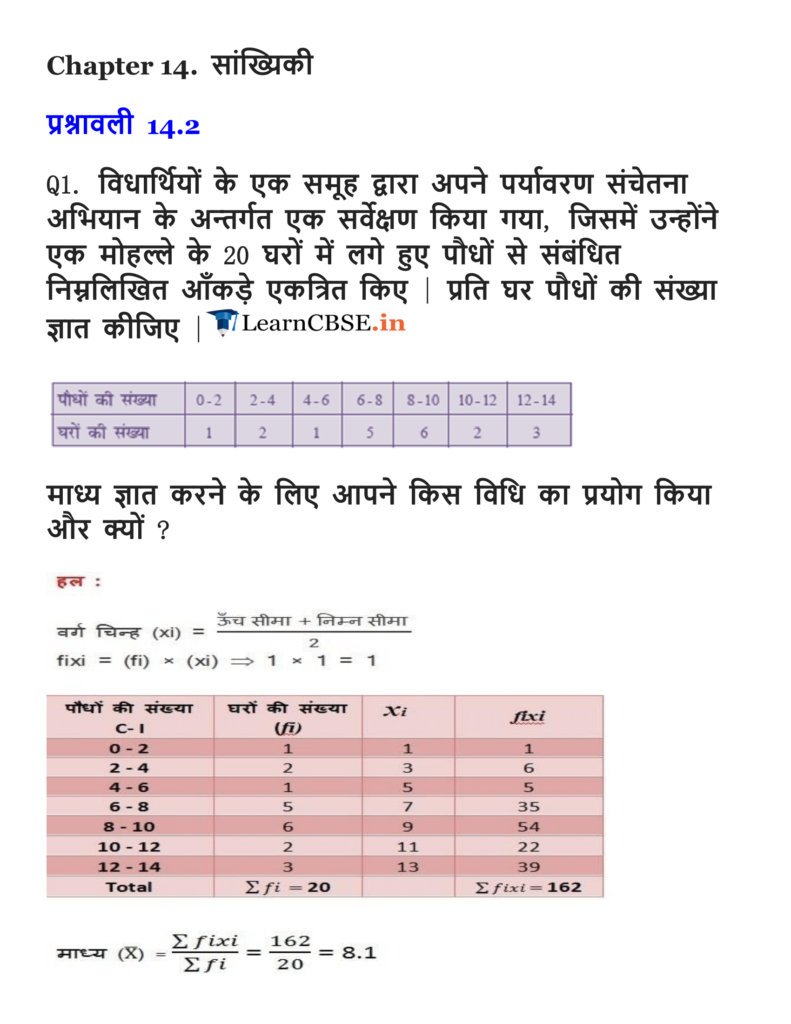
Ex 14.2 Class 10 Maths Question 1.
The following table shows the ages of the patients admitted in a hospital during a year.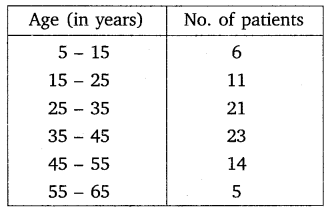

Find the mode and the mean of the data given above. Compare and interpret the two measures of central tendency.
Solution: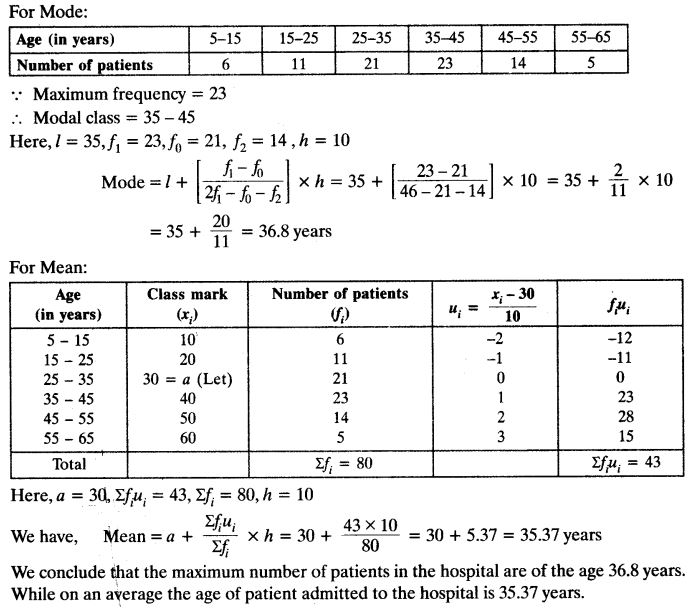

Download NCERT Solutions For Class 10 Maths Chapter 14 Statistics PDF

Ex 14.2 Class 10 Maths Question 2.
The following data gives information on the observed lifetimes (in hours) of 225 electrical components: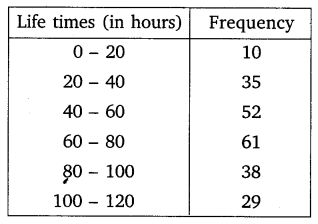

Determine the modal lifetimes of the components.
Solution: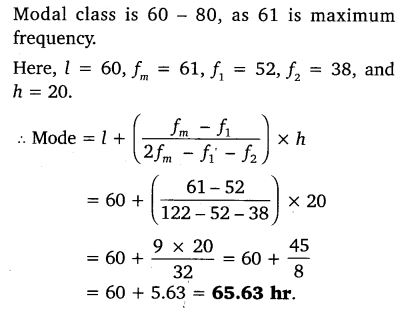

Ex 14.2 Class 10 Maths Question 3.
The following data gives the distribution of total monthly household expenditure of 200 families of a village. Find the modal monthly expenditure of the families. Also, find the mean monthly expenditure: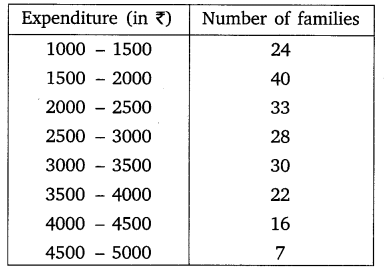

Solution: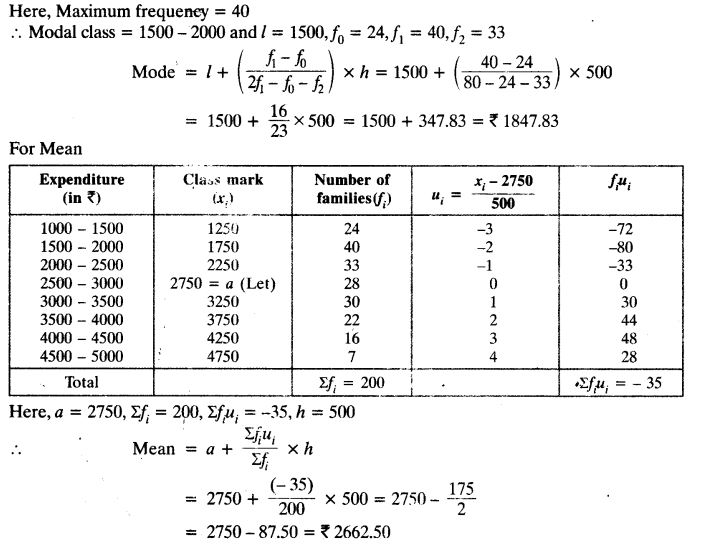

Ex 14.2 Class 10 Maths Question 4.
The following distribution gives the state-wise teacher- student ratio in higher secondary schools of India. Find the mode and mean of this data. Interpret the two measures.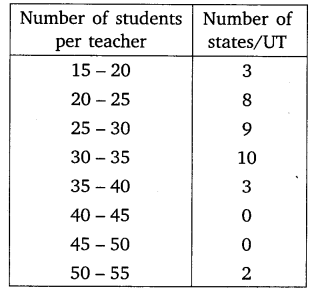

Solution: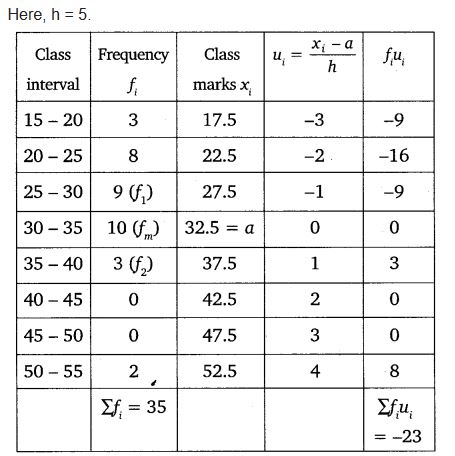

Ex 14.2 Class 10 Maths Question 5.
The given distribution shows the number of runs scored by some top batsmen of the world in one-day international cricket matches.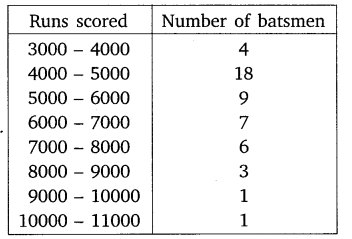

Find the mode of the data.
Solution: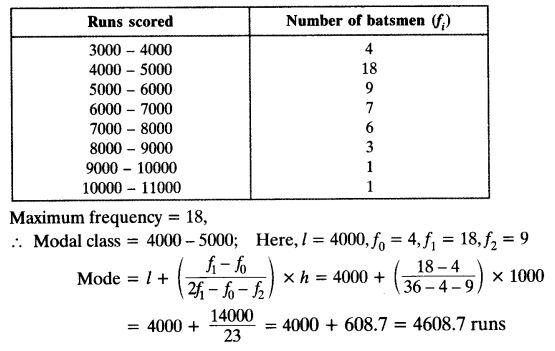

Ex 14.2 Class 10 Maths Question 6.
A student noted the number of cars passing through a spot on a road for 100 periods each of 3 minutes and summarised it in the table given below. Find the mode of the data: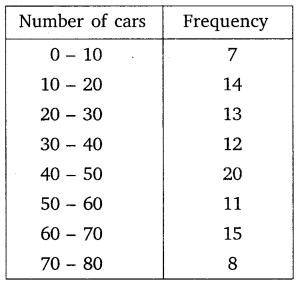

Solution: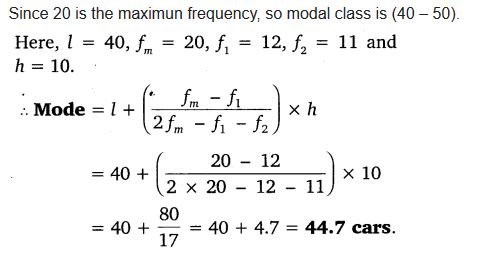

NCERT Solutions for Class 10 Maths Chapter 14 Statistics (Hindi Medium) Ex 14.2

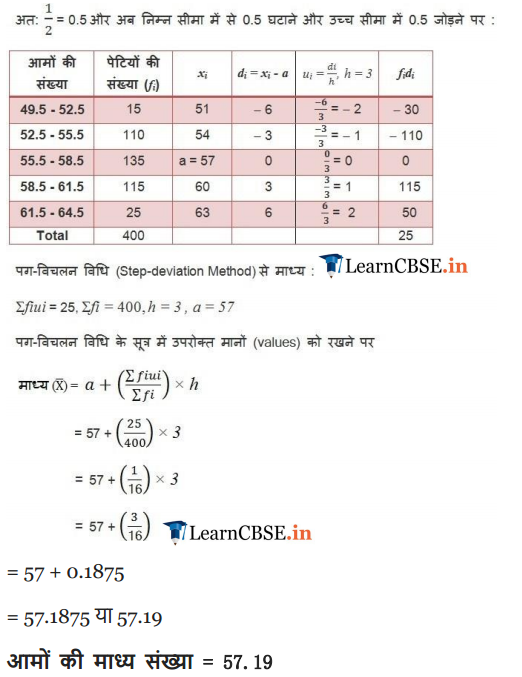
Ex 14.3

Ex 14.3 Class 10 Maths Question 1.
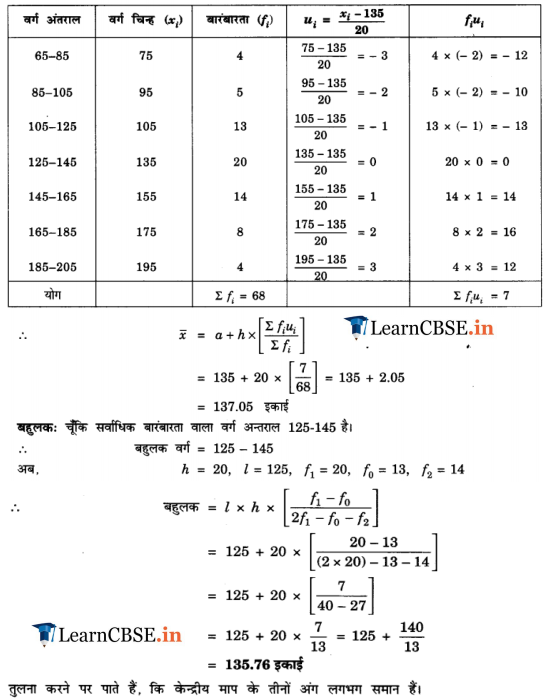
The following frequency distribution gives the monthly consumption of electricity of 68 consumers of a locality. Find the median, mean and mode of the data and compare them.

Solution: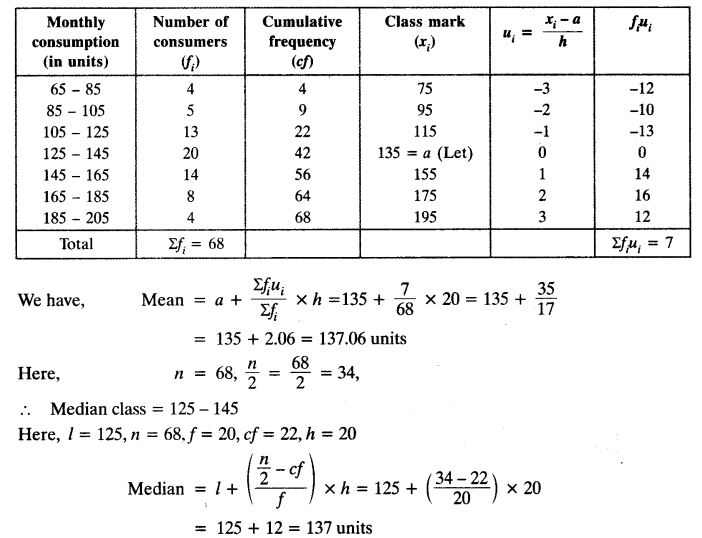

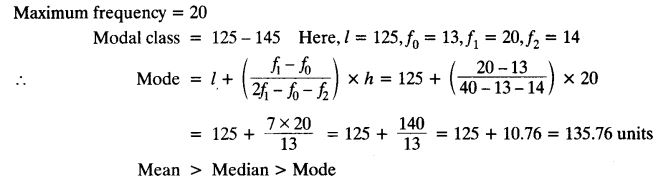
Ex 14.3 Class 10 Maths Question 2.

If the median of the distribution given below is 28.5, find the values of x and y.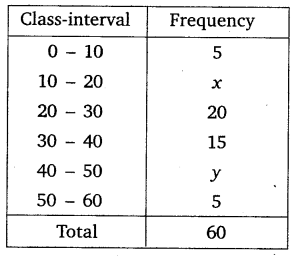

Solution: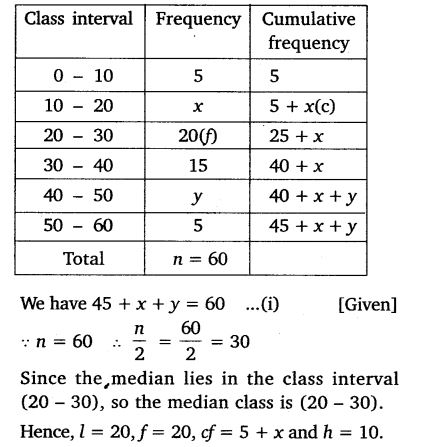

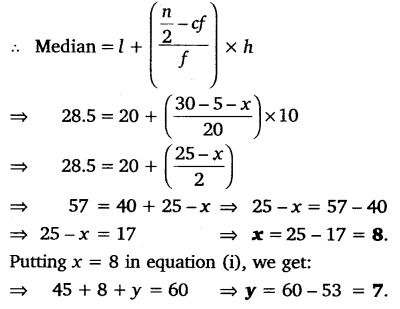
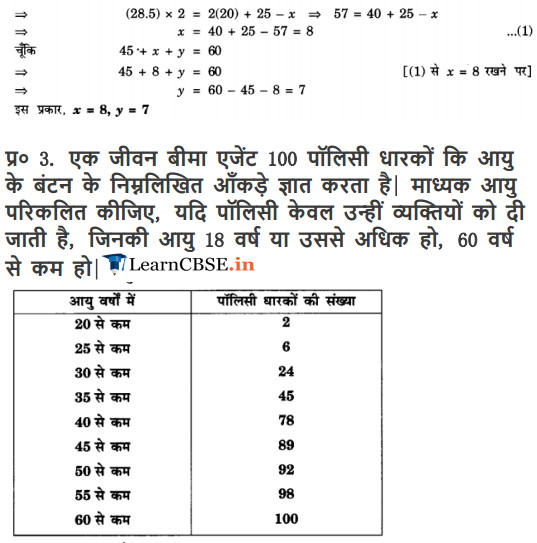
Ex 14.3 Class 10 Maths Question 3.
A life insurance agent found the following data for distribution of ages of 100 policy holders. Calculate the median age, if policies are given only to persons having age 18 years onwards but less than 60 years.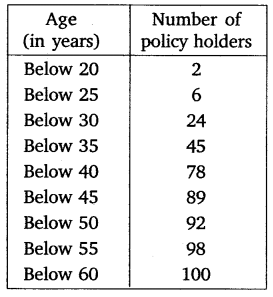

Solution: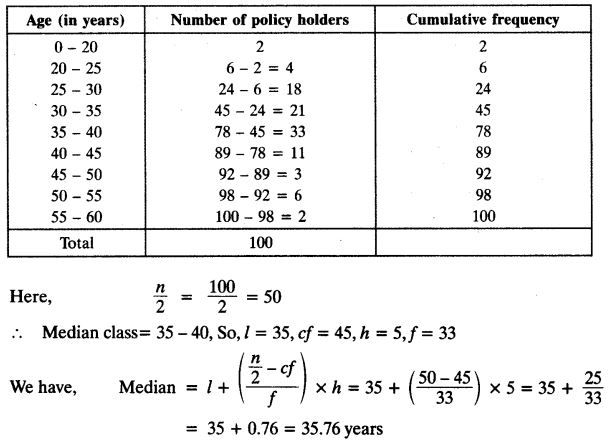

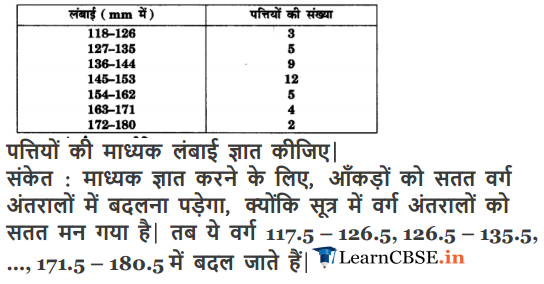
Ex 14.3 Class 10 Maths Question 4.
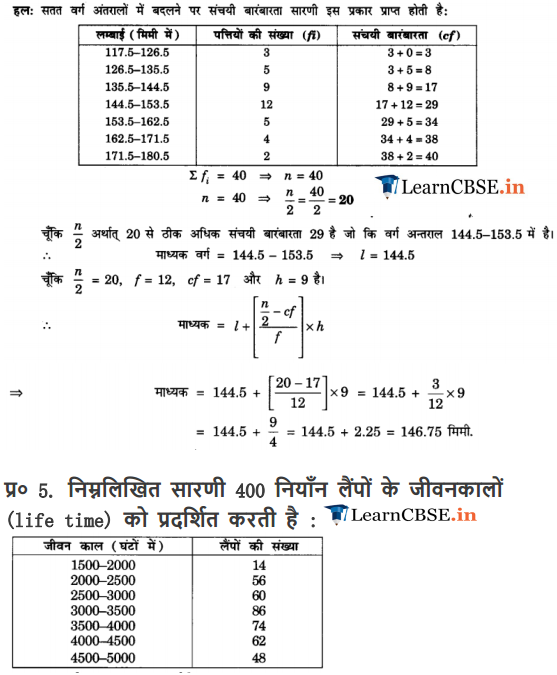
The lengths of 40 leaves of a plant are measured correct to nearest millimetre, and the data obtained is represented in the following table: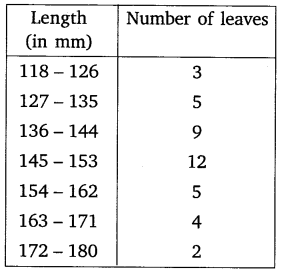

Find the median length of the leaves.
Solution:

Ex 14.3 Class 10 Maths Question 5.
The following table gives the distribution of the lifetime of 400 neon lamps: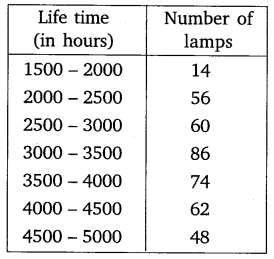

Find the median lifetime of a lamp.
Solution:

Ex 14.3 Class 10 Maths Question 6.
100 surnames were randomly picked up from a local telephone directory and the frequency distribution of the number of letters in the English alphabet in the surnames was obtained as follows:

Determine the median number of letters in the surnames. Find the mean number of letters in the surnames. Also, find the modal size of the surnames.
Solution: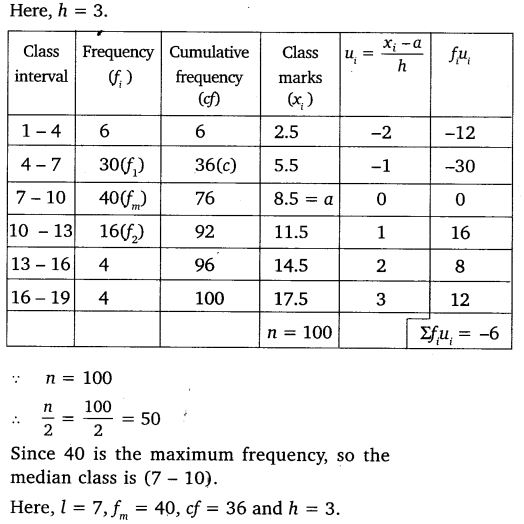

Ex 14.3 Class 10 Maths Question 7.
The distribution below gives the weight of 30 students of a class. Find the median weight of the students.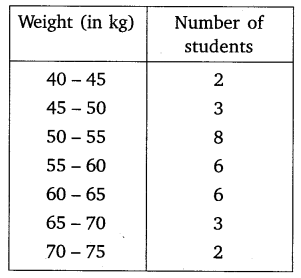

Solution:

NCERT Solutions for Class 10 Maths Chapter 14 Statistics (Hindi Medium) Ex 14.2

Ex 14.4

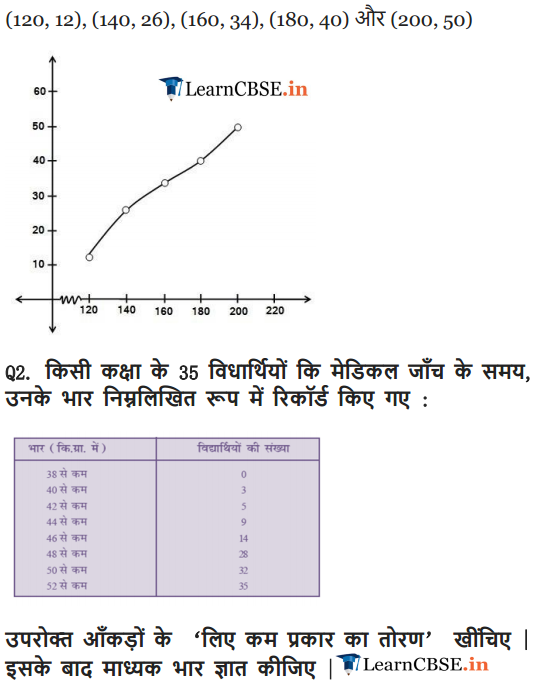
Ex 14.4 Class 10 Maths Question 1.
The following distribution gives the daily income of 50 workers of a factory.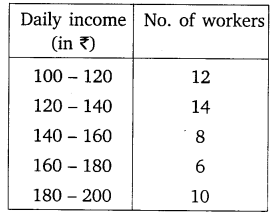

Convert the distribution above to a less than type cumulative frequency distribution, and draw its ogive.
Solution:

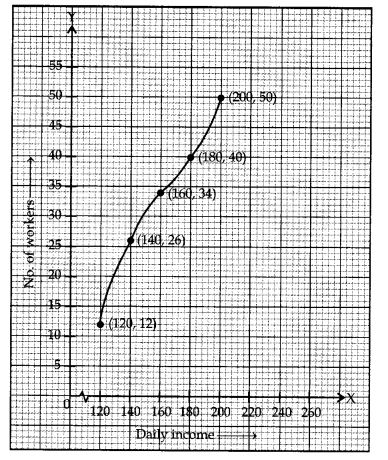
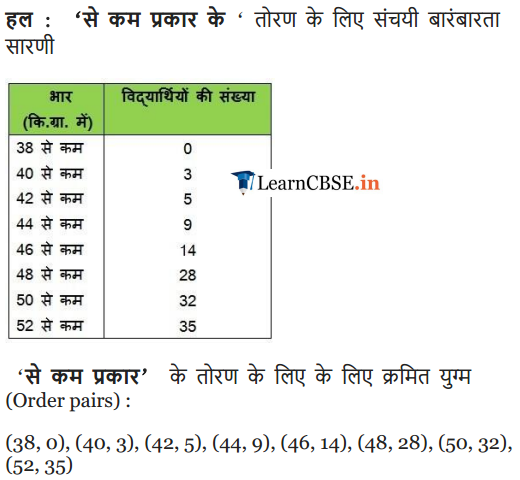
Ex 14.4 Class 10 Maths Question 2.

During the medical check-up of 35 students of a class, their weights were recorded as follows: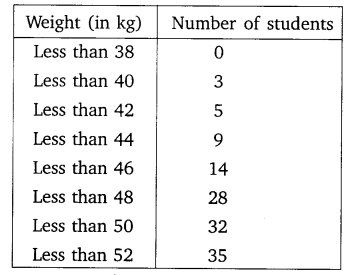

Draw a less than type ogive for the given data. Hence obtain the median weight from the graph and verify the result by using the formula.
Solution: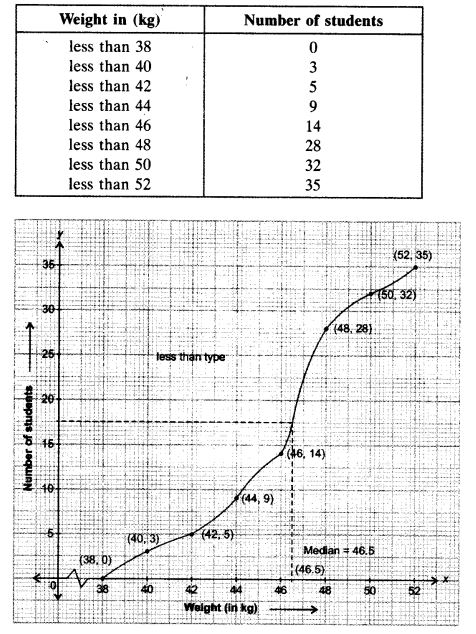

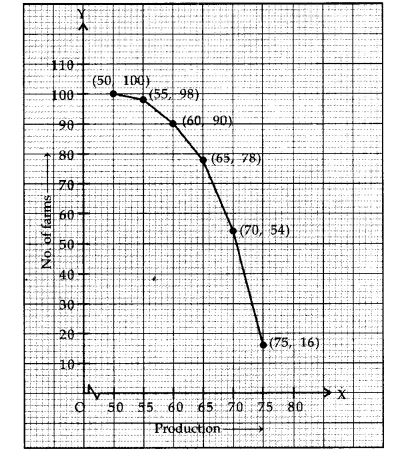
Ex 14.4 Class 10 Maths Question 3.
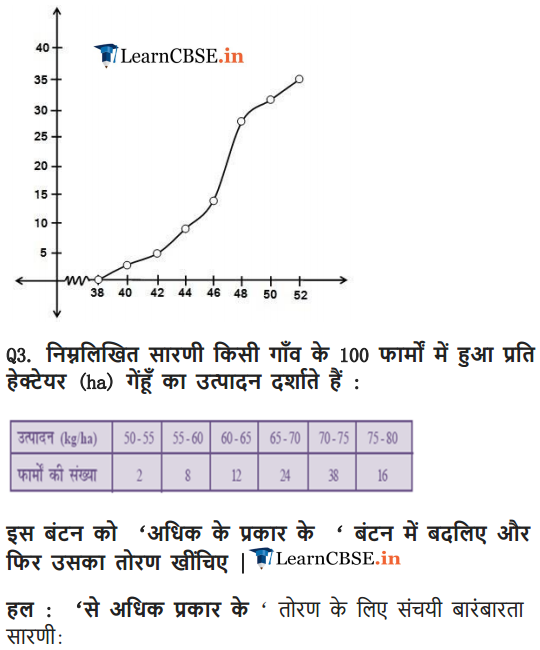
The following table gives production yield per hectare of wheat of 100 farms of a village.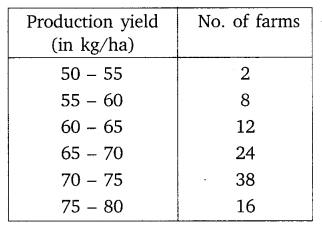

Change the distribution to a more than type distribution, and draw its ogive.
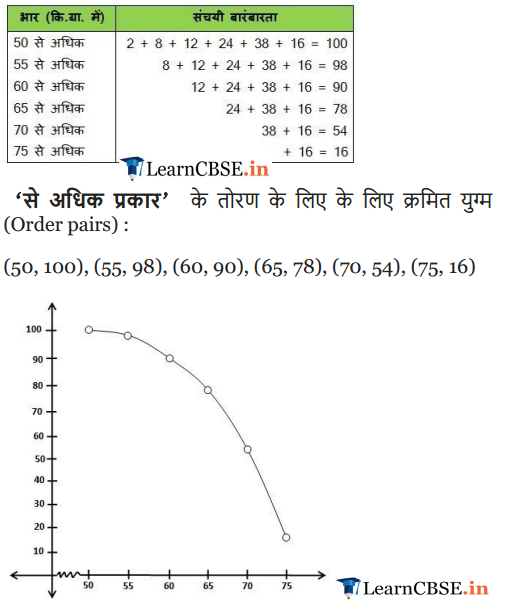
Solution: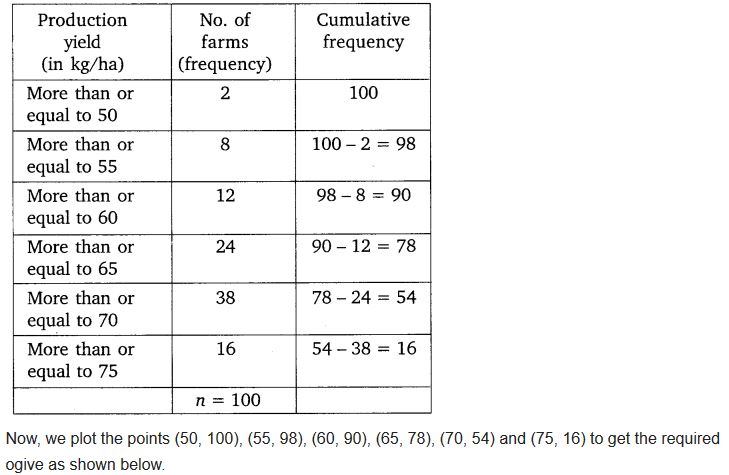

NCERT Solutions for Class 10 Maths Chapter 14 Statistics (Hindi Medium) Ex 14.4

Statistics Class 10 Extra Questions Very Short Answer Type

Question 1.
Find the median of arranged series of an even number of n terms.
Answer:
We know that if n = Even
then Median = (n)th term +(n+1)th term 2

Question 2.
Find the median class of the following data:

Marks obtained	Frequency
0-10	8
10-20	10
20-30	12
30-40	22
40-50	30
50-60	18

Answer: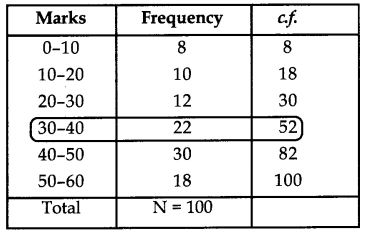

∴ N2=1002 = 50

Looking in the table c.f. just greater than 50 is 52.
∴ Median class = Class corresponding to 52 = 30 – 40.

Question 3.
Find the class marks of classes 10-25 and 35-55.
Answer:
Class mark of 10-25 = 10+252=352 = 17.5
Class mark of 35-55 = 35+552=902 = 45

Question 4.
The point of intersection of two ogives for a distribution is given by (23.7,40.5). What is the median?
Answer:
x-coordination of point of intersection of two ogives give 23.7.
∴ Median = 23.7

Question 5.
If mode = 400 and median = 500, find mean.
Answer:
Mean = Mode + 32 (Median – Mode)
= 400 + 32 (500 – 400)
= 400 + 150
= 550

Question 6.
What is the modal class of the following distribution?

Answer:
The highest frequecny 38 corresponds to 30-40.
∴ The modal class is 30-40.

Question 7.
If the mode of the following data is 7, then find the value of k.
2, 4, 6, 7, 5, 6, 10, 6, 7, 2k + 1, 9, 7, 13
Answer:
There are two entries which occur 3 times each which are 6 and 7.
For 7 to be mode
2k + 1 = 7
k = 62 = 3

Question 8.
The mean of 6 numbers is 16 with the removal of a number the mean of remaining numbers is 17. Find the removed number.
Answer:
Let xd be the sixth number to be remove and x1 x2, …,x5 be remaining 5 numbers.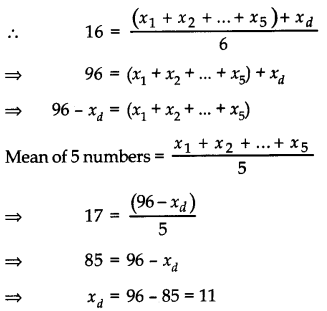

Statistics Class 10 Extra Questions Short Answer Type-1

Question 1.
Age of pumps manufactured by a company are given in the following distribution table.

Age (in years)	No. of Pumps
0-1	12
1-2	18
2-3	45
3-4	23
4-5	12
5-6	08
6-7	04

Calculate the modal age of pumps. [CBSE 2016]
Answer:
Maximum frequency is 45 and it corresponds to the class interval 2-3
∴ Modal class = 2 – 3
So, l = 2; fi = 45; f0 = 18, f2 = 23 and h = 1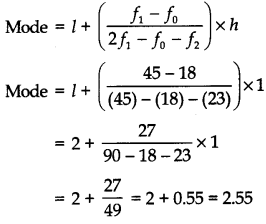

Question 2.
The mean of following frequency distribution is 70. Find the missing frequency x.

CL	Frequency
0-20	5
20-40	8
40-60	21
60-80	12
80-100	x
100-120	8

Answer: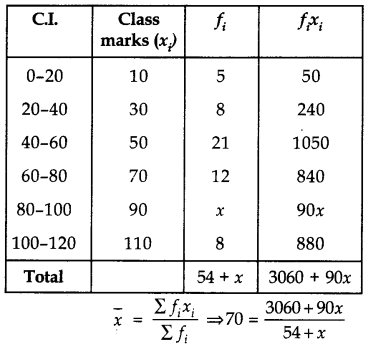

⇒ 3780 + 70x = 3060 + 90x
⇒ 720 = 20x
⇒ x = 72020 = 36

Question 3.
The mean of 11 numbers is 35. If mean of first 6 numbers is 32 and that of last 6 numbers is 37, find 6th number.
Answer:

⇒ x6 + x7 + ……… + x11 = 37 × 6 = 222 ………..(iii)
(ii) and (iii)

⇒ (x1 + x2 + …….. + x6) + (x6 + …….. + x11) = 192 + 222
⇒ x6 + (x1 + x2 + ………. + x11) = 414
⇒ x6 + 385 = 414
⇒ x6 = 414 – 385 = 29 (∵ of (i))

Question 4.
If a variable x takes discrete value x + 4, x – 72, x – 52, x – 2, x + 12, x + 5, x – 3, x – 12, find its median.
Answer:
Arranging the data in ascending order
x – 72, x – 3, x – 52, x – 2, x – 12, x + 12, x + 4, x + 5
Here, N = 8 (even)

Question 5.
Find the mode of the following data:

Height (in cm)	No. of toys
0-10	6
10-20	10
20-30	12
30-40	32
40-50	20

Answer:
Modal class = 30 – 40
l = 30
f1 = 32, f0 = 12, f2 = 20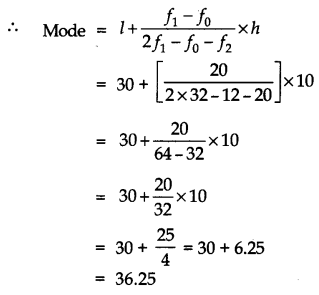

Question 6.
Find median of the following data:

Answer:
Here data is not in ascending order so we first arrange it in ascending order and then append a cumulative frequency column.

xi	fi	cf
15	3	3
21	5	8
27	6	14
30	7	21
35	8	29
		N = 29

Here N = 29, which is odd
∴ Medium = (N+12)th  observation
= (29+12)th  = 15th observation
Since, 15th observation lie in the cumulative frequency 21 for which corresponding observation is 30.
∴ Median = 30

Question 7.
The mean of 9 items is 15. If one more item is added to this series, the mean becomes 16. Find the value of the 10th item.
Answer:

Question 8.
In a school 85 boys and 35 girls appeared in a public examination. The mean marks of boys was found to be 40% whereas the mean marks of girls was 60%. Determine the average marks percentage of the school.
Answer:
Assuming the maximum marks to be 100.
Mean marks of boys (XB ) = 40
and mean marks of girls (XG ) = 60
Also no. of boys (nB) = 85
and no. of girls (nG) = 35

Question 9.
Construct a more than cumulative frequency distribution table for the given data:

Class interval	Frequency
50-60	13
60-70	15
70-80	17
80-90	21
90-100	23
100-110	19

Answer:

Question 10.
Find the median of following given data:

X	f
6	9
7	12
5	8
2	13
10	11
9	14
3	7

Answer: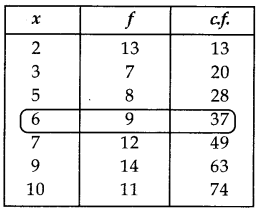

N2=742 = 37
⇒ Median = 6.

Question 11.
Write a frequency distribution table for the following data:

Marks	No. of student
Above 0	30
Above 10	28
Above 20	21
Above 30	15
Above 40	10
Above 50	0

Answer:

Marks	No. of students
0-10	30 – 28 = 2
10-20	28 – 21 = 7
20-30	21 – 15 = 6
30-40	15 – 10 = 5
40-50	10-0 = 10
Total	30

Question 12.
The length of 42 leaves of a plant are measured correct up to nearest millimetre and the data is as under:

Length (in mm)	Number of leaves
118-126	4
126-134	5
134-142	10
142-150	14
150-158	4
158-166	5

Find the modal length of a leave.
Answer:
Since, the maximum number of leaves is 14, therefore modal class 142-150, l = 142, h = 8, f1 = 14, f0 = 10, f2 = 4
Mode = l + f1−f02f1−f0−f2 × h
= 142 + 14−102×14−10−4 × 8
= 142 + 414 × 8 = 144.29

Question 13.
Find the mean of the following frequency distributions by the direct method: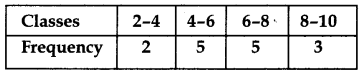

Answer: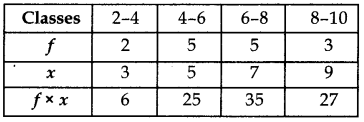

Σf × x = 93, Σf = 15
Mean = ΣfxΣf=9315 = 6.2

Statistics Class 10 Extra Questions Short Answer Type-2

Question 1.
For Uttarakhand flood victims, money donated by teachers of a school is shown in the following frequency distribution:

Money donated (in ₹)	No. of Teachers
500-700	4
700-900	3
900-1100	18
1100-1300	2
1300-1500	3

Find mean and median for this data. [CBSE Delhi 2016]
Answer:
Mean: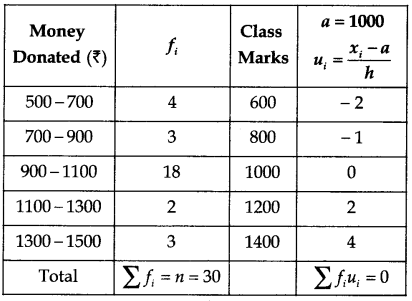

From the above data, Assumed mean (a) = 1000
Width of the class (h) = 200
∴ ū = ∑fiui∑fi=030 = 0

Mean (x̄) = a + hū
= 1000 + 100 × 0
= 1000

Median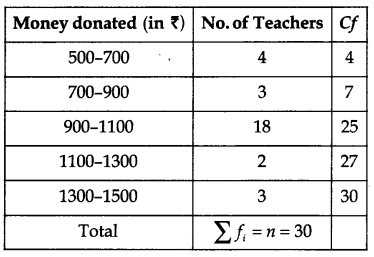

Here, Σfi = n = 30, then n2=302 =15
which lies in interval 900 – 1100.
Median class = 900 – 1100
l = 900, n = 30, f = 18, cf = 7 and h = 200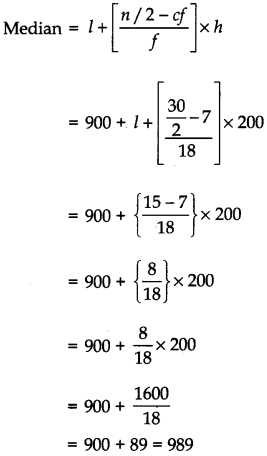

Question 2.
The table below shows the salaries of 280 persons:

Salary (In thousand ₹)	No. of Persons
5-10	49
10 – 15	133
15 – 20	63
20 – 25	15
25 – 30	6
30 – 35	7
35 – 40	4
40 – 45	2
45-50	1

Calculate the median salary of the data.
Answer: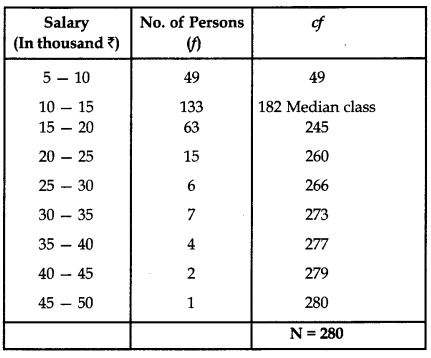

N2=2802 = 140
Median class is 10 – 15
Median = l + hf(N2−C)
= 10 + 5133(140 – 49)
= 10 + 5×91133 = 13.42
Median salary is ₹ 13.42 thousand or ₹ 13420 (approx).

Question 3.
The mean of the following frequency distribution is 62.8 and the sum of all frequencies is 50. Compute the missing frequencies f1 and f2.

Class	Frequency
0-20	5
20-40	A
40-60	10
60-80	A
80-100	7
100-120	8
Total	50

Answer: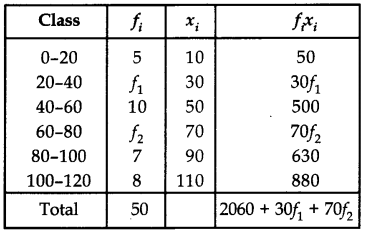

Now 50 = 5 + f1 + 10 + f2 + 7 + 8
⇒ 50 = 30 + f1 + f2
⇒ f1 + f2 = 20 ……….(i)

Also, Mean = ΣfixiΣfi
⇒ 62.8 = 2060+30f1+70f250
3140 = 2060 + 30f1 + 70f2
3f1 + 7f2 = 108

Solving (i) and (ii), we get
f1 = 8 and f2 = 12

Question 4.
Find the missing frequecny (x) of the following data if its mode is ₹240.
Answer:
Here mode is given to be ₹ 240, which lies between 200 and 300. Therefore, modal class is 200 – 300
We have l = 200, f1 = 270, f0 = 230, f2 = x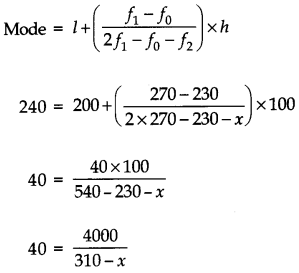

12400 – 40x = 4000
40x = 12400 – 4000
40x = 8400
x = 210

Question 5.
Find the missing frequency f1 and f2 if mean of 50 observations is 38.2.

Class interval	Frequency
0-10	4
10-20	4
20-30	f1
30-40	10
40-50	f2
50-60	8
60-70	5

Answer:

Class interval	Frequency fi	xi	fixi
0-10	4	5	20
10-20	4	15	60
20-30	f1	25	25f1
30-40	10	35	350
40-50	f2	45	45f2
50-60	8	55	440
60-70	5	65	325
Total	50		1195 + 25f1 + 45f2

Σfi = 31 + f1 + f2
31 + f1 + f2
f1 + f2 = 19 ………..(i)
38.2 = 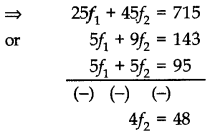1195+25f1+45f250

⇒ f2 = 12

Putting f2 = 12 in (i)
⇒ f1 = 7

Question 6.
Find the mean of the following frequency distribution by short cut method:

Answer: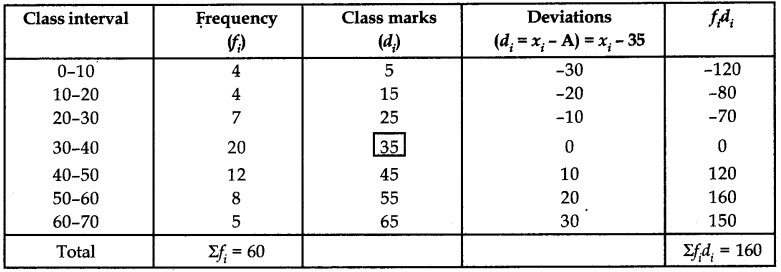

Let assumed mean (A) be 35.
∴ Mean (x̄) = A + ΣfidiΣfi = 35 + 16060
= 35 + 2.67
= 37.67

Question 7.
Form a grouped frequency distribution and calculate the median.

Answer:
We first convert the given data into grouped frequency distribution and then append a cumulative frequency column as given below.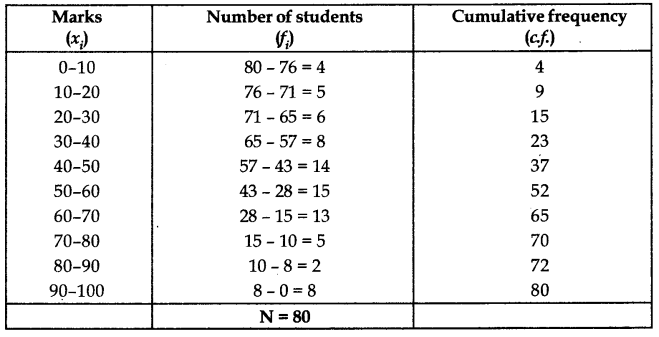

Here N = 80 ⇒ N2=802 = 40
Cumulative frequency just greater than or equal to 40 is 52 which corresponds to 50 – 60.
Median class = 50-60
The lower limit of the median class (l) – 50
The cumulative frequency of the class preceding the median class (cf) = 37
The frequency of the median class (50 – 60) (f) = 15
The width of the median class (h) = 10
∴ Median = l + (N2−cf)f × h
= 50 + (40−3715) × 10
= 50 + 3015 = 50 + 2 = 52

Question 8.
The mean of the following distribution is 18. [CBSE 2018]

Answer:
Let the assumed mean (a) = 18
∵ h = 2
∴ ui = xi−182
∴ We have the following table:

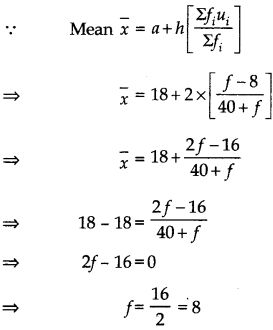
Question 9.
Find the mode of the following distribution of marks obtained by the students in an examination:

Given the mean of the above distribution is 53, using emperical relationship estimate the value of its median.
Answer:
Sol. Modal class is 60-80 (Class corresponding to maximum frequency)
∴ Mode = l + (f1−f02f1−f0−f2) × h
= 60 + (29−2158−21−17) × 20 = 68
So, the mode marks is 68.
Empirical relationship between the three measures of central tendencies is:
3 Median = Mode + 2 mean
3 Median = 68 + 2 × 53
Median = 58 marks

Statistics Class 10 Extra Questions Long Answer Type 1

Question 1.
If the median of the following frequency distribution is 32.5. Find the values of f1 and f2. [CBSE 2019]

Or
The marks obtained by 100 students of a class in an examination are given below.

Marks	No. of Students
0-5	2
5-10	5
10-15	6
15-20	8
20-25	10
25-30	25
30-35	20
35-40	18
40-45	4
45-50	2

Draw ‘a less than’ type cumulative frequency curves (Ogive). Hence find median.
Answer:

Median = 32.5
∴ Median class is 30-40
Median = l+(N2−C)f × h
Here, l = 30, N = 40, C = 14 + f1
f1 = 12, h = 10
∴ 32.5 = 30 + 1012(20 – 14 – f1)
⇒ f1 = 3
Also, 31 + f1 + f2 = 40
Putting f1 = 3 in (2)
⇒ f2 = 6

Or

Next we plot the points of last column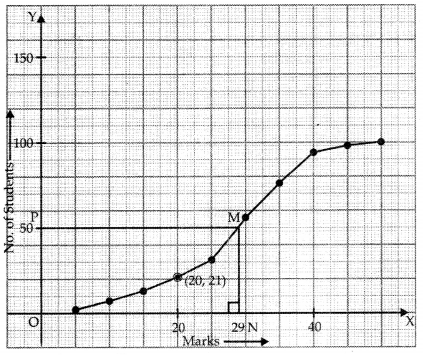

Mark point ‘F corresponding to N2 = 50.
Draw PM ∥ x-axis to cut Ogive at M.
Draw MN ⊥ x-axis to cut it at N.
Since, N is (29, 0)
∴ Median = 29.

Question 2.
If the mean of the following frequency distribution is 62.8, then find the missing frequency x: [CBSE 2019(C)]

Class	Frequency
0-20	5
20-40	8
40-60	X
60-80	12
80-100	7
100-120	8

Answer: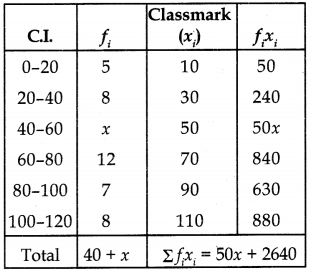

Now, mean (x̄) = ∑fixi∑fi
62.8 = (50x+2640)40+x
⇒ 62.8 (40 + x) = 50x + 2640
⇒ 2512 + 62.8x = 50x + 2640
⇒ 12.8x = 128
⇒ x = 12812.8 = 10

Question 3.
Find the mean, mode and median of the following data:

Classes	Frequency (f)
0-10	3
10-20	8
20-30	10
30-40	15
40-50	7
50-60	4
60-70	3

Answer:
We prepare the table which serves all three purposes of getting mean, median and mode as given below: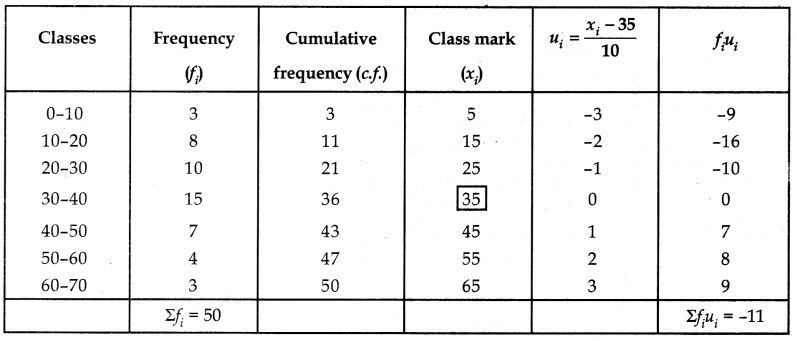

(i) Mean: Let assumed mean (A) be 35.
Mean = A + (ΣfiuiΣfi×h)
= 35 + (−1150×10)
= 35 – 2.2 = 32.8

(ii) Mode: As maximum frequency is 15.
∴ Mode classes is 30-40.
Thus f1 = 15, f0 = 10 , f2 = 7
Mode = l + (f1−f02f1−f0−f2) × h
= 30 + (15−1030−10−7) × 10
= 30 + 5013 = 30 + 3.85 = 33.85

(iii) Median: Here N = 50 ⇒ N2 = 25
The cumulative frequency just greater than 25 is 36 and the corresponding class is 30-40.
∴ Median class = 30-40, l = 30, cf = 21, f = 15
Now, Median = l + (N2−cff) × h
= 30 + (25−2115) × 10
= 30 + 4015 = 30 + 2.67 = 32.67

Question 4.
During the medical check up of 35 students of a class, their weights were recorded as follows: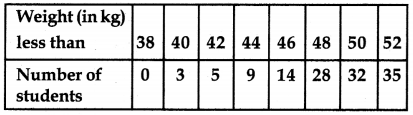

Draw a less than type ogive for the given data. Hence obtain the median weight from the graph and verify by using the formula.
Answer:
Here data is already tabulated as less than cumulative frequency table.
So, we have to just plot the ordered pairs (38,0), (40,3), (42,5), (44,9), (46,14), (48,28), (50,32) and (52,35) join them by free hand to get the less than type ogive as shown below:
Here 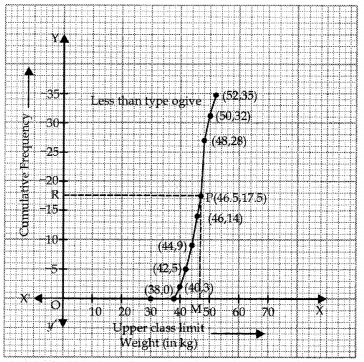N2=352 = 17.5. So we mark a point R on y-axis such that OR = 17.5

Draw a line RP parallel to x-axis as shown in graph which meets the ogive at point P.
Draw PM ⊥ OX
Now Since OM = 46.5
∴ Median = 46.5
Verification: For calculation median by using formula we first convert the given cumulative frequency table to continuous grouped frequency distribution as given below: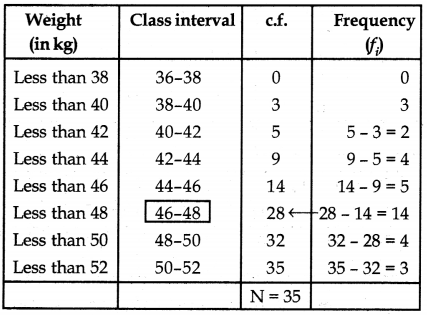

Question 5.
Draw ‘Less than’ and ‘more than’ ogives for the following distribution and hence find its median.

Class	Frequency
20-30	8
30-40	12
40-50	24
50-60	6
60-70	10
70-80	15
80-90	25

Answer:

‘Less than ogive’
‘Less than’	c.f	Ordered pairs
20	0	(20, 0)
30	8	(30, 8)
40	20	(40, 20)
50	44	(50, 44)
60	50	(60, 50)
70	60	(70, 60)
80	75	(80, 75)
90	100	(90,100)

‘More than ogive’
‘More than’	c.f	Ordered pairs
20	100	(20,100)
30	92	(30, 92)
40	80	(40, 80)
50	56	(50, 56)
60	50	(60,50)
70	40	(70,40)
80	25	(80, 25)
90	0	(90,0)

The ‘less than’ type and ‘more than’ type ogives can be drawn on graph paper as: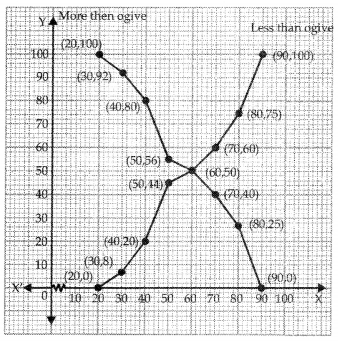

It can be observed that the ‘less than’ type and ‘more than’ type ogives of the given frequency distribution intersect at point P(60, 50). If we draw a perpendicular to the x-axis from point P, then the value on the x-axis is obtained as 60.
Thus, the median of the given data is 60.

Question 6.
Calculate the mode of the following frequency distribution table:

Marks	Number of students
Above 25	52
Above 35	47
Above 45	37
Above 55	17
Above 65	8
Above 75	2
Above 85	0

Answer:

CL	f	c.f
25-35	5	52
35-45	10	47
45-55	20	37
55-65	9	17
65-75	6	8
75-85	2	2

∴ Mode = l + [f1−f02f1−f0−f2] × h
= 45 + (20−10)2×20−10−9 × 10
= 45 + 10021
= 49.76

Question 7.
The following table shows the ages of 100 persons of a locality. Draw less than ogive.

Age (in years)	Number of persons
0-10	5
10-20	15
20-30	20
30-40	23
40-50	17
50-60	11
60-70	9

Answer:

Age (in years)	No. of persons	Ordered pairs
Less than 10	5	(10,5)
Less than 20	20	(20, 20)
Less than 30	40	(30,40)
Less than 40	63	(40, 63)
Less than 50	80	(50, 80)
Less than 60	91	(60, 91)
Less than 70	100	(70,100)

At A(Corresponding to N2 = 50) draw AP ∥x-axis
From P draw PM ⊥x -axis. Abscissa of M is 34.5(approx)
∴ Median = 34.5 (Approx)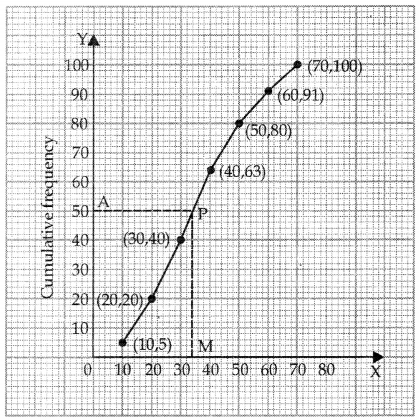

Question 8.
Find the mode, median and mean for the following data: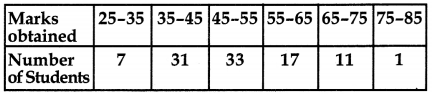

Answer:
Let the assumed mean a = 60. Here h = 10, we have: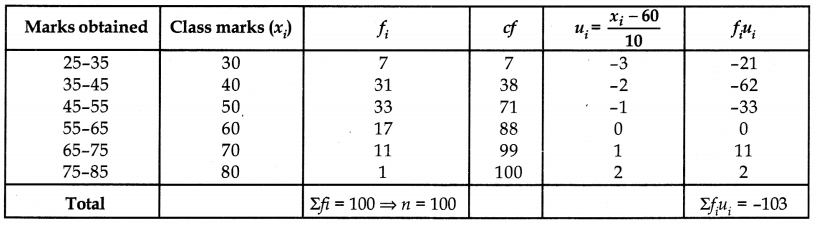


(iii) Mode: Greatest frequency is 33 which corresponds to the class 45-55.
l1 = 45, h = 10
f1 = 33, f2 = 17
f0 = 31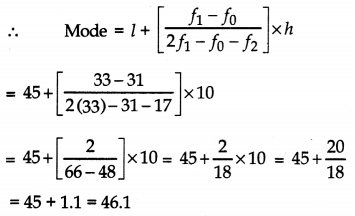

Question 9.
The following frequency distribution shows the distance (in metress) thrown by 68 students in a Javelin throw competition.

Distance (in m)	Number of students
0-10	4
10-20	5
20-30	13
30-40	20
40-50	14
50-60	8
60-70	4

Draw a less than type ogive for the given data and find the median distance thrown using this curve. [CBSE Sample Paper 2017-18)]
Answer:

Less than	Number of Students
10	4
20	9
30	22
40	42
50	56
60	64
70	68

Median distance is value of x that corresponds to
Cumulative frequency N2=672 = 34
Therefore, Median distance = 36 m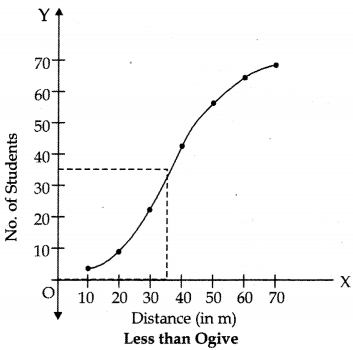

Statistics Class 10 Extra Questions HOTS

Question 1.
Average cost of 5 apples and 2 pineapples is ₹ 250. The average cost of 7 apples and 4 pineapples is ₹ 340. Find the total cost of 24 apples and 12 pineapples.
Answer:
Average cost of 5 apples and 2 pineapples = ₹ 250
⇒ Total cost of 5 apples and 2 pineapples = ₹ (250 × 7)
= ₹ 1750 …(i)
Similarly, total cost of 7 apples and 4 pineapples = (₹ 340 × 11)
= ₹ 3740 …(ii)
(i) and (it)
⇒ Total cost of (5 + 7 = 12) apples and (2 + 4 = 6)
pineapples = ₹ 1750 + ₹ 3740 = ₹ 5490
Thus cost of 24 apples and 12 pineapples = ₹ (5490 × 2) = ₹ 10980

Question 2.
A student finds the average of 10 positive integers. Each integer contains two digits. By mistake, the boy interchanged the digits of one number. Due to this average becomes 1.8 less than the previous one. What was the difference of digits of the number which was wrongly written.
Answer:
Let the sum of 9 correct numbers be ‘A’ and the units and tens place digits of 10th number be x and y respectively.
∴ x̄ = A+(10x+y)10 …….(i)
When digits interchanged for 10th number its value becomes lOx + y.
By the condition, x̄ – 1.8 = A+(10x+y)10
⇒ x = A+(10x+y)10 …(ii)
From (i) and (ii), we get
A+(10y+x)10=A+(10x+y)10 + 1.8
⇒ A + (10x + y) + 18 = A + 10y + x
⇒ 9y – 9x = 18
⇒ y – x = 2
Thus the difference of digits = 2.

Multiple Choice Questions
Choose the correct option out of four given in each of the following:

Question 1.
In the given frequency distribution table, the values of missing frequency a1 and a2 respectively are:

Cl.	Frequency	Cumulative frequency
0-10	5	a3
10-20	a1	12
20-30	9	21
30-40	a2	31
40-50	9	fl4

(a) a1 = 5, a2 = 5
(b) a1 = 7, a2 = 5
(c) a1 = 7, a2 = 10
(d) a1 = 5, a2 = 10
Answer:
(c) a1 = 7, a2 = 10

Question 2.
For a frequency distribution, mean, median and mode are connected by the relation:
(a) Mode = 3 Mean – 2 Median
(b) Mode = 2 Median – 3 Mean
(c) Mode = 3 Median – 2 Mean
(d) Mode = 3 Median + 2 Mean
Answer:
(c) Mode = 3 Median – 2 Mean

Question 3.
The mean of a discrete frequency distribution xi|fi; i = 1, 2, 3, …………. n is given by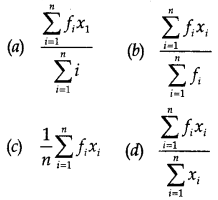

Answer:
(b) ∑ni=1fixi∑ni=1fi

Question 4.
In the formula x̄ = A + ∑fidi∑fi for finding the mean of grouped data d-s are deviations from A of:
(a) lower limits of the classes
(b) upper limits of the classes
(c) mid point of classes
(d) frequencies of the class marks.
Answer:
(c) mid point of classes

Question 5.
Construction of cumulative frequency table is useful in determining the
(a) mean
(b) median
(c) mode
(d) all, mean, mode and median.
Answer:
(b) median

Question 6.
In the formula x̄ = A + ∑fiui∑fi × h, for finding the mean of grouped frequency distribution, ui =
(a) (xi + A)/h
(b) h(xi – A)
(c) (xi – A)/h
(d) (A – xi)/h
Answer:
(c) (xi – A)/h

Question 7.
While computing mean of grouped data, we assume that the frequencies are:
(a) evenly distributed over all classes
(b) centered at the class marks of classes
(c) centered at upper limits of classes
(d) centered at lower limts of classes.
Answer:
(b) centered at the class marks of classes

Question 8.
If xi‘s are the mid points of the class intervals of grouped data, f’is are the corresponding frequencies and x is the mean, then Σfi(xi – x̄) is equal to:
(a) zero
(b) – 1
(c) 1
(d) 2
Answer:
(a) zero

Question 9.
Which of the following is not a measure of central tendency ?
(a) Mean
(b) Median
(c) Mode
(d) Variance
Answer:
(d) Variance

Question 10.
The mean of a set of numbers is x̄. If each number is divided by 3, then the new mean is:
(a) x̄
(b) x̄ + 3
(c) 3x̄
(d) x¯3
Answer:
(d) x¯3

Question 11.
Mean of a set of 8 observations is 10 and 4 is the mean of a set of 7 observations. The mean of the combined set is given by:
(a) 10.8
(b) 7.2
(c) 8.2
(d) 9
Answer:
(d) 9

Question 12.
The mode of a frequency distribution can be determined graphically from:
(a) histogram
(b) frequency polygon
(c) ogive
(d) frequency curve.
Answer:
(a) histogram

Question 13.
The algebraic sum of the deviations of a frequency distribution from its mean is:
(a) always positive
(b) always negative
(c) 0
(d) a non-zero number.
Answer:
(c) 0

Question 14.
The median of a given frequency distribution is found graphically with the help of:
(a) histogram
(b) frequency polygon
(c) frequency curve
(d) ogive.
Answer:
(d) ogive.

Question 15.
What is not true about mode ?
(a) It can be determined graphically
(b) It is the most frequent value
(c) The formula for finding mode is l + (f1−f02f1−f0−f2) × h
(d) None of these.
Answer:
(d) None of these.

Fill in the Blanks

Question 1.
That value of data from which algebraic sum of deviations of each observation vanishes is ____________ of the data.
Answer:
mean

Question 2.
The most frequent value of data is called ____________
Answer:
Mode

Question 3.
Another one word name for mean is ____________
Answer:
Average

Question 4.
If 50% of the observation lies above a value and another 50% alongside or below it, then this value is called as ____________
Answer:
Median

Question 5.
In case of categorical data ____________ is used as measure of central tendency.
Answer:
Mode

Question 6.
To find the mode of a grouped data, the size of the classes is ____________ (uniform/non-uniform)
Answer:
uniform

Question 7.
The class mark of a class interval p-q is ____________
Answer:
p+q2

Question 8.
Two ogives, ‘less than’ type and ‘more than’ type of the same data intersect at the point P. The height of this point P represents ____________
Answer:
Half of total frequency

Question 9.
For a distribution with odd number (n) of observations, median = ____________.
Answer:
(n+12)th observation

Question 10.
For a distribution with even number (n) of observations, median = ____________.
Answer:
Mean of (n2)th  and (n2+1)th  observation

Important Questions for Class 10 Maths Chapter 14 Statistics

Statistics Class 10 Important Questions Very Short Answer (1 Mark)

Question 1.
In a continuous frequency distribution, the median of the data is 21. If each observation is increased by 5, then find the new median. (2015)
Solution:
New median = 21 + 5 = 26

Question 2.
From the following frequency distribution, find the median class: (2015)

Solution: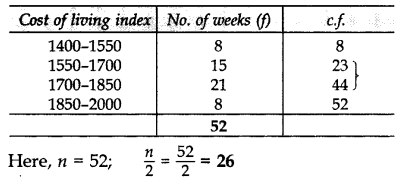

∴ Median class 1700 – 1850.

Question 3.
Consider the following distribution, find the frequency of class 30-40. (2013)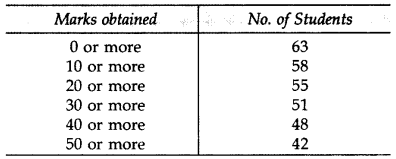

Solution: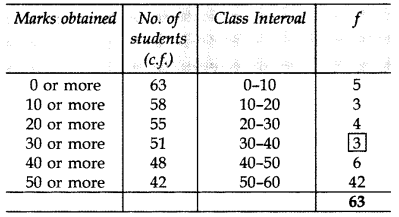

∴ Frequency of class 30 – 40 = 3

Question 4.
Following table shows sale of shoes in a store during one month: (2014)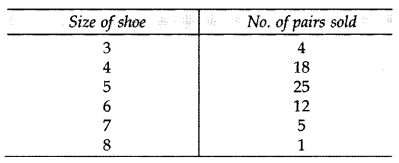

Find the model size of the shoes sold.
Solution:
Maximum no. of pairs sold = 25 (size 5)
∴ Modal size of shoes = 5

Question 5.
Weekly household expenditure of families living in a housing society are shown below: (2014)

Find the upper limit of the modal class.
Solution:
Maximum frequency = 48
∴ Modal class = 9,000 – 12,000
Upper limit of the modal class = 12,000

Statistics Class 10 Important Questions Short Answer-I (2 Marks)

Question 6.
The mean of the following data is 18.75. Find the value of P: (2012, 2017D)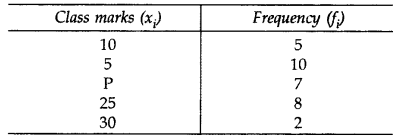

Solution:

Question 7.
Data regarding heights of students of Class X of Model School, Dehradun is given below. Calculate the average height of students of the class. (2015)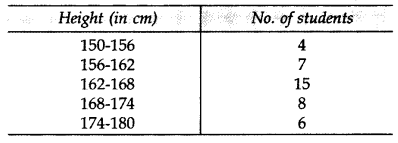

Solution: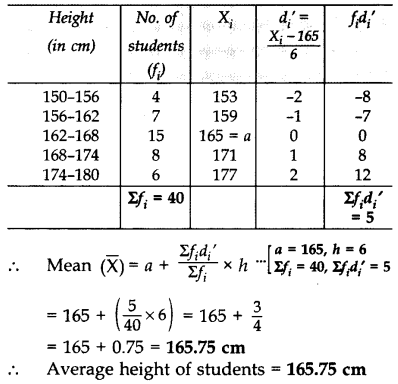

Question 8.
From the following cumulative frequency table, construct a frequency distribution table: (2013)

Solution: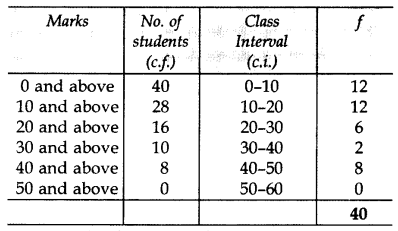

Question 9.
Convert the following frequency distribution to a ‘more than’ type cumulative frequency distribution. (2012)

Solution: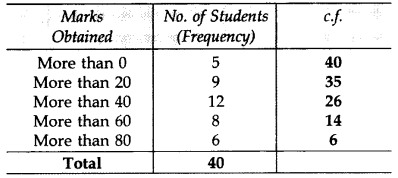

Question 10.
The distribution given below gives the daily income of 50 workers in a factory: (2017D)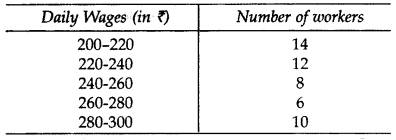

Convert the above distribution to a less than type cumulative frequency distribution.
Solution: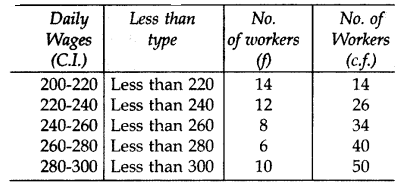

Question 11.
Find the mode of the following frequency distribution: (2013)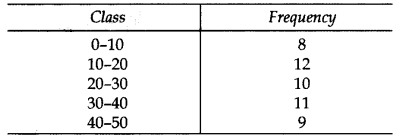

Solution:

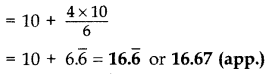
Question 12.
Given below is the distribution of weekly pocket money received by students of a class. Calculate the pocket money that is received by most of the students. (2014)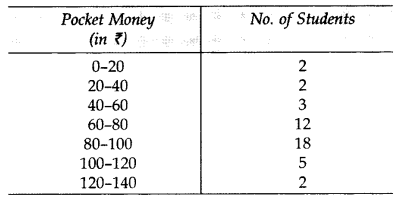

Solution:

∴ Required pocket money = ₹86.32 (approx.)

Question 13.
Find the median of the data using an empirical formula, when it is given that mode = 35.3 and mean = 30.5. (2014)
Solution:
Mode = 3(Median) – 2(Mean)
35.3 = 3(Median) – 2(30.5)
35.3 = 3(Median) – 61
96.3 = 3 Median
Median = \(\frac{96.3}{3}\) = 32.1

Question 14.
Show that the mode of the series obtained by combining the two series S1 and S2 given below is different from that of S1 and S2 taken separately: (2015)
S1 : 3, 5, 8, 8, 9, 12, 13, 9, 9
S2 : 7, 4, 7, 8, 7, 8, 13
Solution:
In S1 : Number 9 occurs 3 times (maximum)
∴ Mode of S1 Series = 9
In S2 : Number 7 occurs 3 times (maximum)
∴ Mode of S, Series = 7
After combination:
In S1 & S2 : No. 8 occurs 4 times (maximum)
∴ Mode of S1 & S2 taken combined = 8
So, mode of S1 & S2 combined is different from that of S1 & S2 taken separately.

Statistics Class 10 Important Questions Short Answer-II (3 Marks)

Question 15.
Find the mean of the following data. (2012)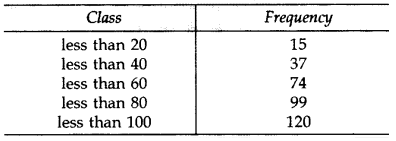

Solution: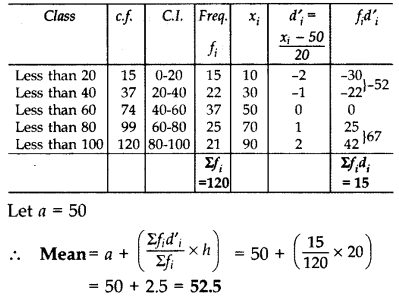

Question 16.
The following table gives the literacy rate (in %) in 40 cities. Find the mean literacy rate: (2012)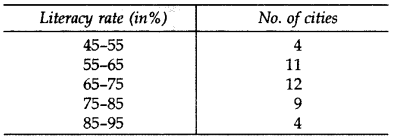

Solution: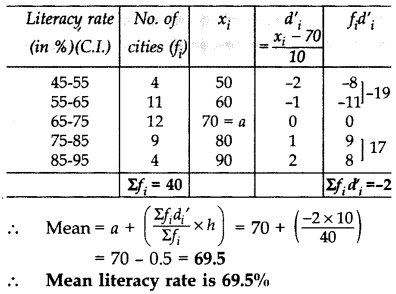

Question 17.
If the mean of the following distribution is 50, find the value of p: (2013)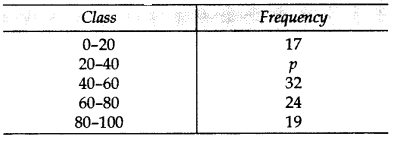

Solution: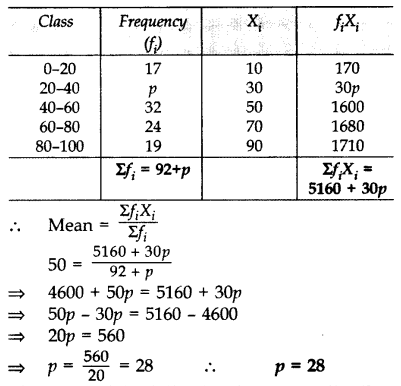

Question 18.
The mean of the following frequency distribution is 62.8. Find the missing frequency x. (2013)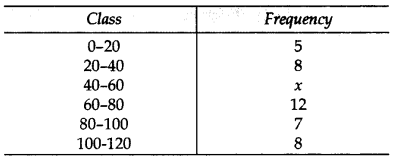

Solution: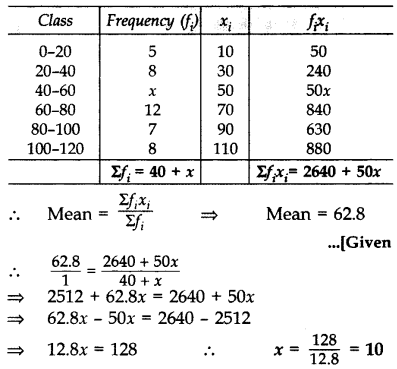

Question 19.
The frequency distribution table of agricultural holdings in a village is given below: (2013)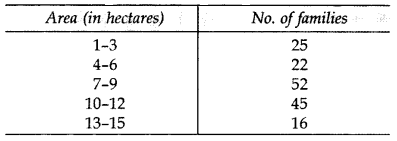

Find the Mean area held by a family.
Solution: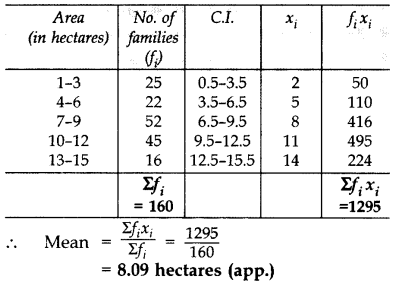

Question 20.
Monthly pocket money of students of a class is given in the following frequency distribution: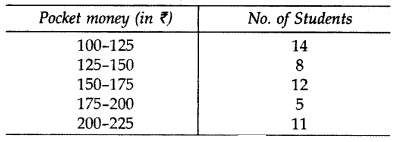

Find mean pocket money using step deviation method. (2014)
Solution: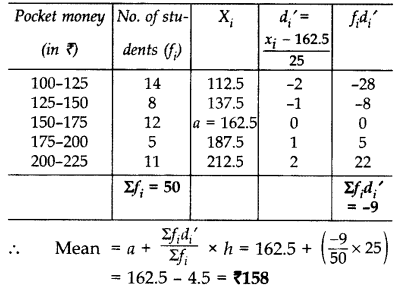

Question 21.
Find the mean of the following distribution by Assumed Mean Method: (2015)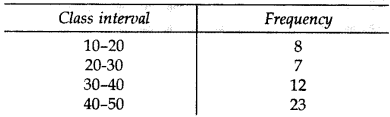


Solution:

Question 22.
Find the mean and median for the following data: (2015)

Solution:

Question 23.
For helping poor girls of their class, students saved pocket money as shown in the following table: (2014)

Find mean and median for this data.
Solution:

Question 24.
Weekly income of 600 families is given below: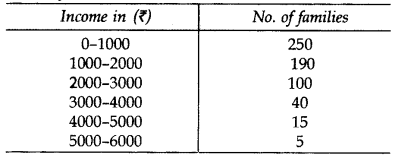

Find the median. (2012)
Solution: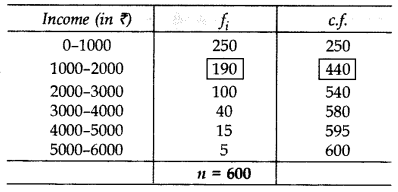

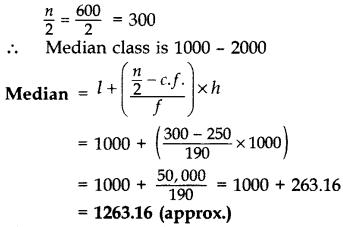
Question 25.
Find the median for the following distribution: (2013)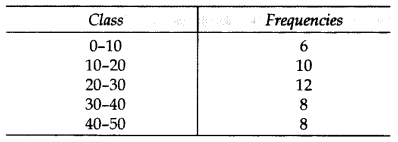

Solution:

Question 26.
Heights of students of class X are given in the following frequency distribution: (2014)

Find the modal height.
Solution:

Maximum frequency is 20
∴ Modal class is 160 – 165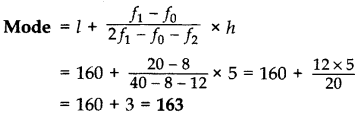

∴ The modal height = 163 cm

Question 27.
A medical camp was held in a school to impart health education and the importance of excercise to children. During this camp, a medical check of 35 students was done and their weights were recorded as follows: (2016)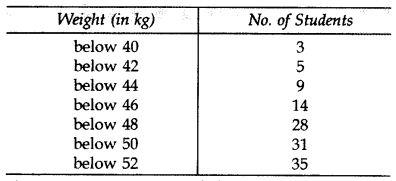

Compute the modal weight.
Solution:

∴ Modal weight = 46.9 kg

Question 28.
The average score of boys in the examination of a school is 71 and that of the girls is 73. The average score of the school in the examination is 71.8. Find the ratio of number of boys to the number of girls who appeared in the examination. (2015)
Solution:
Let the number of boys = n1
and number of girls = n2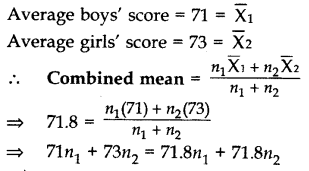


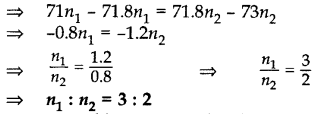
∴ No. of boys : No. of girls = 3 : 2

Question 29.
Following is the age distribution of dengue patients admitted in a hospital during a week of October, 2013: (2014)

Draw a ‘less than type’ ogive for the above distribution. Also, obtain median from the curve.
Solution: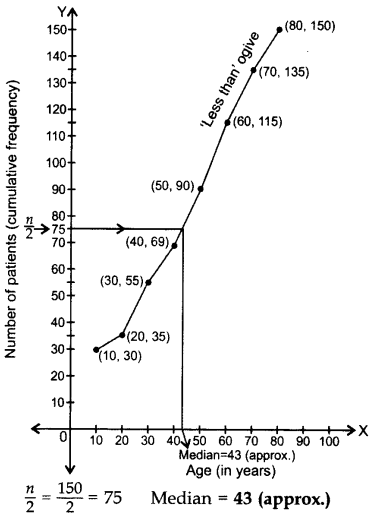

Question 30.
The lengths of leaves of a plant are measured correct to the nearest mm and the data obtained is represented as the following frequency distribution: (2015)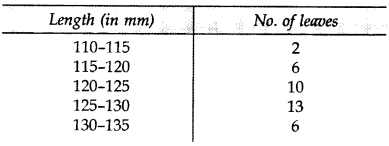


Draw a ‘more than type’ ogive for the above data.
Solution: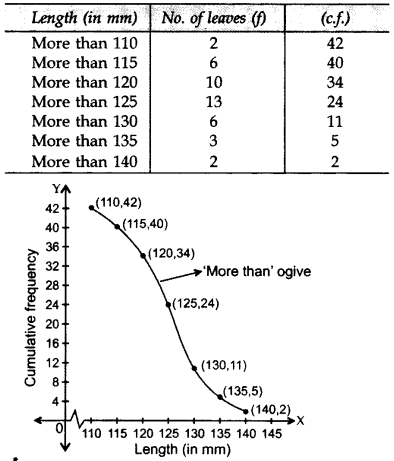

Statistics Class 10 Important Questions Long Answer (4 Marks)

Question 31.
The mean of the following frequency distribu tion is 53. But the frequencies f1 and f2 in the classes 20-40 and 60-80 are missing. Find the missing frequencies: (2013)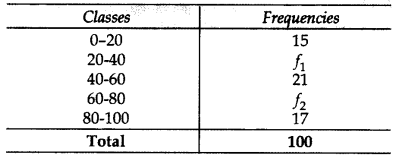

Solution:

⇒ 2730 + 30f1 + 70f2 = 5300
⇒ 30f1 + 70f2 = 5300 – 2730 = 2570
⇒ 3f1 + 7f2 = 257 …[Dividing by 10
⇒ 3f1 +7(47 – f1) = 257 . [From (i)
⇒ 3f1 + 329 – 7f1 = 257
⇒ -4f1 = 257 – 329 = -72
⇒ f1 = \(\frac{-72}{-4}\) = 18
Putting the value of f1 in (i), we get
f2 = 47 – f1
⇒ f2 = 47 – 18 = 29
∴ f1 = 18, f2 = 29

Question 32.
The mean of the following frequency distribution is 62.8 and the sum of frequencies is 50. Find the missing frequencies f1 and f2: (2013)

Solution:

⇒ 2060 + 30f1 + 70f2 = 3140
⇒ 30f1 + 70f2 = 3140 – 2060 = 1080
⇒ 3f1 + 7f2 = 108 …[Dividing by 10
⇒ 3f1 + 7(20 – f1) = 108 … [From (i)
⇒ 3f1 + 140 – 7f1 = 108
⇒ -4f1 = 108 – 140 = -32 .
∴ f1 = 8
Putting the value of f1 into (i), we get
f2 = 20 – 8 = 12
∴ f2 = 12

Question 33.
In the table below, heart-beats of 30 women are recorded. If mean of the data is 76, find the missing frequencies x and y. (2014)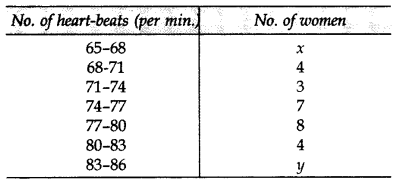

Solution: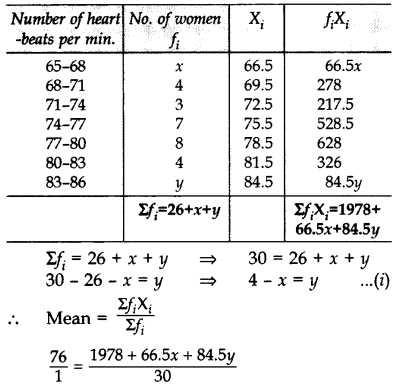

⇒ 1978 + 66.5x + 84.5y = 2280
⇒ 1978 + 66.5x + 84.5(4 – x) = 2280 … [From (i)
⇒ 1978 + 66.5x + 338 – 84.5x = 2280
⇒ 1978 + 338 – 2280 = 84.5x – 66.5x
⇒ 36 = 18x ⇒ x = 2
From (i), y = 4 – x = 4 – 2 = 2 ∴ x = 2, y = 2

Question 34.
The following table gives the daily income of 50 workers of a factory. Draw both types (“less than type” and “greater than type”) ogives. (2015)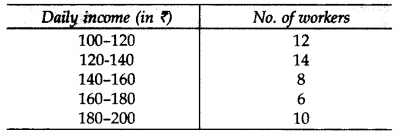

Solution: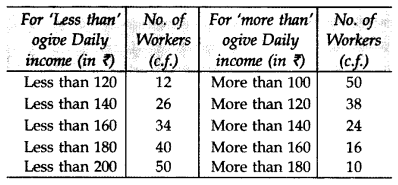

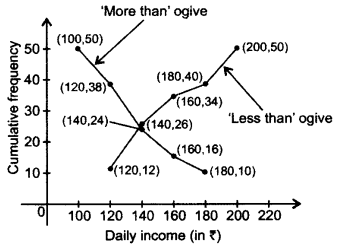
Question 35.
Find the values of x and y if the median for the following data is 31. (2012)

Solution:

⇒ 18 – x = (9 – x)10
⇒ 18 – x = 90 – 10x
⇒ -x + 10x = 90 – 18
⇒ 9x = 72
⇒ x = 8
Putting the value of x in (i), we have
y = 18 – 8 = 10
∴ x = 8, y = 10

Question 36.
The median of the following data is 525. Find x and y if the sum of all frequencies is 100: (2012, 2017 D)

Solution:

Question 37.
Find the missing frequencies f1 and f2 in the following frequency distribution table, if N = 100 and median is 32. (2013)

Solution:

Question 38.
Find the median of the following data: (2013)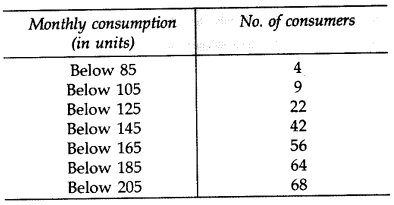

Solution: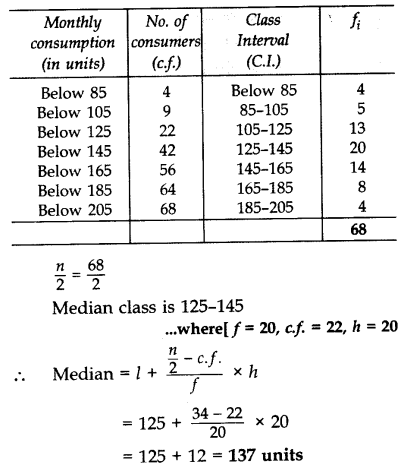

Question 39.
The frequency distribution of weekly pocket money received by a group of students is given below: (2014)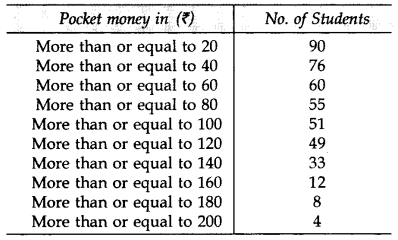

Draw a ‘more than type’ ogive and from it, find median. Verify median by actual calculations.
Solution:
n = 90 …[Given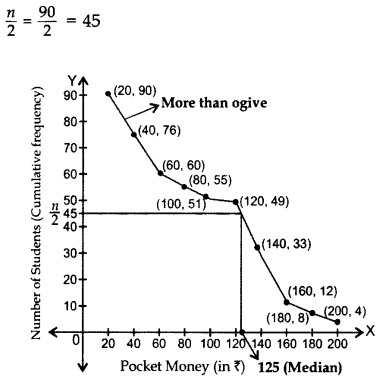

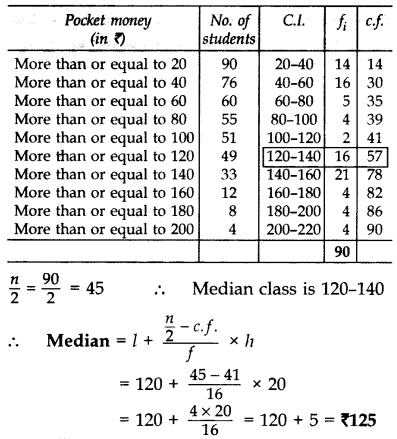
Question 40.
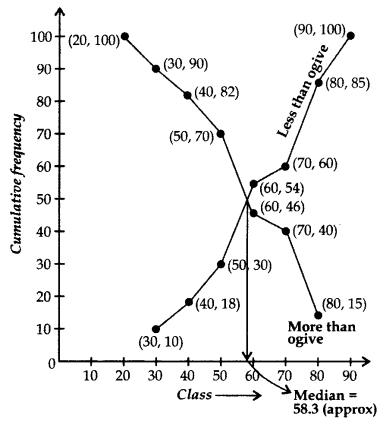
Draw “less than ogive” and “more than ogive” for the following distribution and hence find its median. (2012)

Solution: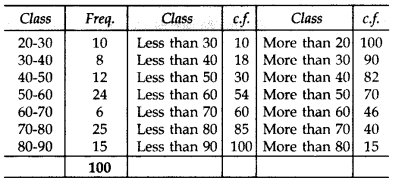

Question 41.
Draw: (a) more than ogive and (2017OD)
(b) less than ogive for the following data
Also find its median.

Solution: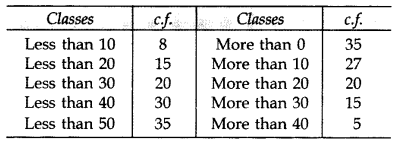

Question 42.
Draw a more than ogive for the data given below which gives the marks of 100 students: (2012, 2017D)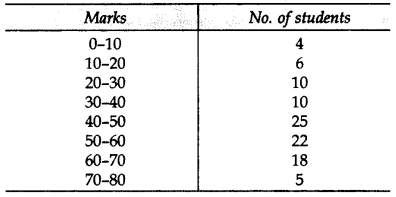

Solution: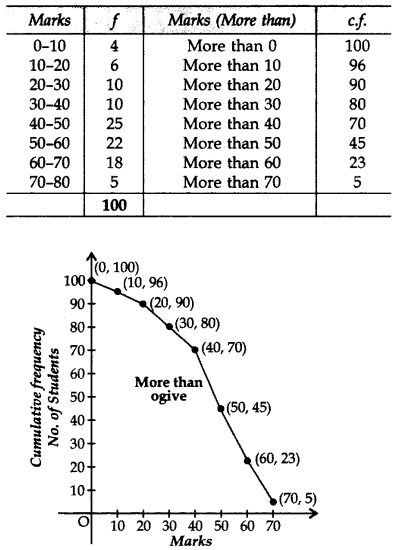

Question 43.
For the following distribution, draw a ‘more than Ogive’ and hence find the median: (2013)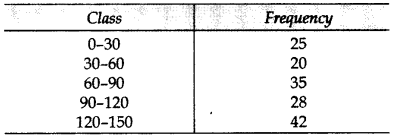

Solution: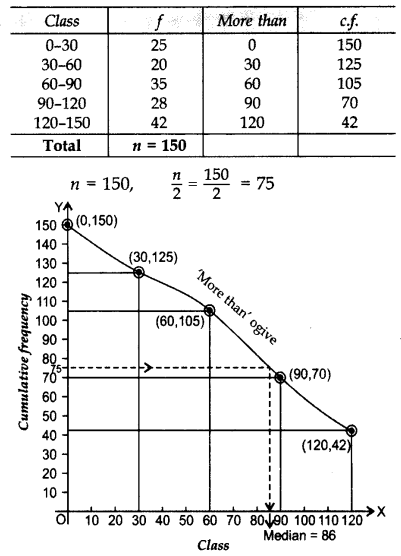

Question 44.
School held sports day in which 150 students participated. Ages of students are given in the following frequency distribution: (2014)

For the above data, draw a ‘more than type’ ogive and from the curve, find median. Verify it by actual calculations.
Solution: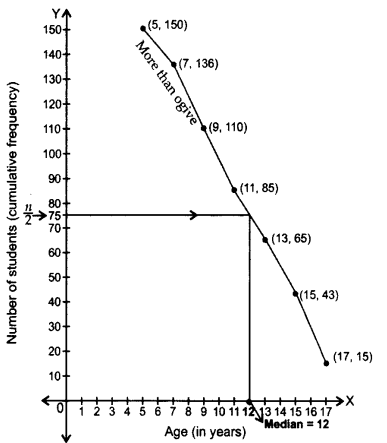

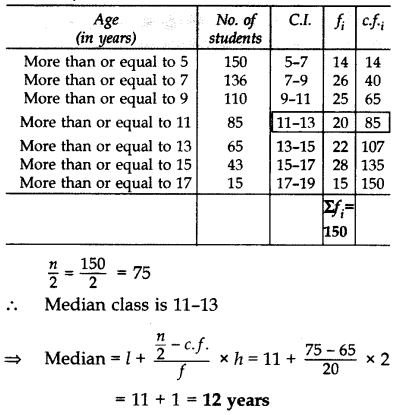
Question 45.
In a class test, marks obtained by 120 students are given in the following frequency distribution. If it is given that mean is 59, find the missing frequencies x and y. (2015)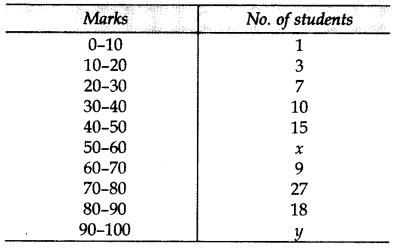

Solution: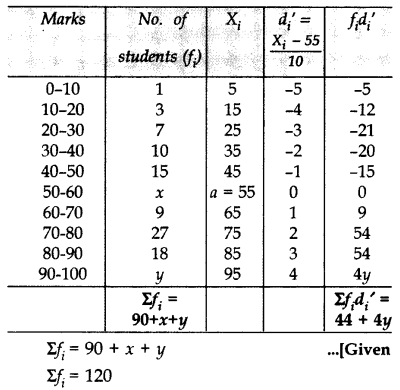

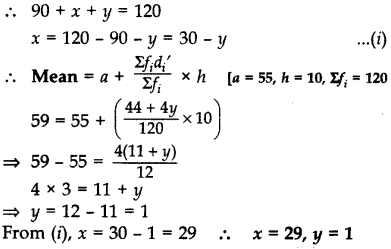
Question 46.
Mode of the following frequency distribution is 65 and sum of all the frequencies is 70. Find the missing frequencies x and y. (2015)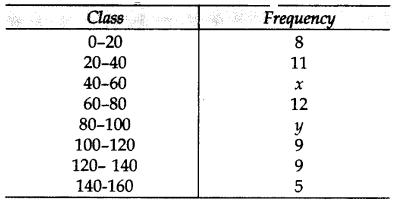

Solution: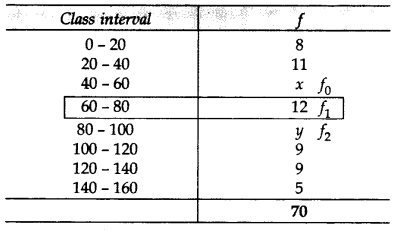

54 + x + y = 70 … [Given
x + y = 70 – 54 = 16 …(i)
∴ Mode = 65
Modal Class is 60 – 80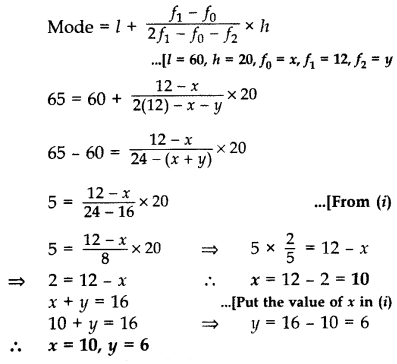

Question 47.
Find the mode of the following frequency distribution: (2015)

Solution:

Question 48.
Cost of Living Index for some period is given in the following frequency distribution: (2014)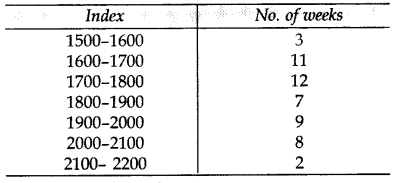

Find the mode and median for above data.
Solution: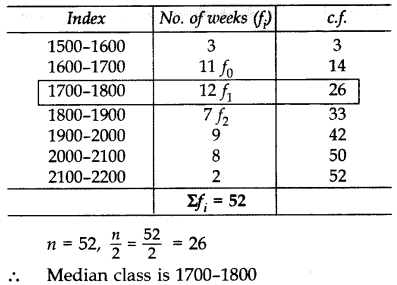

Class 10 Maths Notes Chapter 14 Statistics

MEAN (AVERAGE): Mean [Ungrouped Data] – Mean of n observations, x1, x2, x3 … xn, is

MEAN [Grouped Data]: The mean for grouped data can be found by the following three methods:
(i) Direct Mean Method:

Class Mark = UpperClassLimit+LowerClassLimit

Note: Frequency of a class is centred at its mid-point called class mark.

(ii) Assumed Mean Method: In this, an arbitrary mean ‘a’ is chosen which is called, ‘assumed mean’, somewhere in the middle of all the values of x.

…[where di = (xi – a)]

(iii) Step Deviation Method:

….. [where ui=dih , where h is a common divisor of di]

MEDIAN: Median is a measure of central tendency that gives the value of the middle-most observation in the data.

…where[l = Lower limit of median class; n = Number of observations; f = Frequency of median class; c.f. = Cumulative frequency of preceding class; h = Class size]

(iii) Representing a cumulative frequency distribution graphically as a cumulative frequency curve, or an ogive of the less than type and of the more than type. The median of grouped data can be obtained graphically as the x-coordinate of the point of intersection of the two ogives for this data.

Mode:
(i) Ungrouped Data: The value of the observation having maximum frequency is the mode.
(ii) Grouped Data:

…where[l = Lower limit of modal class; f1 = Frequency of modal class; f0 = Frequency of the class preceding the modal class; f2 = Frequency of the class succeeding the modal class; h = Size of class interval. c.f. = Cumulative frequency of preceding class; h = Class size]

Mode = 3 Median – 2 Mean
Median = Mode+2Mean3
Mean = 3Median−Mode2