Class 7 Maths Chapter 5 Lines and Angles NCERT Solutions

Class 7 Maths Chapter 5 Lines and Angles NCERT Solutions

• Class 7 Maths Lines and Angles Exercise 5.1
• Class 7 Maths Lines and Angles Exercise 5.2

NCERT Solutions for Class 7 Maths Chapter 5 Lines and Angles Exercise 5.1
Ex 5.1 Class 7 Maths Question 1.
Find the complement of each of the following angles: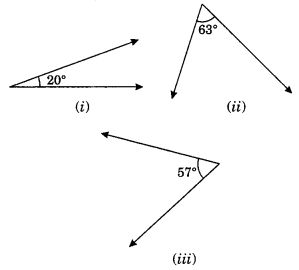

Solution:
(i) Complement of 20° = 90° – 20° = 70°
(ii) Complement of 63° = 90° – 63° = 27°
(iii) Complement of 57° = 90° – 57° = 33°

Ex 5.1 Class 7 Maths Question 2.
Find the supplement of each of the following angles: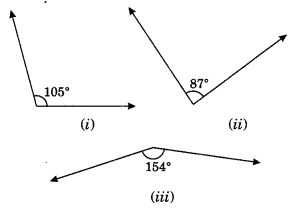

Solution:
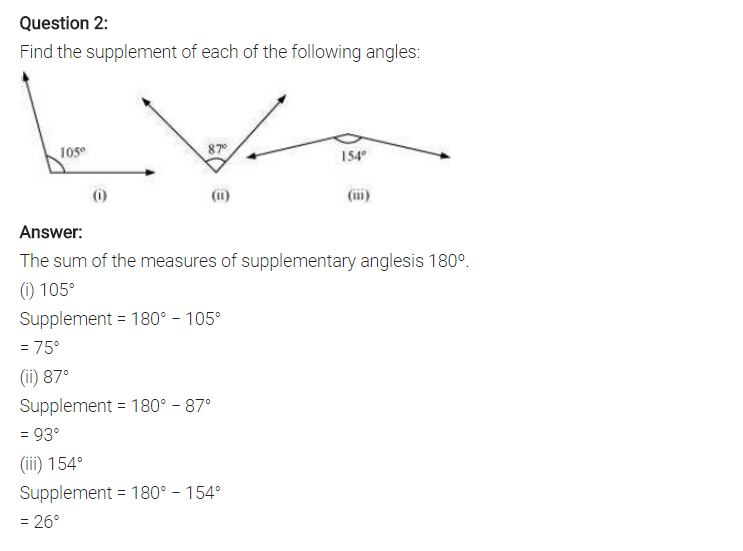
(i) Supplement of 105° = 180° – 105° = 75°
(ii) Supplement of 87° = 180° – 87° = 93°
(iii) Supplement of 154° = 180° – 154° = 26°

Ex 5.1 Class 7 Maths Question 3.
Identify which of the following pairs of angles are complementary and which are supplementary?
(i) 65°, 115°
(ii) 63°, 27°
(iii) 112°, 68°
(iv) 130°, 50°
(v) 45°, 45°
(vi) 80°, 10°
Solution:
(i) 65° (+) 115° = 180°
They are supplementary angles.
(ii) 63° (+) 27° = 90°
They are complementary angles.
(iii) 112° (+) 68° = 180°
They are supplementary angles.
(iv) 130° (+) 50° = 180°
They are supplementary angles.
(v) 45° (+) 45° = 90°
They are complementary angles.
(vi) 80° (+) 10° = 90°
They are complementary angles.

Ex 5.1 Class 7 Maths Question 4.
Find the angle which equal to its complement.
Solution:
Let the required angle be x°.
its complement = (90 – x)°
Now, re = 90 – x ⇒ x + x = 90
⇒ 2x = 90 ∴ x = \(\frac{90}{2}\) = 45°
Thus the required angles are 45°.

Ex 5.1 Class 7 Maths Question 5.
Find the angle which is equal to its supplement.
Solution:
Let the required angle be x°.
∴ it supplement = (180 – x)°
Now, x = 180 – x
⇒ x + x = 180
⇒ 2x = 180°
∴ \(x=\frac{180^{\circ}}{2}=90^{\circ}\)
Thus, the required angle is 90°.

Ex 5.1 Class 7 Maths Question 6.
In the given figure, ∠1 and ∠2 are supplementary angles.
If ∠1 is decreased, what changes should take place in∠2 so that both the angles still remain supplementary.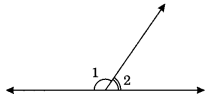

Solution:
∠1 + ∠2 = 180° (given)
If ∠1 is decreased by some degrees, then ∠2 will also be increased by the same degree so that the two angles still remain supplementary.

Ex 5.1 Class 7 Maths Question 7.
Can two angles be supplementary if both of them are:
(i) acute?
(ii) obtuse?
(iii) right?
(ii) Since, acute angle < 90°
∴ Acute angle + acute angle < 90° + 90° < 180° Thus, the two acute angles cannot be supplementary angles. (ii) Since, obtuse angle > 90°
∴ Obtuse angle + obtuse angle > 90° + 90° > 180°
Thus, the two obtuse angles cannot be supplementary angles.
(iii) Since, right angle = 90°
∴ right angle + right angle = 90° + 90° = 180°
Thus, two right angles are supplementary angles.

Ex 5.1 Class 7 Maths Question 8.
An angle is greater than 45°. Is its complementary angle greater than 45° or equal to 45° or less than 45 °?
Solution:
Given angle is greater than 45°
Let the given angle be x°.
∴ x > 45
Complement of x° = 90° – x° < 45° [ ∵ x > 45°]
Thus the required angle is less than 45°.

Ex 5.1 Class 7 Maths Question 9.
In the following figure:
(i) Is ∠1 adjacent to ∠2?
(ii) Is ∠AOC adjacent to∠AOE?
(iii) Do ∠COE and ∠EOD form a linear pair?
(iv) Are ∠BOD and ∠DOA supplementary?
(v) Is ∠1 vertically opposite angle to ∠4?
(vi) What is the vertically opposite angle of ∠5?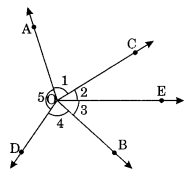

Solution:
(i) Yes, ∠1 and ∠2 are adjacent angles.
(ii) No, ∠AOC is not adjacent to ∠AOE. [ ∵  OC and OE do not lie on either side of common arm OA] .
(iii) Yes, ∠COE and ∠EOD form a linear pair of angles.
(iv) Yes, ∠BOD and ∠DOA are supplementary. [∵ ∠BOD + ∠DOA = 180°]
(v) Yes, ∠1 is vertically opposite to ∠4.
(vi) Vertically opposite angle of ∠5 is ∠2 + ∠3 i.e. ∠BOC.

Ex 5.1 Class 7 Maths Question 10.
Indicate which pairs of angles are:
(i) Vertically opposite angles
(ii) Linear pairs
Solution:
(i) Vertically opposite angles are ∠1 and ∠4, ∠5 and (∠2 + ∠3)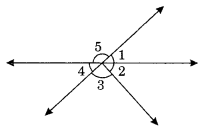

(ii) Linear pairs are
∠1 and ∠5, ∠5 and ∠4

Ex 5.1 Class 7 Maths Question 11.
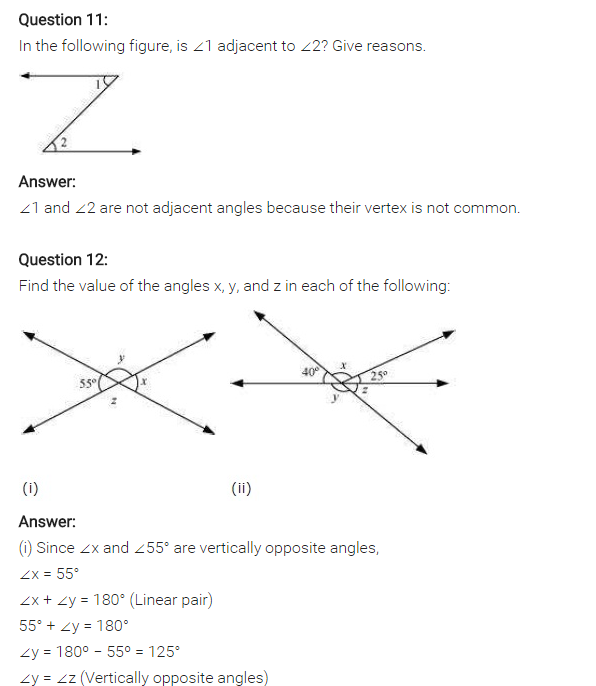
In the following figure, is ∠1 adjacent to ∠2? Give reasons.
Solution:
No, ∠1 and∠2 are not adjacent angles.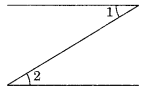

Reasons:
(i) ∠1 + ∠2 ≠ 180°
(ii) They have no common vertex.

Ex 5.1 Class 7 Maths Question 12.
Find the values of the angles x, y and z in each of the following: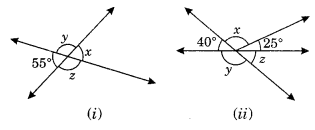

Solution:
From Fig. 1. we have
∠x = ∠55° (Vertically opposite angles)
∠x + ∠y = 180° (Adjacent angles)
55° + ∠y = 180° (Linear pair angles)
∴ ∠y = 180° – 55° = 125°
∠y = ∠z (Vertically opposite angles)
125° = ∠z
Hence, ∠x = 55°, ∠y = 125° and ∠z = 125°

(ii) 25° + x + 40° = 180° (Sum of adjacent angles on straight line)
65° + x = 180°
∴ x = 180° – 65° = 115°
40° + y = 180° (Linear pairs)
∴ y = 180° – 40° = 140°
y + z = 180° (Linear pairs)
140° + z = 180°
∴ z = 180° – 140° = 40°
Hence, x – 115°, y = 140° and z – 40°

Ex 5.1 Class 7 Maths Question 13.
Fill in the blanks:
(i) If two angles are complementary, then the sum of their measures is ______ .
(ii) If two angles are supplementary, then the sum of their measures is ______ .
(iii) Two angles forming a linear pair are ______ .
(iv) If two adjacent angles are supplementary, they form a ______ .
(v) If two lines intersect at a point, then the vertically opposite angles are always ______ .
(vi) If two lines intersect at a point, and if one pair of vertically opposite angles are acute angles, then the other pair of vertically opposite angles are ______ .
Solution:
(i) 90°
(ii) 180°
(iii) Supplementary
(iv) Linear pair
(v) Equal
(vi) Obtuse angle

Ex 5.1 Class 7 Maths Question 14.
In the given figure, name the following pairs of angles.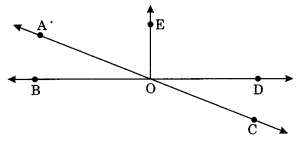

(i) Obtuse vertically opposite angles.
(ii) Adjacent complementary angles.
(iii) Equal supplementary angles.
(iv) Unequal supplementary angles.
(v) Adjacent angles but do not form a linear pair.
Solution:
(i) ∠BOC and ∠AOD are obtuse vertically opposite angles.
(ii) ∠AOB and ∠AOE are adjacent complementary angles.
(iii) ∠EOB and ∠EOD are equal supplementary angles.
(iv) ∠EOA and ∠EOC are unequal supplementary angles.
(v) ∠AOB and ∠AOE, ∠AOE and ∠EOD, ∠EOD and ∠COD are adjacent angles but do not form a linear pair.

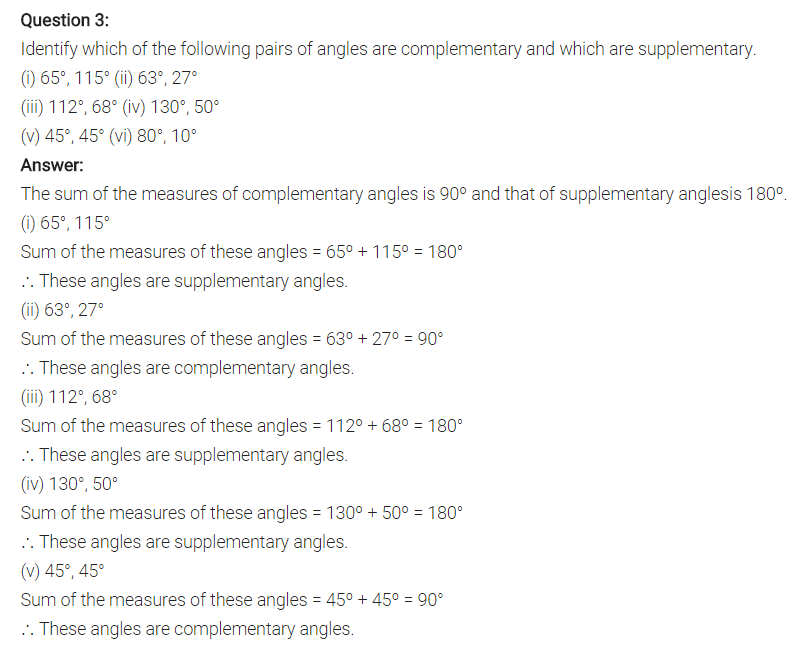
NCERT Solutions for Class 7 Maths Chapter 5 Lines and Angles Exercise 5.2
Ex 5.2 Class 7 Maths Question 1.
State the property that is used in each of the following statements?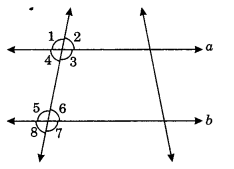

(i) If a || b, then ∠1 = ∠5
(ii) If ∠4 = ∠6, then a || b
(iii) If ∠4 + ∠5 = 180°, then a || b
Solution:
(i) Given a || b
∴ ∠1 = ∠5 (Pair of corresponding angles)
(ii) Given: ∠4 = ∠6
∴ a || b [If pair of alternate angles are equal, then the lines are parallel]
(iii) Given: ∠4 + ∠5 = 180°
∴ a || b [If sum of interior angles is 180°, then the lines are parallel]

Ex 5.2 Class 7 Maths Question 2.
In the given figure, identify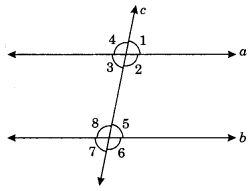

(i) the pairs of corresponding angles.
(ii) the pairs of alternate interior angles.
(iii) the pairs of interior angles on the same side of the transversal.
Solution:
(i) The pair of corresponding angles are ∠1 and ∠5, ∠2 and ∠6, ∠4 and ∠8, ∠3 and ∠7.
(ii) The pairs of alternate interior angles are ∠2 and ∠8, ∠3 and ∠5.
(iii) The pairs of interior angles on the same side of the transversal are ∠2 and ∠5, ∠3 and ∠8.

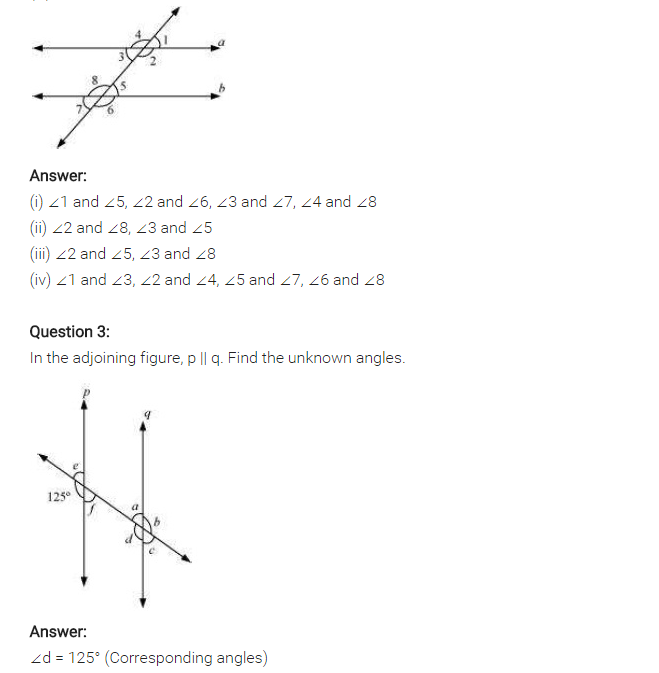
Ex 5.2 Class 7 Maths Question 3.
In the given figure, p || q. Find the unknown angles.
Solution:
∠e + 125° = 180° (Linear pair)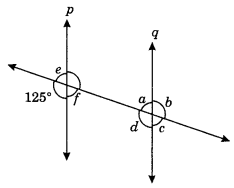

∴ ∠e = 180° – 125° = 55°
∠e = ∠f (Vertically opposite angles)
∴ ∠f= 55°
∠a = ∠f= 55° (Alternate interior angles)
∠c = ∠a = 55° (Vertically opposite angles)
∠d = 125° (Corresponding angles)
∠b = ∠d = 125° (Vertically opposite angles)
Thus, ∠a = 55°, ∠b = 125°, ∠c = 55°, ∠d = 125°, ∠e = 55°, ∠f= 55°.

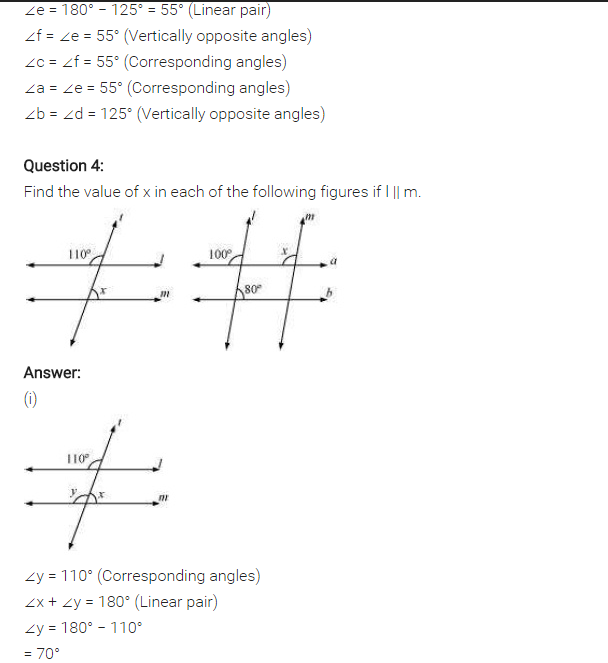
Ex 5.2 Class 7 Maths Question 4.
Find the value of x in each of the following figures if l || m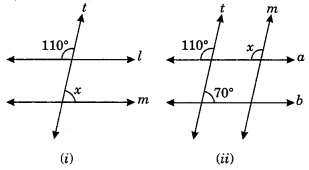

Solution:
(i) Let the angle opposite to 110° be y.
∴ y = 110° (Vertically opposite angles)
∠x + ∠y = 180° (Sum of interior angle on the same side of transversal)
∠x + 110° = 180° .
∴ ∠x = 180° – 110° = 70°
Thus x= 70°
(ii) ∠x = 110° (Pair of corresponding angles)

Ex 5.2 Class 7 Maths Question 5.
In the given figure, the arms of two angles are parallel. If ∠ABC = 70°, then find
(i) ∠DGC
(ii) ∠DEF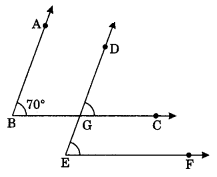

Solution:
Given
AB || DE
BC || EF
∠ABC = 70°
∠DGC = ∠ABC
(i) ∠DGC = 70° (Pair of corresponding angles)
∠DEF = ∠DGC
(ii) ∠DEF = 70° (Pair of corresponding angles)

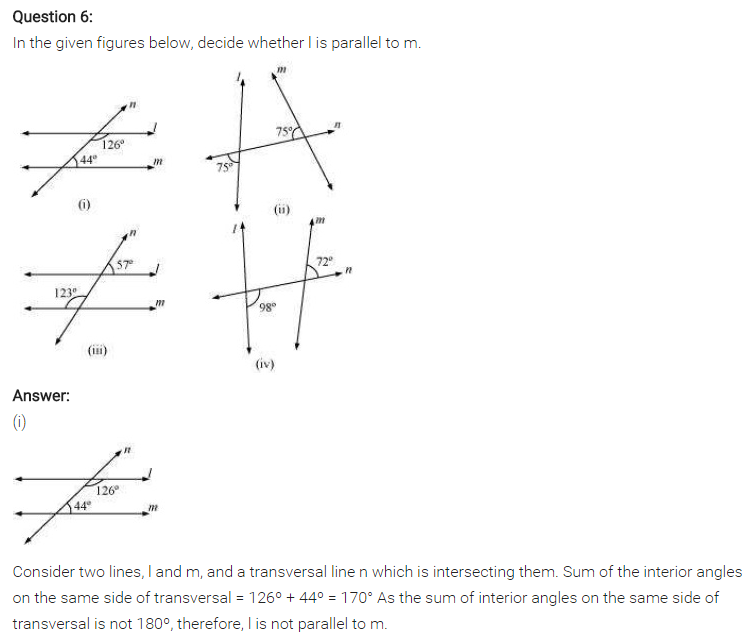
Ex 5.2 Class 7 Maths Question 6.
In the given figure below, decide whether l is parallel to m.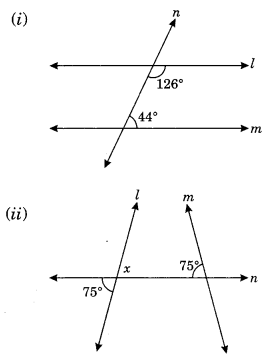

Solution:
Sum of interior angles on the same side of transversal
= 126° + 44° = 170° ≠ 180°
∴ l is not parallel to m.

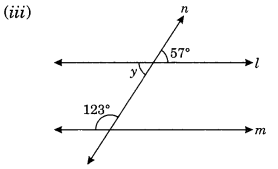
(ii) Let angle opposite to 75° be x.
x = 75° [Vertically opposite angles]
∴ Sum of interior angles on the same side of transversal
= x + 75° = 75° + 75°
= 150° ≠ 180°
∴ l is not parallel to m.

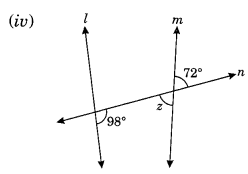
(iii) Let the angle opposite to 57° be y.
∴ ∠y = 57° (Vertically opposite angles)
∴ Sum of interior angles on the same side of transversal
= 57° + 123° = 180°
∴ l is parallel to m.

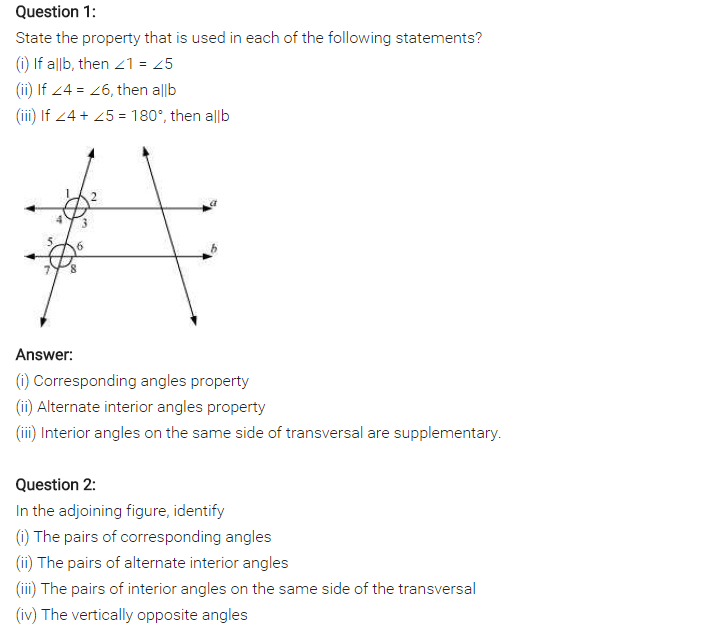
(iv) Let angle opposite to 72° be z.
∴ z = 70° (Vertically opposite angle)
Sum of interior angles on the same side of transversal
= z + 98° = 72° + 98°
= 170° ≠ 180°
∴ l is not parallel to m.

Lines and Angles Class 7 Extra Questions Very Short Answer Type

Question 1.
Find the angles which is 15 of its complement.
Solution:
Let the required angle be x°
its complement = (90 – x)°
As per condition, we get

Question 2.
Find the angles which is 23 of its supplement.
Solution:
Let the required angle be x°.
its supplement = (180 – x)°
As per the condition, we get
23 of (180 – x)° = x°

Question 3.
Find the value of x in the given figure.

Solution:
∠POR + ∠QOR = 180° (Angles of linear pair)
⇒ (2x + 60°) + (3x – 40)° = 180°
⇒ 2x + 60 + 3x – 40 = 180°
⇒ 5x + 20 = 180°
⇒ 5x = 180 – 20 = 160
⇒ x = 32
Thus, the value of x = 32.

Question 4.
In the given figure, find the value of y.

Solution:
Let the angle opposite to 90° be z.
z = 90° (Vertically opposite angle)
3y + z + 30° = 180° (Sum of adjacent angles on a straight line)
⇒ 3y + 90° + 30° = 180°
⇒ 3y + 120° = 180°
⇒ 3y = 180° – 120° = 60°
⇒ y = 20°
Thus the value of y = 20°.

Question 5.
Find the supplements of each of the following:
(i) 30°
(ii) 79°
(iii) 179°
(iv) x°
(v) 25 of right angle
Solution:
(i) Supplement of 30° = 180° – 30° = 150°
(ii) Supplement of 79° = 180° – 79° = 101°
(iii) Supplement of 179° = 180° – 179° = 1°
(iv) Supplement of x° = (180 – x)°
(v) Supplement of 25 of right angle
= 180° – 25 × 90° = 180° – 36° = 144°

Question 6.
If the angles (4x + 4)° and (6x – 4)° are the supplementary angles, find the value of x.
Solution:
(4x + 4)° + (6x – 4)° = 180° (∵ Sum of the supplementary angle is 180°)
⇒ 4x + 4 + 6x – 4 = 180°
⇒ 10x = 180°
⇒ x = 18°
Thus, x = 18°

Question 7.
Find the value of x.

Solution:
(6x – 40)° + (5x + 9)° + (3x + 15) ° = 180° (∵ Sum of adjacent angles on straight line)
⇒ 6x – 40 + 5x + 9 + 3x + 15 = 180°
⇒ 14x – 16 = 180°
⇒ 14x = 180 + 16 = 196
⇒ x = 14
Thus, x = 14

Question 8.
Find the value of y.

Solution:
l || m, and t is a transversal.
y + 135° = 180° (Sum of interior angles on the same side of transversal is 180°)
⇒ y = 180° – 135° = 45°
Thus, y = 45°

Lines and Angles Class 7 Extra Questions Short Answer Type

Question 9.
Find the value ofy in the following figures:

Solution:
(i) y + 15° = 360° (Sum of complete angles round at a point)
⇒ y = 360° – 15° = 345°
Thus, y = 345°
(ii) (2y + 10)° + 50° + 40° + 130° = 360° (Sum of angles round at a point)
⇒ 2y + 10 + 220 = 360
⇒ 2y + 230 = 360
⇒ 2y = 360 – 230
⇒ 2y = 130
⇒ y = 65
Thus, y = 65°
(iii) y + 90° = 180° (Angles of linear pair)
⇒ y = 180° – 90° = 90°
[40° + 140° = 180°, which shows that l is a straight line]

Question 10.
In the following figures, find the lettered angles.

Solution:
(i) Let a be represented by ∠1 and ∠2
∠a = ∠1 + ∠2
∠1 = 35° (Alternate interior angles)
∠2 = 55° (Alternate interior angles)
∠1 + ∠2 = 35° + 55°
∠a = 90°
Thus, ∠a = 90°

Question 11.
In the given figure, prove that AB || CD.

Solution:
∠CEF = 30° + 50° = 80°
∠DCE = 80° (Given)
∠CEF = ∠DCE
But these are alternate interior angle.
CD || EF ……(i)
Now ∠EAB = 130° (Given)
∠AEF = 50° (Given)
∠EAB + ∠AEF = 130° + 50° = 180°
But these are co-interior angles.
AB || EF …(ii)
From eq. (i) and (ii), we get
AB || CD || EF
Hence, AB || CD
Co-interior angles/Allied angles: Sum of interior angles on the same side of transversal is 180°.

Question 12.
In the given figure l || m. Find the values of a, b and c.

Solution:
(i) We have l || m
∠b = 40° (Alternate interior angles)
∠c = 120° (Alternate interior angles)
∠a + ∠b + ∠c = 180° (Sum of adjacent angles on straight angle)
⇒ ∠a + 40° + 120° = 180°
⇒ ∠a + 160° = 180°
⇒ ∠a = 180° – 160° = 20°
Thus, ∠a = 20°, ∠b = 40° and ∠c = 120°.
(ii) We have l || m
∠a = 45° (Alternate interior angles)
∠c = 55° (Alternate interior angles)
∠a + ∠b + ∠c = 180° (Sum of adjacent angles on straight line)
⇒ 45 + ∠b + 55 = 180°
⇒ ∠b + 100 = 180°
⇒ ∠b = 180° – 100°
⇒ ∠b = 80°

Question 13.
In the adjoining figure if x : y : z = 2 : 3 : 4, then find the value of z.

Solution:
Let x = 2s°
y = 3s°
and z = 4s°
∠x + ∠y + ∠z = 180° (Sum of adjacent angles on straight line)
2s° + 3s° + 4s° = 180°
⇒ 9s° = 180°
⇒ s° = 20°
Thus x = 2 × 20° = 40°, y = 3 × 20° = 60° and z = 4 × 20° = 80°

Question 14.
In the following figure, find the value of ∠BOC, if points A, O and B are collinear. (NCERT Exemplar)

Solution:
We have A, O and B are collinear.
∠AOD + ∠DOC + ∠COB = 180° (Sum of adjacent angles on straight line)
(x – 10)° + (4x – 25)° + (x + 5)° = 180°
⇒ x – 10 + 4x – 25 + x + 5 = 180°
⇒ 6x – 10 – 25 + 5 = 180°
⇒ 6x – 30 = 180°
⇒ 6x = 180 + 30 = 210
⇒ x = 35
So, ∠BOC = (x + 5)° = (35 + 5)° = 40°

Question 15.
In given figure, PQ, RS and UT are parallel lines.
(i) If c = 57° and a = c3, find the value of d.
(ii) If c = 75° and a = 25c , find b.

Solution:
(i) We have ∠c = 57° and ∠a = ∠c3
∠a = 573 = 19°
PQ || UT (given)
∠a + ∠b = ∠c (Alternate interior angles)
19° + ∠b = 57°
∠b = 57° – 19° = 38°
PQ || RS (given)
∠b + ∠d = 180° (Co-interior angles)
38° + ∠d = 180°
∠d = 180° – 38° = 142°
Thus, ∠d = 142°
(ii) We have ∠c = 75° and ∠a = 25 ∠c
∠a = 25 × 75° = 30°
PQ || UT (given)
∠a + ∠b = ∠c
30° + ∠b = 75°
∠b = 75° – 30° = 45°
Thus, ∠b = 45°