Class 7 Maths Chapter 11 Perimeter and Area NCERT Solutions
- Class 7 Maths Perimeter and Area Exercise 11.1
- Class 7 Maths Perimeter and Area Exercise 11.2
- Class 7 Maths Perimeter and Area Exercise 11.3
- Class 7 Maths Perimeter and Area Exercise 11.4
NCERT Solutions for Class 7 Maths Chapter 11 Perimeter and Area Exercise 11.1
Ex 11.1 Class 7 Maths Question 1.
The length and the breadth of a rectangular piece of land are 500 m and 300 m respectively. Find
(i) its area
(ii) the cost of the land, if 1 m2 of the land costs ₹ 10,000
Solution:
Given: l = 500 m, b = 300 m
(i) Area = l × b
= 500 m × 300 m = 150000 m2
(ii) Cost of land = ₹ 10,000 × 150000 = ₹ 15,00,000,000
Ex 11.1 Class 7 Maths Question 2.
Find the area of a square park whose perimeter is 320 m.
Solution:
Given: Perimeter = 320 m
Side of the square = \(\frac{\text { Perimeter }}{4}\)
\(=\frac{320}{4} \mathrm{m}=80 \mathrm{m}\)
Area of the square = Side × Side
= 80 m × 80 m = 6400 m2
Ex 11.1 Class 7 Maths Question 3.
Find the breadth of a rectangular plot of land, if its area is 440 m2 and the length is 22 m. Also, find its perimeter.
Solution:
Given: Area = 440 m2
Length = 22 m
Breadth = \(\frac{\text { Area }}{\text { Length }}=\frac{440 \mathrm{m}^{2}}{22 \mathrm{m}}=20 \mathrm{m}\)
Perimeter = 2[l + b] = 2 [22 m + 20 m]
= 2 × 42 m = 84 m
Ex 11.1 Class 7 Maths Question 4.
The perimeter of a rectangular sheet is 100 cm. If the length is 35 cm, find its breadth. Also find the area.
Solution:
Given: Perimeter = 100 cm
Length = 35 cm
Perimeter = 2(l + b)
100 = 2(35 + b)
\(\frac{100}{2}=35+b\)
⇒ 50 = 35 + b
⇒ b = 50 – 35 = 15 cm
∴ Breadth = 15 cm
Area = l × b = 35 cm × 15 cm
= 525 cm2
Ex 11.1 Class 7 Maths Question 5.
The area of a square park is same as of a rectangular park. If the side of the square park is 60 m and the length of the rectangular park is 90 m, find the breadth of the rectangular park.
Solution:
Given: Side of the square park = 60 m Length of the rectangular park = 90 m Area of the rectangular park = Area of the square park
90 m × 6 = 60 m × 60 m
⇒ \(b=\frac{60 \mathrm{m} \times 60 \mathrm{m}}{90}\)
⇒ b = 40m
Hence, the required breadth = 40 m.
Ex 11.1 Class 7 Maths Question 6.
A wire is in the shape of a rectangle. Its length is 40 cm and breadth is 22 cm. If the same wire is rebent in the shape of a square, what will be the measure of each side. Also find which shape encloses more area?
Solution:
Given: Length = 40 cm, Breadth = 22 cm Perimeter of the rectangle
= Length of the wire
= 2(l + b) = 2(40 cm + 22 cm)
= 2 × 62 cm = 124 cm
Now, the wire is rebent into a square.
Perimeter = 124 cm
⇒ 4 × side = 124
∴ side = \(\frac{124}{4}\) cm = 31 cm
So, the measure of each side = 31 cm
Area of rectangular shape = l × b
= 40 cm x 22 cm
= 880 cm2
Area of square shape = (Side)2
= (31)2 = 961 cm2
Since 961 cm2 > 880 cm2
Hence, the square encloses more area.
Ex 11.1 Class 7 Maths Question 7.
The perimeter of a rectangle is 130 cm. If the breadth of the rectangle is 30 cm, find its length. Also find the area of the rectangle.
Solution:
Given: Perimeter = 130 cm
Breadth = 30 cm
Perimeter = 2 (l + b)
130 cm = 2(l + 30 cm)
⇒ \(\frac{130}{2}\) cm = l + 30 cm
⇒ 65 cm = l + 30 cm
⇒ 65 cm – 30 cm = l
∴ l = 35 cm
Area of the rectangle = l × b = 35 cm × 30 cm
= 1050 cm2
Ex 11.1 Class 7 Maths Question 8.
A door of length 2 m and breadth 1 m is fitted in a wall. The length of the wall is 4.5 m and the breadth is 3.6 m. Find the cost of white washing the wall, if the rate of white washing the wall is ₹ 20 per m2.
Solution:
Given: Length of wall = 4.5 m
Breadth of the wall = 3.6 m
Length of the door = 2 m
Breadth of the door = 1 m
Area of the wall = l × b = 4.5 m × 3.6 m = 16.20 m2
= 16.20 m2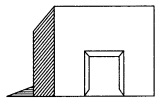
Area of the door = l × b = 2 m × 1 m = 2 m2
∴ Area of the wall to be white washed = Area of the wall – Area of the door
= 16.20 m2 – 2 m2= 14.20 m2
Cost of white washing
= ₹ 14.20 × 20 = ₹ 284.00
Hence, the required area = 14.20 m2 and the required cost = ₹ 284



RD Sharma Class 7 Solutions Mensuration
Exercise 11.2






Exercise 11.3







Exercise 11.4






NCERT Solutions for Class 7 Maths Chapter 11 Perimeter and Area Exercise 11.2
Ex 11.2 Class 7 Maths Question 1.
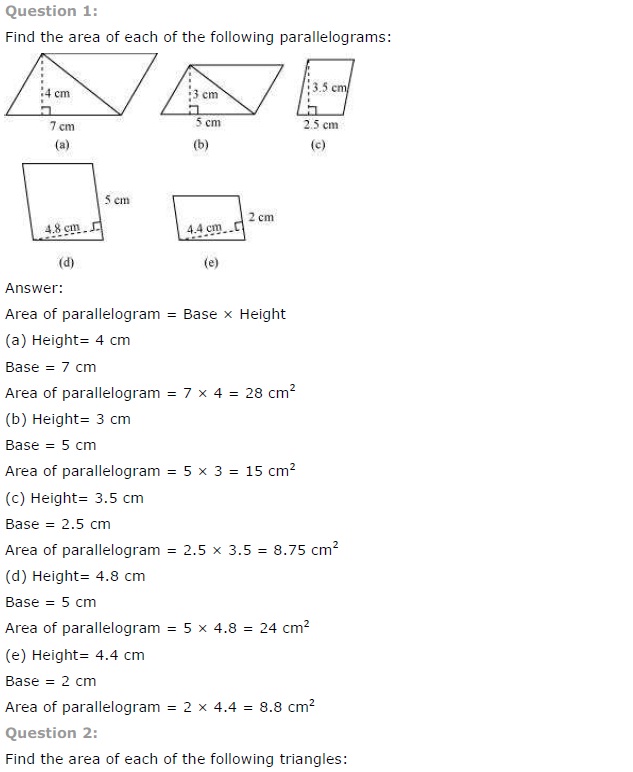
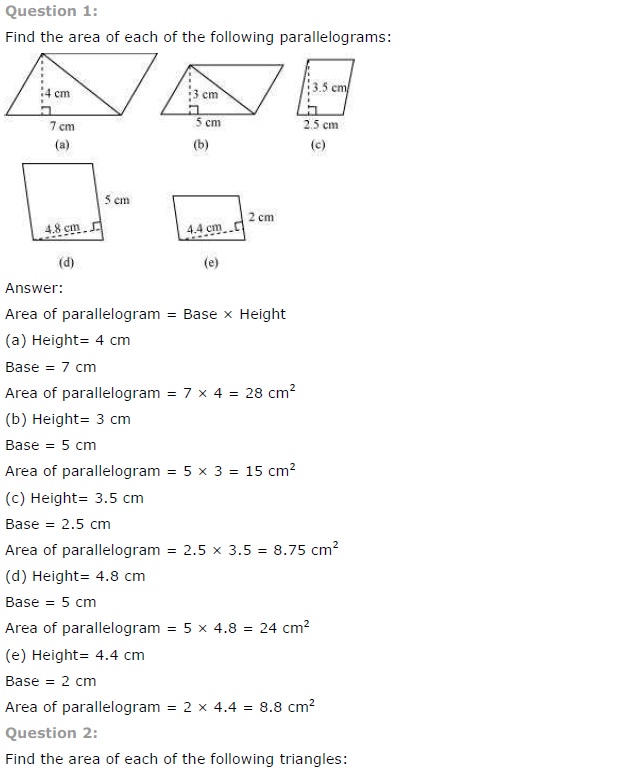
Find the area of each of the following parallelograms: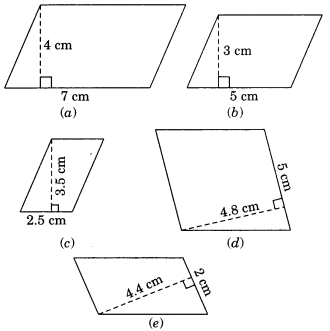
Solution:
(a) Area of the parallelogram
= base × altitude = 7 cm × 4 cm
= 28 cm2
(b) Area of the parallelogram
= base × altitude = 5 cm × 3 cm
= 15 cm2
(c) Area of the parallelogram
= base × altitude = 2.5 cm × 3.5 cm
= 8.75 cm2
(d) Area of the parallelogram
= base × altitude = 5 cm × 4.8 cm
= 24.0 cm2
(e) Area of the parallelogram
= base × altitude = 2 cm × 4.4 cm
= 8.8 cm2
Ex 11.2 Class 7 Maths Question 2.
Find the area of each of the following triangles: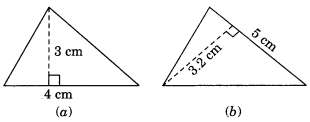
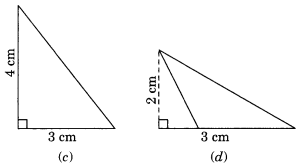
Solution:
Area of the triangle = \(\frac{1}{2}\) × b × h
= \(\frac{1}{2}\) × 4 cm × 3 cm
= 6m2
(b) Area of the triangle = \(\frac{1}{2}\) × b × h
= \(\frac{1}{2}\) × 5 cm × 3.2 cm
= 8.0 cm2
(c) Area of the triangle = \(\frac{1}{2}\) × b × l
= \(\frac{1}{2}\) × 3 cm × 4 cm
= 6 cm2
(d) Area of the triangle = \(\frac{1}{2}\) × b × h
= \(\frac{1}{2}\) × 3 cm × 2 cm
= 3 cm2
Ex 11.2 Class 7 Maths Question 3.
Find the missing values:
| S.No. | Base | Height | Area of the parallelogram |
| (a) | 20 cm | 246 cm2 | |
| (6) | 15 cm | 154.5 cm2 | |
| (c) | 8.4 cm | 48.72 cm2 | |
| (d) | 15.6 | 16.38 cm2 |
Solution:
(a) Area of the parallelogram =b × h
246 = 20 × h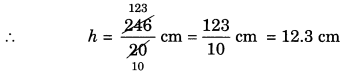
(b) Area of the parallelogram = b × h
154.5 = b × 15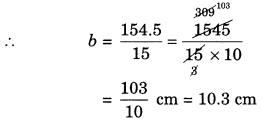
(c) Area of the parallelogram = b × h
48.72 = b × 8.4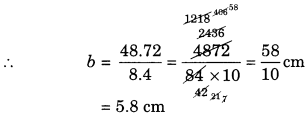
(d) Area of the parallelogram = b × h
16.38 = 15.6 × h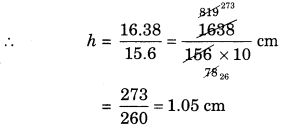
Ex 11.2 Class 7 Maths Question 4.
Find the missing values:
| Base | Height | Area of the triangle |
| 15 cm | — | 87 cm2 |
| — | 31.4 mm | 1256 mm2 |
| 22 cm | — | 170.5 cm2 |
Solution:
(i) Area of the triangle = \(\frac{1}{2}\) × b × h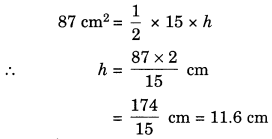
So, the height =11.6 cm
(ii) Area of the triangle = \(\frac{1}{2}\) × b × h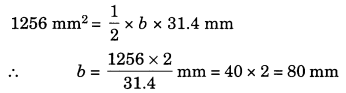
So, the required base = 80 mm.
(iii) Area of the triangle = \(\frac{1}{2}\) × b × h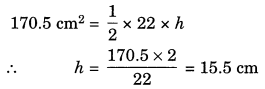
So, the required height = 15.5 cm
Ex 11.2 Class 7 Maths Question 5.
PQRS is a parallelogram. QM is the height of Q to SR and QN is the height from Q to PS. If SR = 12 cm and QM = 7.6 cm. Find:
(a) the area of the parallelogram PQRS
(b) QN, if PS = 8 cm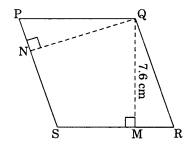
Solution:
(a) Area of the parallelogram PQRS
= SR × QM (∵ Area = Base × Height)
= 12 cm × 7.6 cm
= 91.2 cm2
(b) Area of the parallelogram PQRS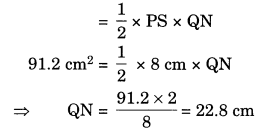
Ex 11.2 Class 7 Maths Question 6.
DL and BM are the heights on sides AB and AD respectively of parallelogram ABCD. If the area of the parallelogram is 1470 cm2, AB = 35 cm and AD = 49 cm, find the length of BM and DL.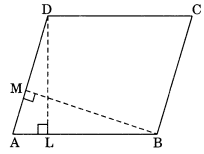
Solution:
Area of the parallelogram ABCD
= AB × DL
⇒ 1470 cm2 = 35 cm × DL
⇒ \(\frac{1470}{35}\) DL
∴ DL = 42 cm
Area of the parallelogram ABCD = AD × BM
1470 cm2 = 49 cm × BM
⇒ \(\frac{1470}{49}\) = 30 cm
∴ BM = 30 cm
Hence, BM = 30 cm and DL = 42 cm
Ex 11.2 Class 7 Maths Question 7.
∆ABC is right angled at A. AD is perpendicular to BC. If AB = 5 cm, BC = 13 cm and AC = 12 cm, find the area of ∆ABC. Also find the length of AD.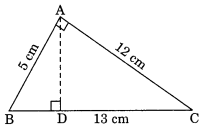
Solution:
Area of right triangle ABC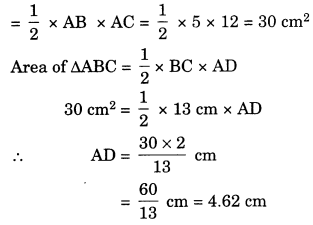
Ex 11.2 Class 7 Maths Question 8.
∆ABC is isosceles with AB = AC = 7.5 cm and BC = 9 cm. The height AD from A to BC, is 6 cm. Find the area of ∆ABC. What will be the height from C to AB i.e., CE?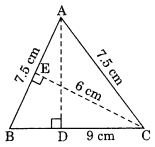
Solution:
Area of ∆ABC = \(\frac{1}{2}\) × base × height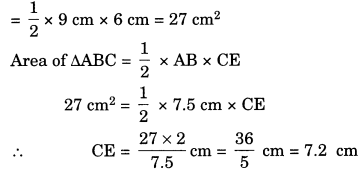






.png)
.png)