Class 7 Maths Chapter 7 Congruence of Triangles NCERT Solutions

Class 7 Maths Chapter 7 Congruence of Triangles NCERT Solutions

• Class 7 Maths Congruence of Triangles Exercise 7.1
• Class 7 Maths Congruence of Triangles Exercise 7.2

NCERT Solutions for Class 7 Maths Chapter 7 Congruence of Triangles Exercise 7.1
Ex 7.1 Class  7 Maths Question 1.
Complete the following statements:
(a) Two line segments are congruent if _______ .
(b) Among the congruent angles, one has a measure of 70°, the measure of the other angle is _______ .
(c) When we write ∠A = ∠B, we actually mean
Solution:
(a) they have the same length
(b) 70°
(c) m∠A = m ∠B

Ex 7.1 Class  7 Maths Question 2.
Give any two real life examples for congruent shapes.
Solution:

• Sharing blades of the same brand.
• Biscuits of the same packets.

Ex 7.1 Class  7 Maths Question 3.
If ∆ABC ≅ ∆FED under the correspondence ABC ⟷ FED, write all the corresponding congruent parts of the triangles.
Solution:
Given: ∆ABC = ∆FED
and ABC ⟷ FED
∴ AB¯¯¯¯¯¯¯↔FE¯¯¯¯¯¯¯,BC¯¯¯¯¯¯¯↔ED¯¯¯¯¯¯¯,AC¯¯¯¯¯¯¯↔FD¯¯¯¯¯¯¯∠A↔∠F,∠B↔∠E,∠C↔∠D

Ex 7.1 Class  7 Maths Question 4.
If ∆DEF ≅ ∆BCA. Write the part of ABCA that correspond to
(i) ∠E
(ii) EF¯¯¯¯¯¯¯
(iii) ∠ZF
(iv) DF¯¯¯¯¯¯¯
Solution:
Given: ∆DEF ≅ ∆BCA
(i) ∠E ⟷ ∠C
(ii) ∠F ⟷ ∠A
(iii) EF ⟷ ZA
(iv) DF ⟷ BA

NCERT Solutions for Class 7 Maths Chapter 7 Congruence of Triangles Exercise 7.2
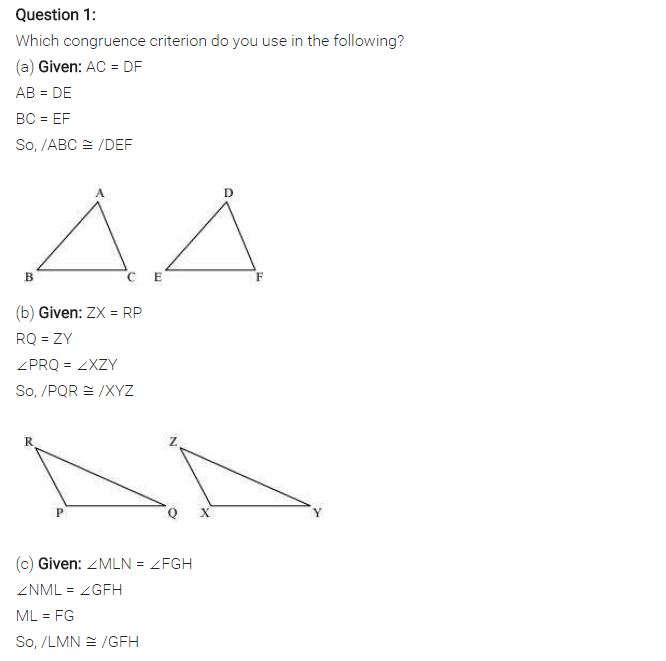
Ex 7.2 Class 7 Maths Question 1.
Which congruence criterion do you use in the following?
(a) Given:
AC = DF
AB = DE
BC = EF
So, ∆ABC = ∆DEF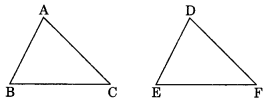

(b) Given:
ZX = RP
RQ = ZY
∠PRQ = ∠XZY
So, ∆PQR ≅ ∆XYZ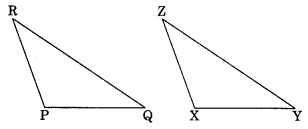

(c) Given: ∠MLN = ∠FGH
∠NML = ∠GFH
ML = FG
So, ∆LMN = ∆GFH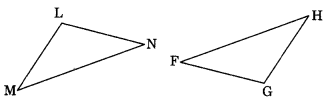

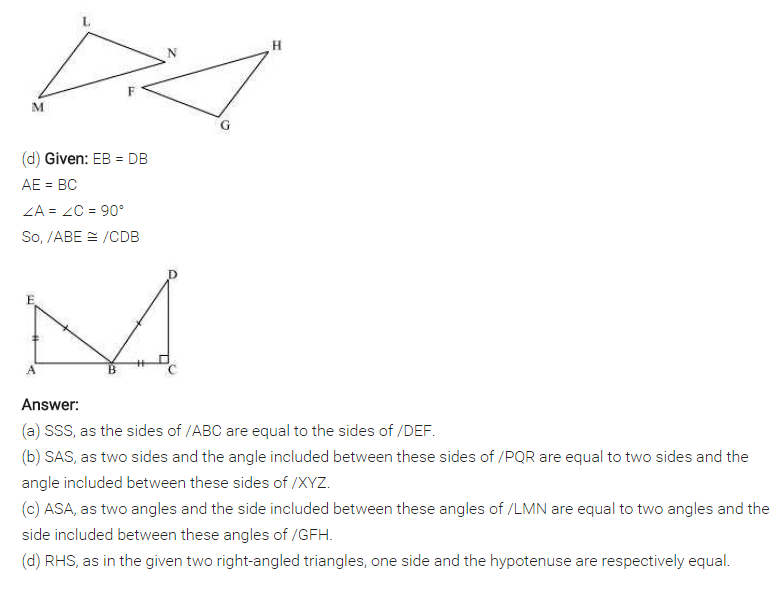
(d) Given:
EB = DB
AE = BC
∠A = ∠C = 90°
∆ABE = ∆CDB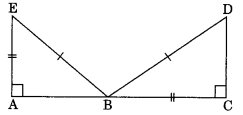

Solution:
(a) ∆ABC ≅ ∆DEF (BY SSS rule)
(b) ∆PQR ≅ ∆XYZ (BY SAS rule)
(c) ∆LMN ≅ ∆GFH (BY ASA rule)
(d) ∆ABE ≅ ∆CDB (BY RHS rule)

Ex 7.2 Class 7 Maths Question 2.
You want to show that ∆ART = ∆PEN,
(a) If you have to use SSS criterion, then you need to show
(i) AR =
(ii) RT =
(iii) AT =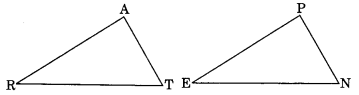

(b) If it is given that ∠T = ∠N and you are to use SAS criterion, you need to have
(i) RT = and
(ii) PN =
(c) If it is given that AT = PN and you are to use ASA criterion, you need to have
(i) ZA
(ii) ZT
Solution:
(a) For SSS criterion, we need
(i) AR = PE
(ii) RT = EN
(iii) AT = PN
(b) For SAS criterion, we need
(i) RT = EN and
(ii) PN = AT
(c) For ASA criterion, we need
(i) ∠A = ∠P
(ii) ∠T = ∠N

Ex 7.2 Class 7 Maths Question 3.
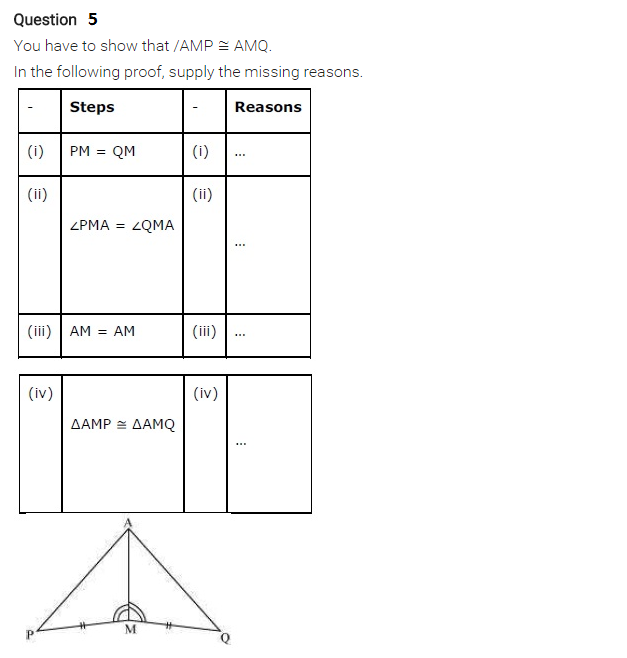
You have to show that ∆AMP ≅ ∆AMQ. In the fallowing proof, supply the missing reasons.

Steps		Reasons
(i) PM = QM		(i)
(ii) ∠PMA – ∠QMA		(ii)
(iii) AM = AM		(iii)
(iv) ∆AMP = ∆AMQ		(iv)

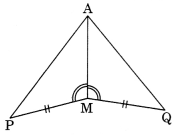
Solution:

Steps		Reasons
(i) PM = QM		(i) Given
(ii) ∠PMA = ∠QMA		(ii) Given
(iii) AM = AM		(iii) Common
(iv) ∆AMP = ∆AMQ		(iv) SAS rule

Ex 7.2 Class 7 Maths Question 4.
In ∆ABC, ∠A = 30°, ∠B = 40° and ∠C = 110°
In ∆PQR, ∠P = 30°, ∠Q = 40° and ∠R = 110°.
A student says that ∆ABC = ∆PQR by AAA congruence criterion. Is he justified? Why or why not?
Solution:
The student is not justified because there is not criterion for AAA congruence rule.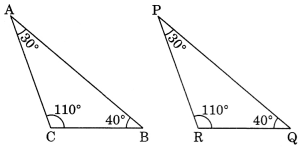

Example: In ∆ABC and ∆PQR, we have ∠A = 30°, ∠B = 40°, ∠C = 110°
∠P = 30°, ∠Q = 40°, ∠R = 110°
But ∆ABC is not congruent to ∆PQR.

Ex 7.2 Class 7 Maths Question 5.
In the figure, the two triangles are congruent. The corresponding parts are marked. We can write ∆RAT ≅ ?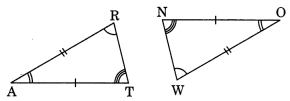

Solution:
In ∆RAT and ∆WON
AT¯¯¯¯¯¯¯=ON¯¯¯¯¯¯¯¯ (Given)
AR¯¯¯¯¯¯¯=OW¯¯¯¯¯¯¯¯¯ (Given)
∠A = ∠O (Given)
∴ ∆RAT ≅ ∆WON (By SAS rule)

Ex 7.2 Class 7 Maths Question 6.
Complete the congruence statement: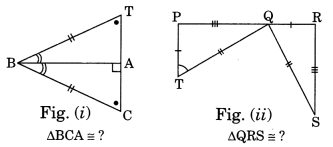

Solution:
Refer to Fig. (i)
In ∆BCA and ∆BTA
∠C = ∠T (Given)
BC¯¯¯¯¯¯¯=BT¯¯¯¯¯¯¯ (Given)
∠BA = ∠TBA (Given)
∴ ∆BCA = ∆BTA (by ADA rule)
Refer to Fig. (ii)
In ∆QRS and ∆TPQ
RS¯¯¯¯¯¯¯=PQ¯¯¯¯¯¯¯ (Given)
QS¯¯¯¯¯¯¯=TQ¯¯¯¯¯¯¯¯ (Given)
∠RSQ = ∠PQT (Given)
∴ ∆QRS = ∆TPQ (by SAS rule)

Ex 7.2 Class 7 Maths Question 7.
In a squared sheet, draw two triangles of equal areas such that:
(i) the triangles are congruent.
(ii) the triangle are not congruent.
What can you say about their perimeters?
Solution:
(i) On the given square sheet, we have draw two congruent triangles i.e.
∆ABC = ∆DEF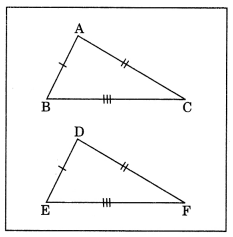

such that
AB¯¯¯¯¯¯¯=DE¯¯¯¯¯¯¯,BC¯¯¯¯¯¯¯=EF¯¯¯¯¯¯¯ and AC¯¯¯¯¯¯¯=DF¯¯¯¯¯¯¯
On adding, we get
AB¯¯¯¯¯¯¯+BC−→+AC−→−=DE¯¯¯¯¯¯¯+EF¯¯¯¯¯¯¯+DF¯¯¯¯¯¯¯
i.e. perimeters of ∆ABC = Perimeter of ∆DEF

(ii) On the other square sheet, we have drawn two triangles ABC and PQR which are not congruent.
Such that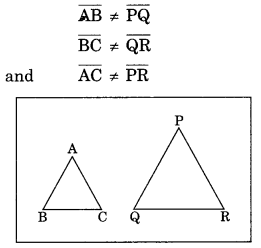

Adding both sides, we get
AB¯¯¯¯¯¯¯+BC¯¯¯¯¯¯¯+AC¯¯¯¯¯¯¯≠PQ¯¯¯¯¯¯¯+QR¯¯¯¯¯¯¯¯+PR¯¯¯¯¯¯¯
i.e., perimeter of ∆ABC ≠ the perimeter of ∆PQR.

Ex 7.2 Class 7 Maths Question 8.
Draw a rough sketch of two triangles, such that they have five pairs of congruent parts but still
the triangles are not congruent.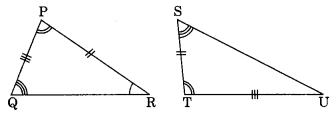

Solution:
We have ∆PQR and ∆TSU
PQ¯¯¯¯¯¯¯=SU¯¯¯¯¯¯¯ (Given)
PR¯¯¯¯¯¯¯=ST¯¯¯¯¯¯ (Given)
∠Q = ∠S (Given)
∠P = ∠T (Given)
∠R = ∠U (Given)
Since non of the criteria of congruence is relevant here.
∴ ∆PQR and ∆TSU are not congruent.

Ex 7.2 Class 7 Maths Question 9.
If ∆ABC and ∆PQR are to be congruent, name one additional pair of corresponding parts. What criterion did you use?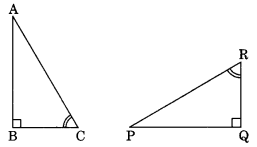

Solution:
In ∆ABC and ∆PQR
∠B = ∠Q (Given)
∠C = ∠R (Given)
For ∆ABC = ∆PQR
BC must equal to QR¯¯¯¯¯¯¯¯ criterion that we used is ASA rule.
Hence, the additional pair of corresponding part is BC¯¯¯¯¯¯¯=QR¯¯¯¯¯¯¯¯.

Ex 7.2 Class 7 Maths Question 10.
Explain, why ∆ABC = ∆FED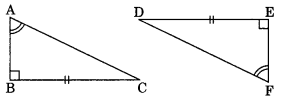

Solution:
In ∆ABC and ∆FED
∠B = ∠E = 90° (Given)
∠A = ∠F (Given)
∴ ∠A + ∠B = ∠E + ∠F
180° – ∠C = 180° – ∠D
[Angle sum property of triangles]
∴ ∠C =∠D
BC = ED (Given)
∴ ∆ABC = ∆FED (By ASA rule)

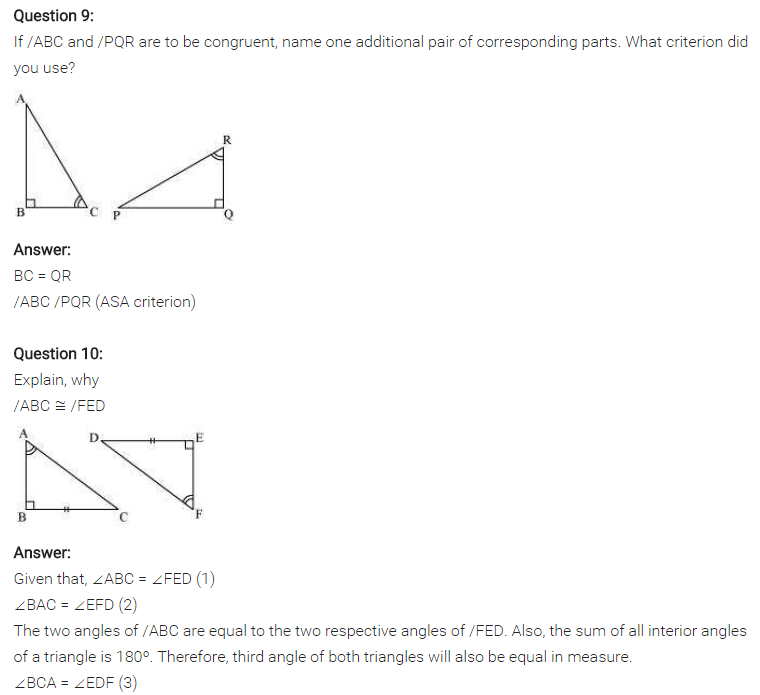
Question 8.
Draw a rough sketch of two triangles such that they have five pairs of congruent parts but still the triangles are not congruent.
Solution:
In some special cases (which depend on the lengths of the sides and the size of the angle involved),

SSA is enough to show congruence. However, it is not always enough. Consider the following triangles :

Here side AB is congruent to side DE (S) side AC is congruent to side DF(S) angle C is congruent to angle F(A)

But the triangles are not congruent, as we can see.

What happens is this : If we draw a vertical line through point A in the first triangle, we can sort of “flip” side AB around this line to get the second triangle. If we were to lay one triangle on top of the other and draw the vertical line, this how it would look.

Clearly, side DE is just side AB flipped around the line. So, we have not changed the length of the side, and the other side AC (or DF) is unchanged, as is angle C (or F). So, these two triangles that have the same SSA information, but they are not congruent.

Congruence of Triangles Class 7 Extra Questions Very Short Answer Type

Question 1.
In the given figure, name
(a) the side opposite to vertex A
(b) the vertex opposite A to side AB
(c) the angle opposite to side AC
(d) the angle made by the sides CB and CA.

Solution:
(a) The side opposite to vertex A is BC.
(b) The vertex opposite to side AB is C.
(c) The angle opposite to side AB is ∠ACB.
(d) The angle made by the sides CB and CA is ∠ACB.

Question 2.
Examine whether the given triangles are congruent or not.
Solution:
Here,
AB = DE = 3 cm
BC = DF = 3.5 cm
AC = EF = 4.5 cm
ΔABC = ΔEDF (By SSS rule)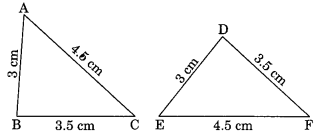

So, ΔABC and ΔEDF are congruent.

Question 3.
In the given congruent triangles under ASA, find the value of x and y, ΔPQR = ΔSTU.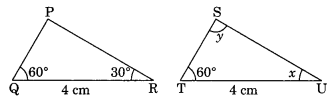

Solution:
Given: ΔPQR = ΔSTU (By ASA rule)
∠Q = ∠T = 60° (given)
QR¯ = TU¯ = 4 cm (given)
∠x = 30° (for ASA rule)
Now in ΔSTU,
∠S + ∠T + ∠U = 180° (Angle sum property)
∠y + 60° + ∠x = 180°
∠y + 60° + 30° = 180°
∠y + 90° = 180°
∠y = 180° – 90° = 90°
Hence, x = 30° and y = 90°.

Question 4.
In the following figure, show that ΔPSQ = ΔPSR.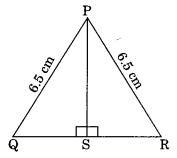

Solution:
In ΔPSQ and ΔPSR
PQ¯ = PR¯ = 6.5 cm (Given)
PS¯ = PS¯ (Common)
∠PSQ = ∠PSR = 90° (Given)
ΔPSQ = ΔPSR (By RHS rule)

Question 5.
Can two equilateral triangles always be congruent? Give reasons.
Solution:
No, any two equilateral triangles are not always congruent.
Reason: Each angle of an equilateral triangle is 60° but their corresponding sides cannot always be the same.

Question 6.
In the given figure, AP = BQ, PR = QS. Show that ΔAPS = ΔBQR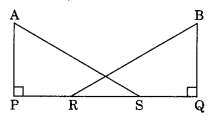

Solution:
In ΔAPS and ΔBQR
AP = BQ (Given)
PR = QS (Given)
PR + RS = QS + RS (Adding RS to both sides)
PS = QR
∠APS = ∠BQR = 90° (Given)
ΔAPS = ΔBQR (by SAS rule)

Question 7.
Without drawing the figures of the triangles, write all six pairs of equal measures in each of the following pairs of congruent triangles.
(i) ΔABC = ADEF
(ii) ΔXYZ = ΔMLN
Solution:
(i) Given: ΔABC = ΔDEF
Here AB = DE
BC = EF
AC = DF
∠A = ∠D, ∠B = ∠E and ∠C = ∠F
(ii) Given ΔXYZ = ΔMLN
Here XY = ML
YZ = LN
XZ = MN
∠X = ∠M, ∠Y = ∠L and ∠Z = ∠N

Question 8.
Lengths of two sides of an isosceles triangle are 5 cm and 8 cm, find the perimeter of the triangle.
Solution:
Since the lengths of any two sides of an isosceles triangle are equal, then
Case I: The three sides of the triangle are 5 cm, 5 cm and 8 cm.
Perimeter of the triangle = 5 cm + 5 cm + 8 cm = 18 cm
Case II: The three sides of the triangle are 5 cm, 8 cm and 8 cm.
Perimeter of the triangle = 5 cm + 8 cm + 8 cm = 21 cm
Hence, the required perimeter is 18 cm or 21 cm.

Question 9.
Write the rule of congruence in the following pairs of congruent triangles.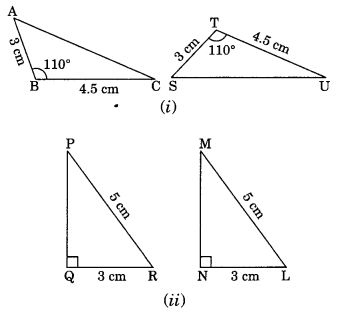

Solution:
(i) Here, AB = ST = 3 cm
BC = TU = 4.5 cm
∠ABC = ∠STU = 110°
ΔABC = ΔSTU (By SAS rule)
(ii) Here ∠PQR = ∠MNL = 90°
hypt. PR = hypt. ML
QR = NL = 3 cm
ΔPQR = ΔMNL (By RHS rule)

Question 10.
In the given figure, state the rule of congruence followed by congruent triangles LMN and ONM.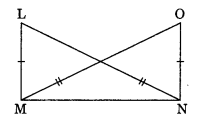

Solution:
In ΔLMN and ΔONM
LM = ON
LN = OM
MN = NM
ΔLMN = ΔONM

Congruence of Triangles Class 7 Extra Questions Short Answer Type

Question 11.
In the given figure, PQR is a triangle in which PQ = PR. QM and RN are the medians of the triangle. Prove that
(i) ΔNQR = ΔMRQ
(ii) QM = RN
(iii) ΔPMQ = ΔPNR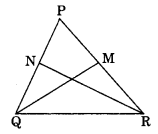

Solution:
ΔPQR is an isosceles triangle. [∵ PQ = PR]
⇒ 12 PQ = 12 PR
⇒ NQ = MR and PN = PM
(i) In ΔNQR and ΔMRQ
NQ = MR (Half of equal sides)
∠NQR = ∠MRQ (Angles opposite to equal sides)
QR = RQ (Common)
ΔNQR = ΔMRQ (By SAS rule)
(ii) QM = RN (Congruent parts of congruent triangles)
(iii) In ΔPMQ and ΔPNR
PN = PM (Half of equal sides)
PR = PQ (Given)
∠P = ∠P (Common)
ΔPMQ = ΔPNR (By SAS rule)

Question 12.
In the given figure, PQ = CB, PA = CR, ∠P = ∠C. Is ΔQPR = ΔBCA? If yes, state the criterion of congruence.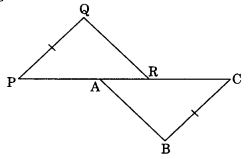

Solution:
Given:
PQ = CB, PA = CR
and ∠P = ∠C
In ΔQPR and ΔBCA,
PQ = CB (Given)
∠QPR = ∠BCA (Given)
PA = CR (Given)
PA + AR = CR + AR (Adding AR to both sides)
or PR = CA
ΔQPR = ΔBCA (By SAS rule)

Question 13.
In the given figure, state whether ΔABC = ΔEOD or not. If yes, state the criterion of congruence.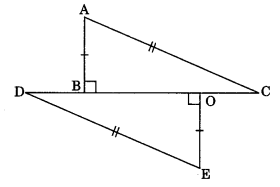

Solution:
In ΔABC and ΔEOD
AB = OE
∠ABC = ∠EOD = 90°
AC = ED
ΔABC = ΔEOD
Hence, ΔABC = ΔEOD
RHS is the criterion of congruence.

Question 14.
In the given figure, PQ || RS and PQ = RS. Prove that ΔPUQ = ΔSUR.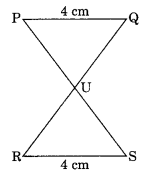

Solution:
In ΔPUQ and ΔSUR
PQ = SR = 4 cm
∠UPQ = ∠USR (Alternate interior angles)
∠PQU = ∠SRU (Alternate interior angles)
ΔPUQ = ΔSUR (By ASA rule)

Congruence of Triangles Class 7 Extra Questions Long Answer Type

Question 15.
In the given figure ΔBAC = ΔQRP by SAS criterion of congruence. Find the value of x and y.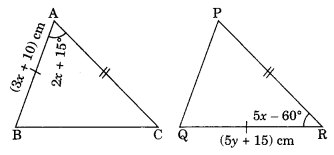

Solution:
Given: ΔBAC = ΔQRP (By SAS rule)
So, BA = QR
⇒ 3x + 10 = 5y + 15 ……(i)
∠BAC = ∠QRP
⇒ 2x + 15° = 5x – 60° ……(ii)
From eq. (ii), we have
2x + 15 = 5x – 60
⇒ 2x – 5x = -15 – 60
⇒ -3x = -7 5
⇒ x = 25
From eq. (i), we have
3x + 10 = 5y + 15
⇒ 3 × 25 + 10 = 5y + 15
⇒ 75 + 10 = 5y + 15
⇒ 85 = 5y + 15
⇒ 85 – 15 = 5y
⇒ 70 = 5y
⇒ y = 14
Hence, the required values of x andy are 25 and 14 respectively.

Question 16.
Observe the figure and state the three pairs of equal parts in triangles ABC and DCB.
(i) Is ΔABC = ΔDCB? Why?
(ii) Is AB = DC? Why?
(iii) Is AC = DB? Why? (NCERT Exemplar)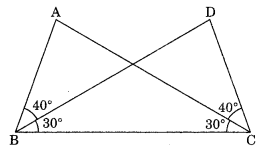

Solution:
(i) In ΔABC and ΔDCB
∠ABC = ∠DCB = 70° (40° + 30° = 70°) (Given)
∠ACB = ∠DCB = 30° (Given)
BC = CB (Common)
ΔABC = ΔDCB (By ASA rule)
(ii) Yes,
AB = DC (Congruent parts of congruent triangles)
(iii) Yes,
AC = DB (Congruent parts of congruent triangles)

Question 17.
In the given figure, ΔQPS = ΔSRQ. Find each value.
(a) x
(b) ∠PQS
(c) ∠PSR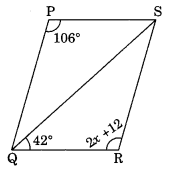

Solution:
(a) ΔQPS = ΔSRQ
∠QPS = ∠SRQ (Congruent part of congruent triangles)
106 = 2x + 12
⇒ 106 – 12 = 2x
⇒ 94 = 2x
⇒ x = 47
∠QRS = 2 × 47 + 12 = 94 + 12 = 106°
So, PQRS is a parallelogram.
∠QSR = 180° – (42° + 106°) = 180° – 148° = 32°
(b) ∠PQS = 32° (alternate interior angles)
(c) ∠PSQ = 180° – (∠QPS + ∠PQS) = 180° – (106° + 32°) = 180° – 138° = 42°
∠PSR = 32° + 42° = 74°

Congruence of Triangles Class 7 Extra Questions Higher Order Thinking Skills (HOTS) Type

Question 18.
In ΔABC, medians BD and CE are equal and intersect each other at O. Prove that ΔABC is an isosceles triangle.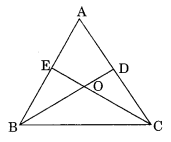

Solution:
We know that the medians of a triangle intersect each other in the ratio 2 : 1.
BD = CE (Given)
23 BD = 23 CE
⇒ OB = OC
13 BD = 13 CE
⇒ OE = OD
In ΔBOE and ΔCOD,
OB = OC
OE = OD
∠BOE = ∠COD (Vertically opposite angles)
ΔBOE = ΔCOD (By SAS rule)
BE = CD (Congruent parts of congruent triangles)
2BE = 2CD
⇒ AB = AC
Hence ΔABC is an isosceles triangle.

Question 19.
Prove that the lengths of altitudes drawn to equal sides of an isosceles triangle are also equal.
(i) ∠TRQ = ∠SQR?
(ii) If ∠TRQ = 30°, find the base angles of the ΔPQR.
(iii) Is ΔPQR an equilateral triangle?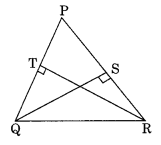

Solution:
In ΔQTR and ΔRSQ
∠QTR = ∠RSQ = 90° (Given)
∠TQR = ∠SRQ (Base angle of an isosceles triangle)
∠QRT = ∠RQS (Remaining third angles)
QR = QR (Common)
ΔQTR = ΔRSQ (By ASA rule)
QS = RT (Congruent parts of congruent triangles)
Hence proved.
(i) ∠TRQ = ∠SQR (Congruent parts of congruent triangles)
(ii) In ΔQTR,
∠TRQ = 30° (Given)
∠QTR + ∠TQR + ∠QRT = 180° (Angle sum property)
⇒ 90° + ∠TQR + 30° = 180°
⇒ 120° + ∠TQR = 180°
⇒ ∠TQR = 180° – 120° = 60°
⇒ ∠TQR = ∠SRQ = 60°
Each base angle = 60°
(iii) In ΔPQR,
∠P + ∠Q + ∠R = 180° (Angle sum property)
⇒ ∠P + 60° + 60° = 180° (From ii)
⇒ ∠P + 120° = 180°
⇒ ∠P = 180° – 120° = 60°
Hence, ΔPQR is an equilateral triangle.

Extra Questions for Class 7 Maths