Class 7 Maths Chapter 8 Comparing Quantities NCERT Solutions

Class 7 Maths Chapter 8 Comparing Quantities NCERT Solutions

• Class 7 Maths Comparing Quantities Exercise 8.1 
• Class 7 Maths Comparing Quantities Exercise 8.2
• Class 7 Maths Comparing Quantities Exercise 8.3

NCERT Solutions for Class 7 Maths Chapter 8 Comparing Quantities Exercise 8.1
Ex 8.1 Class 7 Maths Question 1.
Find the ratio of:
(a) ₹ 5 to 50 paise
(b) 15 kg to 210 g
(c) 9 m to 27 cm
(d) 30 days to 36 hours
Solution:
(a) ₹ 5 to 50 paise
Converting the given quantities into same units, we have
₹ 5 = 5 × 100 = 500 paise
∴ ₹ 5 : 50 paise
= 500 paise : 50 paise [∵ ₹ 1 = 100 paise]
= 10 : 1
So, required ratio is 10 : 1.

(b) 15 kg to 210 g
Converting the given quantities into same units, we have
15 kg = 15 × 1000
= 15000 g [∵ 1 kg = 1000 g]
∴ 15 kg : 210 g = 15000 g : 210 g
= 1500 : 21
= 500 : 7
So, the required ratio is 500 : 7.

(c) 9 m to 27 cm
Converting the given quantities into same units, we have
9 m = 9 × 100 = 900 cm
∴ 9m: 27 cm = 900 cm : 27 cm [∵ 1 m = 100 cm]
= 100 : 3
So, the required ratio is 100 : 3.

(d) 30 days to 36 hours
Converting the given quantities into same
units, we have
30 days = 30 × 24 hours [ ∵ 1 day = 24 hours]
= 720 hours
∴ 30 days : 36 hours
= 720 hours : 36 hours = 20:1
So, the required ratio is 20 : 1.

Ex 8.1 Class 7 Maths Question 2.
In a computer lab, there are 3 computers for every 6 students. How many computers will be needed for 24 students?
Solution:
Using Unitary Method, we have
6 students require 3 computers
∴ 1 student will require = 36 computers
∴ 24 students will require = 36 x 24 computers
= 3 × 4 computers = 12 computers
Hence the number of computers required = 12.

Ex 8.1 Class 7 Maths Question 3.
Population of Rajasthan = 570 lakhs and population of UP = 1660 lakhs.
Area of Rajasthan = 3 lakh km2 and area of UP = 2 lakh km2.
(i) How many people are there per km2 in both these States?
(ii) Which State is less populated?
Solution:
Given:
Population of Rajasthan = 570 lakhs
Population of UP = 1660 lakhs
Area of Rajasthan = 3 lakh km2
Area of UP = 2 lakh km2
(i) Number of people per km2 of Rajasthan 5
=570 lakhs 3 lakh km2
= 190 per km2
Number of people in UP = 1660 lakhs
Area of UP = 2 lakh km2
Number of people per km2 of UP
= =1660 lakhs 2 lakh km2=830 per km2
Since 190 per km2< 830 per km2
(ii) Rajasthan is less populated state.

NCERT Solutions for Class 7 Maths Chapter 8 Comparing Quantities Exercise 8.2

Ex 8.2 Class 7 Maths Question 1.
Convert the given fractional numbers to per cents: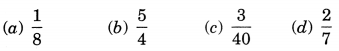

Solution:

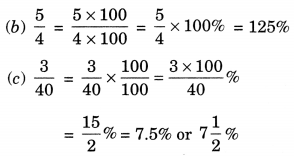
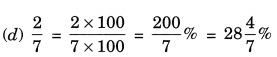
Ex 8.2 Class 7 Maths Question 2.
Convert the given decimal fractions to per cents:
(а) 0.65
(b) 2.1
(c) 0.02
(d) 12.35
Solution:
(a) 0.65 = 0.65×100100 = 0.65 × 100% = 65%
(b) 2.1 = 2.1×100100 = 2.1 ×100% = 210%
(c) 0.02 = 0.02×100100 = 0.02 × 100% = 2%
(d) 12.35 = 12.35×100100 = 12.35 × 100% = 1235%

Ex 8.2 Class 7 Maths Question 3.
Estimate what part of the figures is coloured and hence find the per cent which is coloured.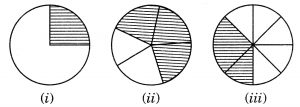

Solution:
(i) Fraction of coloured part = 14
∴ Percentage of coloured parts 100

(ii) Fraction of coloured part = 36
∴ Percentage of coloured parts

(iii) Fraction of coloured part = 68
∴ Percentage of coloured parts

Ex 8.2 Class 7 Maths Question 4.
Find:
(a) 15% of 250
(b) 1% of 1 hour
(c) 20% of ₹ 2500
(d) 75% of 1 kg
Solution:
(a) 15% of 250 = 15100×250=752=37.5
(b) 1% of 1 hour = 1% of 60 minutes [∵ 1 h = 60 min.]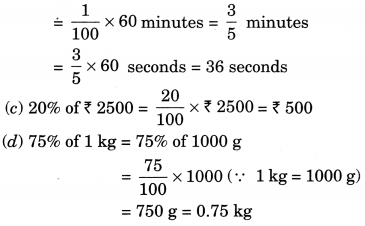

Ex 8.2 Class 7 Maths Question 5.
Find the whole quantity if
(a) 5% of it is 600
(b) 12% of it is? 1080
(c) 40% of it is 500 km
(d) 70% of it is 14 minutes
(e) 8% of it is 40 litres
Solution:
Let the required whole quantity be x.
(a) 5% of x = 600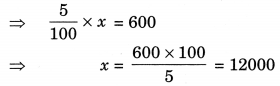

Thus the required whole quantity is 12,000.

(b) 12% of x = ₹ 1080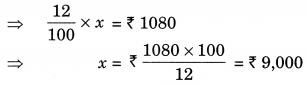

Thus, the required quantity is ₹ 9,000.

(c) 40% of x = 500 km

Thus, the required quantity = 1250 km.

(d) 70% of x = 14 minutes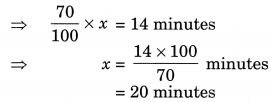

Thus, the required quantity = 20 minutes,

(e) 8% of x = 40 litre 8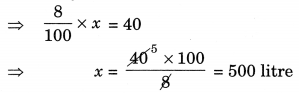

Thus, the required quantity = 500 litres

Ex 8.2 Class 7 Maths Question 6.
Convert given per cents to decimal fractions and also to fractions in simplest forms:
(a) 25%
(b) 150%
(c) 20%
(d) 5%
Solution: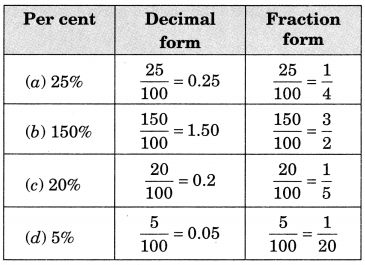

Ex 8.2 Class 7 Maths Question 7.
In a city, 30% are females, 40% are males and remaining are children. What per cent are children?
Solution:
Given: 30% are females
40% are males
Total Percentage of females and males
= 30% + 40% = 70%
∴ Percentage of children
= (100 – 70)% = 30%

Ex 8.2 Class 7 Maths Question 8.
Out of 15,000 voters in a constituency, 60% voted. Find the Percentage of voters who did not vote. Can you now find how many actually did not vote?
Solution:
Total number of voters = 15,000
Percentage of the voters who voted = 60%
∴ Percentage of the voters who did not vote
= (100 – 60)% = 40%
Actual number of voters who did not vote
= 40% of 15,000
=40100×15,000=6,000

Ex 8.2 Class 7 Maths Question 9.
Meena saves ₹ 400 from her salary. If this is 10% of her salary. What is her salary?
Solution:
Let Meena’s salary by ₹ x.
∴ 10% of x = ₹ 400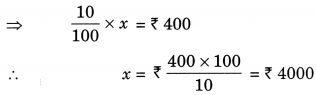

Thus, her salary is ₹ 4000.

Ex 8.2 Class 7 Maths Question 10.
A local cricket team played 20 matches in one season. It won 25% of them. How many matches did they win?
Solution:
Number of matches played by the cricket team = 20
Percentage of the matches won by them = 25%
i.e. 25100×20=5 matches
Thus, the number of matches won by them = 5

NCERT Solutions for Class 7 Maths Chapter 8 Comparing Quantities Exercise 8.3
Ex 8.3 Class 7 Maths Question 1.
Tell what is the profit or loss in the following transactions. Also find profit per cent or loss per cent in each case.
(a) Gardening shears bought for ₹ 250 and sold for ₹ 325.
(b) A refrigerator bought for ₹ 12,000 and sold at ₹ 13,500.
(c) A cupboard bought for ₹ 2,500 and sold at ₹ 3,000.
(d) A skirt bought for ₹ 250 and sold at ₹ 150.
Solution:
(a) Here, CP = ₹ 250
SP = ₹ 325
Since SP > CP
∴ Profit = SP – CP
= ₹ 325 – ₹ 250 = ₹ 75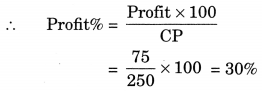

Hence, the required profit = ₹ 75
and Profit per cent = 30%

(b) Here, CP = ₹ 12,000
SP = ₹ 13,500
Since SP > CP
∴ Profit = SP – CP
= ₹ 13,500 – ₹ 12,000 = ₹ 1,500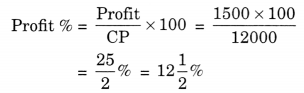

Hence, the required profit = ₹ 1500 × 100
profit % = 1212%

(c) Here, CP = ₹ 2500
SP = ₹ 3000
Since SP > CP
∴ Profit = SP – CP
= ₹ 3000 – ₹ 2500 = ₹ 500

Hence, the required profit = ₹ 500 and profit% = 20%

(d) Here, CP = ₹ 250
SP = ₹ 150
Here CP > SP
∴ Loss = CP – SP
= ₹ 250 – ₹ 150 = ₹ 100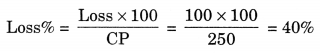

Hence, the required loss = ₹ 100 and loss% = 40%

Ex 8.3 Class 7 Maths Question 2.
Convert each part of the ratio to Percentage:
(a) 3:1
(b) 2:3:5
(c) 1 : 4
(d) 1:2:5
Solution:
(a) 3 : 1
Sum of the ratio parts = 3 + 1 = 4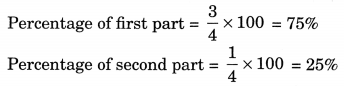

(b) 2 : 3 : 5
Sum of the ratio parts = 2 + 3 + 5 = 10

(c) 1 : 4
Sum of the ratio parts =1 + 4 = 5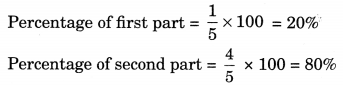

(d) 1 : 2 : 5
Sum of the ratio parts = 1 + 2 + 5 = 8

Ex 8.3 Class 7 Maths Question 3.
The population of a city decreased from 25,000 to 24,500. Find the Percentage decrease.
Solution:
Initial population = 25,000
Decreased population = 24,500
Decrease in population
= 25,000 – 24,500 = 500
Percentage of decrease = 500×10025000 = 2%
Hence the Percentage of decrease in population = 2%.

Ex 8.3 Class 7 Maths Question 4.
Arun bought a car for ₹ 3,50,000. The next year, the price went upto ₹ 3,70,000. What was the Percentage of price increase?
Solution:
Original price of the car = ₹ 3,50,000
Price increased next year = ₹ 3,70,000
Increase in price = ₹ 3,70,000 – ₹ 3,50,000
= ₹ 20,000
∴ Percentage of the increase in the price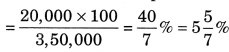

Hence, the Percentage of increase in price = 557%

Ex 8.3 Class 7 Maths Question 5.
I buy a TV for ₹ 10,000 and sell it at a profit of 20%. How much money do I get for it?
Solution:
Here, CP = ₹ 10,000
Profit = 20%
SP = ?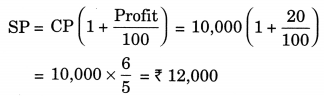

Hence, the required money got by me = ₹ 12,000.

Ex 8.3 Class 7 Maths Question 6.
Juhi sells a washing machine for ₹ 13,500. She loses 20% in the bargain. What was the price at which she bought it?
Solution:
SP of the washing machine = ₹ 13,500
Loss = 20%
CP = ?

Hence, the cost price of the machine = ₹ 16875.

Ex 8.3 Class 7 Maths Question 7.
(i) Chalk contains calcium, carbon and oxygen in the ratio 10 : 3 : 12. Find the Percentage of carbon in chalk.
(ii) If in a stick of chalk, carbon is 3 g, what is the weight of the chalk stick?
Solution:
(i) Sum of the ratio parts = 10 + 3 + 12 = 25
∴ Percentage of carbon in chalk
= =325×100%=12%
Hence, the Percentage of carbon in chalk = 12%

(ii) Weight of carbon = 3 g
∴ Weight of chalk = =33 × 25 g = 25 g
Hence, the weight of chalk = 25 g

Ex 8.3 Class 7 Maths Question 8.
Amina buys a book for ₹ 275 and sells it at a loss of 15%. How much does she sell it for?
Solution:
CP of book = ₹ 275
Loss = 15%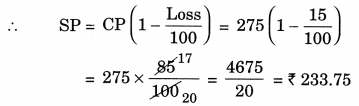

Hence, the required selling price = ₹ 233.75

Ex 8.3 Class 7 Maths Question 9.
Find the amount to be paid at the end of 3 years in each case.
(a) Principal = ₹ 1200 at 12% p.a.
(b) Principal = ₹ 7500 at 5% p.a.
Solution:
(a) Given: Principal = ₹ 1200
Rate of interest = 12% p.a., T = 3 years
∴ Interest = P×R×T100=1200×12×3100
Amount = Principal + Interest
= ₹ 1200 + ₹ 432 = ₹ 1632
Hence, the required amount = ₹ 1632

(b) Given: Principal = ₹ 7500
Rate = 5% p.a.
Time = 3 years
∴ Interest = P×R×T100=7500×5×3100
= ₹1125
Amount = Principal + Interest
= ₹ 7500 + 11125 = ₹ 8625
Hence, the required amount = ₹ 8625.

Ex 8.3 Class 7 Maths Question 10.
What rate gives ₹ 280 as interest on a sum of ₹ 56,000 in 2 years?
Solution:
Given: Principal = ₹ 56,000
Interest = ₹280
Time = 2 years
Rate = ?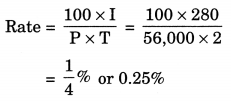

Hence, the required rate = 0.25%

Ex 8.3 Class 7 Maths Question 11.
If Meena gives an interest of ₹ 45 for one year at 9% rate p.a. What is the sum she has borrowed?
Solution:
Given: Interest = ₹ 45
Time = 1 year
Rate = 9% p.a.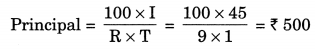

Hence, the required sum = ₹ 500.

Comparing Quantities Class 7 Extra Questions Maths Chapter 8

Extra Questions for Class 7 Maths Chapter 8 Comparing Quantities

Comparing Quantities Class 7 Extra Questions Very Short Answer Type

Question 1.
Find the ratio of:
(a) 5 km to 400 m
(b) 2 hours to 160 minutes
Solution:
(a) 5 km = 5 × 1000 = 5000 m
Ratio of 5 km to 400 m
= 5000 m : 400 m
= 25 : 2
Required ratio = 25 : 2
(b) 2 hours = 2 × 60 = 120 minutes
Ratio of 2 hours to 160 minutes
= 120 : 160
= 3 : 4
Required ratio = 3 : 4

Question 2.
State whether the following ratios are equivalent or not?
(a) 2 : 3 and 4 : 5
(b) 1 : 3 and 2 : 6
Solution:
(a) Given ratios = 2 : 3 and 4 : 5

Hence 2 : 3 and 4 : 5 are not equivalent ratios.
(b) Given ratios = 1 : 3 and 2 : 6
LCM of 3 and 6 = 6

Hence, 1 : 3 and 2 : 6 are equivalent ratios.

Question 3.
Express the following ratios in simplest form:
(a) 615 : 213
(b) 42 : 56
Solution:

Question 4.
Compare the following ratios:
3 : 4, 5 : 6 and 3 : 8
Solution:
Given: 3 : 4, 5 : 6 and 3 : 8
or 34 , 56 and 38
LCM of 4, 6 and 8 = 24

Hence, 3 : 8 < 3 : 4 < 5 : 6

Question 5.
State whether the following ratios are proportional or not:
(i) 20 : 45 and 4 : 9
(ii) 9 : 27 and 33 : 11
Solution:
(i) 20 : 45 and 4 : 9
Product of extremes = 20 × 9 = 180
Product of means = 45 × 4 = 180
Here, the product of extremes = Product of means
Hence, the given ratios are in proportion.
(ii) 9 : 27 and 33 : 11
Product of extremes = 9 × 11 = 99
Product of means = 27 × 33 = 891
Here, the product of extremes ≠ Product of means
Hence, the given ratios are not in proportion.

Question 6.
24, 36, x are in continued proportion, find the value of x.
Solution:
Since, 24, 36, x are in continued proportion.
24 : 36 :: 36 : x
⇒ 24 × x = 36 × 36
⇒ x = 54
Hence, the value of x = 54.

Question 7.
Find the mean proportional between 9 and 16.
Solution:
Let x be the mean proportional between 9 and 16.
9 : x :: x : 16
⇒ x × x = 9 × 16
⇒ x2 = 144
⇒ x = √144 = 12
Hence, the required mean proportional = 12.

Question 8.
Find:
(i) 36% of 400
(ii) 1623% of 32
Solution:

Question 9.
Find a number whose 614% is 12.
Solution:
Let the required number be x.

Hence, the required number = 192.

Question 10.
What per cent of 40 kg is 440 g?
Solution:
Let x% of 40 kg = 440 g

Hence, the required Percentage = 1.1%

Comparing Quantities Class 7 Extra Questions Short Answer Type

Question 11.
Convert each of the following into the decimal form:
(а) 25.2%
(b) 0.15%
(c) 25%
Solution:

Question 12.
What per cent of
(a) 64 is 148.48?
(b) 75 is 1225?
Solution:

Question 13.
A machine costs ₹ 7500. Its value decreases by 5% every year due to usage. What will be its price after one year?
Solution:
The cost price of the machine = ₹ 7500
Decrease in price = 5%
Decreased price after one year

= 75 × 95
= ₹ 7125
Hence, the required price = ₹ 7125.

Question 14.
What sum of money lent out at 12 per cent p.a. simple interest would produce ₹ 9000 as interest in 2 years?
Solution:
Here, Interest = ₹ 9000
Rate = 12% p.a.
Time = 2 years
Principal = ?

Hence, the required principal amount = ₹ 37500.

Question 15.
Rashmi obtains 480 marks out of 600. Rajan obtains 560 marks out of 700. Whose performance is better?
Solution:
Rashmi obtains 480 marks out of 600
Marks Percentage = 480600 × 100 = 80%
Rajan obtains 560 marks out of 700
Marks Percentage = 560700 × 100 = 80%
Since, both of them obtained the same per cent of marks i.e. 80%.
So, their performance cannot be compared.

Question 16.
₹ 9000 becomes ₹ 18000 at simple interest in 8 years. Find the rate per cent per annum.
Solution:
Here, Principal = ₹ 9000
Amount = ₹ 18000
Interest = Amount – Principal = ₹ 18000 – ₹ 9000 = ₹ 9000

Hence, the required rate of interest = 1212%.

Question 17.
The cost of an object is increased by 12%. If the current cost is ₹ 896, what was its original cost?
Solution:
Here, rate of increase in cost = 12%
Increased Cost = ₹ 896
Original Cost = ?
Let the Original Cost be ₹ x

Hence, the required cost = ₹ 800.

Comparing Quantities Class 7 Extra Questions Long Answer Type

Question 18.
Radhika borrowed ₹ 12000 from her friends. Out of which ₹ 4000 were borrowed at 18% and the remaining at 15% rate of interest per annum. What is the total interest after 3 years? (NCERT Exemplar)
Solution:
Total amount borrowed by Radhika = ₹ 12,000
The amount borrowed by her at 18% p.a. = ₹ 4000

Total interest = ₹ 2160 + ₹ 3600 = ₹ 5760
Hence, the total interest = ₹ 5760.

Question 19.
Bhavya earns ₹ 50,000 per month and spends 80% of it. Due to pay revision, her monthly income increases by 20% but due to price rise, she has to spend 20% more. Find her new savings. (NCERT Exemplar)
Solution:
Monthly income of Bhavya = ₹ 50,000
Money spent by her = 80% of ₹ 50,000
= 80100 × 50,000 = ₹ 40,000
Due to pay revision, income is increased by 20%

So, the new savings = ₹ 60,000 – ₹ 48,000 = ₹ 12,000

Question 20.
The simple interest on a certain sum at 5% per annum for 3 years and 4 years differ by ₹ 82. Find the sum.
Solution:
Let the required sum be ₹ P.
Simple interest for 3 years

Alternate Method
Simple Interest gained from 3rd to 4th year = ₹ 82
Time (4th year – 3rd year) = 1 year

Required sum = ₹ 1640

Comparing Quantities Class 7 Extra Questions Higher Order Thinking Skills (HOTS) Type

Question 21.
Rajan’s monthly income is 20% more than the monthly income of Sarita. What per cent of Sarita’s income is less than Rajan’s monthly income?
Solution:
Let the monthly income of Sarita be ₹ 100.
Rajan’s monthly income

Now, Sarita’s monthly income is less than the monthly income of Raj an by = ₹ 120 – ₹ 100 = ₹ 20
Per cent of less in Rajan’s monthly income
= 20×100120 = 503% = 1623%
Hence, the required per cent = 1623%

Question 22.
If 10 apples are bought for ₹ 11 and sold at the rate of 11 apples for ₹ 10. Find the overall gain or loss per cent in these transactions.
Solution:
CP of 10 apples = ₹ 11
CP of 1 apple = ₹ 1110
SP of 11 apples = ₹ 10
SP of 1 apple = ₹ 1011

Question 23.
If 25 men can do a work in 36 hours, find the number of men required to do the same work in 108 hours.
Solution:
Let the number of men required to be x.
Men : Hours :: Men : Hours
25 : 36 :: x : 108
Product of extremes = 25 × 108
Product of means = 36 × x
Product of means = Product of extremes
36 × x = 25 × 108
⇒ x = 25 × 3 = 75
Hence, the required number of men = 75.

Question 24.
A machine is sold by A to B at a profit of 10% and then B sold it to C at a profit of 20%. If C paid ₹ 1200 for the machine, what amount was paid by A to purchase the machine?
Solution:
Cost price of machine for C = Selling price of the machine for B = ₹ 1200

Hence, the required cost price = ₹ 9091011 or ₹ 909.09 (approx)