Class 8 Maths Chapter 3 Understanding Quadrilaterals All Exercise NCERT Solutions

Class 8 Maths Chapter 3 Understanding Quadrilaterals All Exercise NCERT Solutions

• Class 8 Maths Chapter Understanding Quadrilaterals Ex 3.1
• Class 8 Maths Chapter Understanding Quadrilaterals Ex 3.2
• Class 8 Maths Chapter Understanding Quadrilaterals Ex 3.3
• Class 8 Maths Chapter Understanding Quadrilaterals Ex 3.4

NCERT Solutions for Class 8 Maths Chapter 3 Understanding Quadrilaterals Ex 3.1

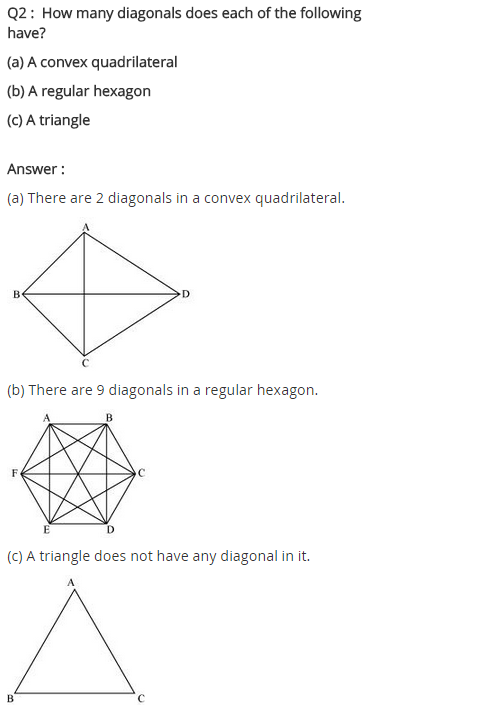
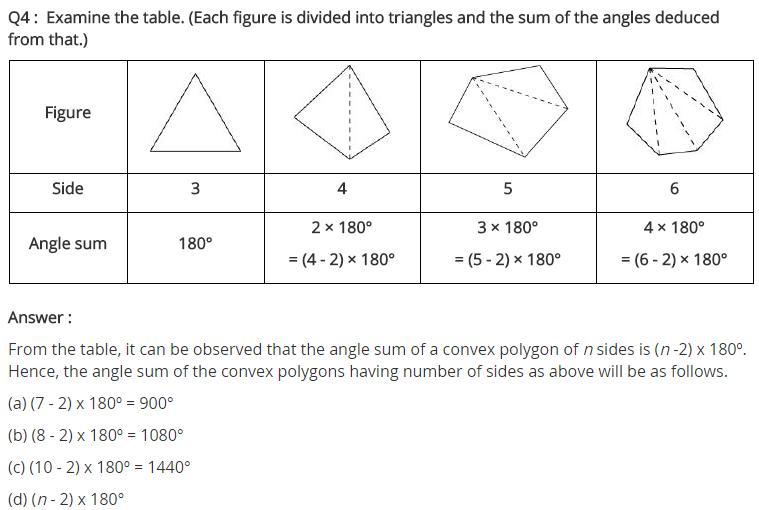
NCERT Solutions for Class 8 Maths Chapter 3 Understanding Quadrilaterals Exercise 3.2

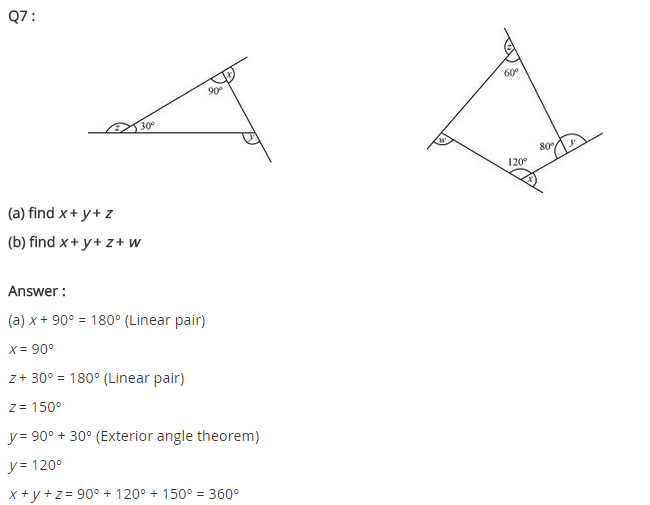
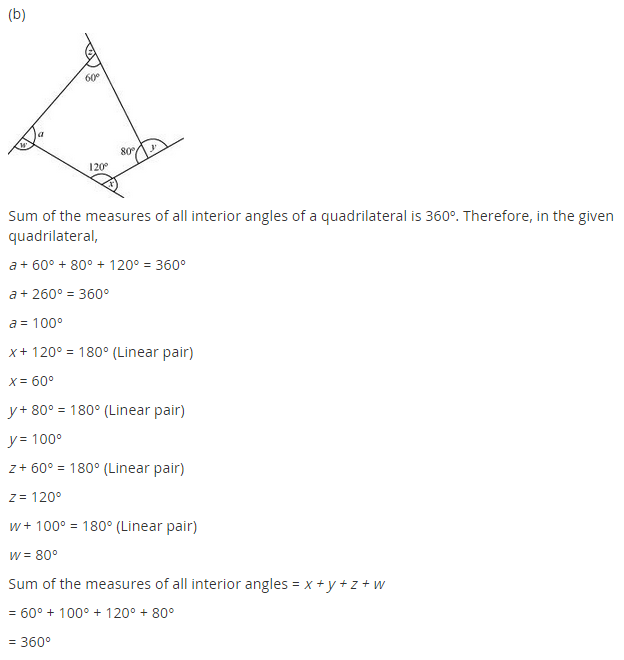
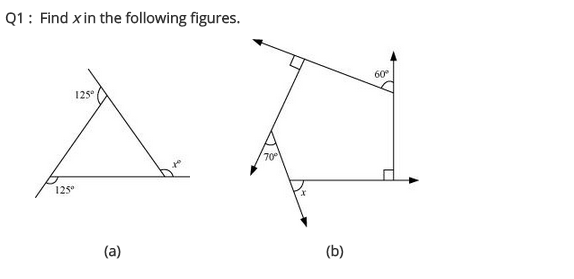
Ex 3.2 Class 8 Maths Question 1.
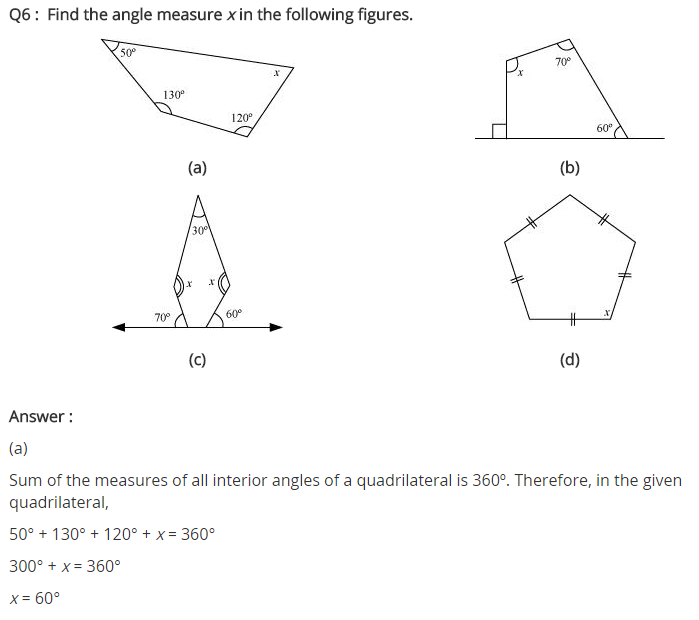
Find x in the following figures.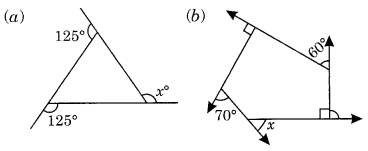

Solution:
(a) We know that the sum of all the exterior angles of a polygon = 360°
125° + 125° + x = 360°
⇒ 250° + x = 360°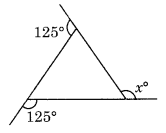

x = 360° – 250° = 110°
Hence x = 110°
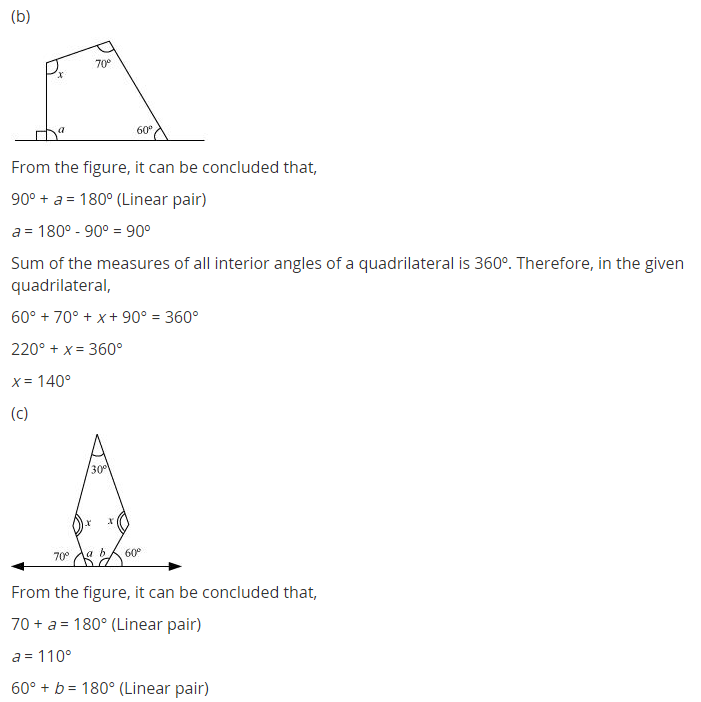
(b) Here ∠y = 180° – 90° = 90°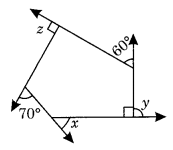

and ∠z = 90° (given)
x + y + 60° + z + 70° = 360° [∵ Sum of all the exterior angles of a polygon = 360°]
⇒ x + 90° + 60° + 90° + 70° = 360°
⇒ x + 310° = 360°
⇒ x = 360° – 310° = 50°
Hence x = 50°

Ex 3.2 Class 8 Maths Question 2.
Find the measure of each exterior angle of a regular polygon of
(i) 9 sides
(ii) 15 sides
Solution:
(i) We know the sum of all the exterior angles of polygon = 360°
Measure of each angle of 9 sided regular polygon = 3609 = 40°
(ii) Sum of all the exterior angles of a polygon = 360°
Measure of each angle of 15 sided regular polygon = 36015 = 24°

Ex 3.2 Class 8 Maths Question 3.
How many sides does a regular polygon have if the measure of an exterior angle is 24°?
Solution:
Sum of all exterior angles of a regular polygon = 360°
Number of sides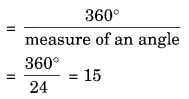

Hence, the number of sides = 15

Ex 3.2 Class 8 Maths Question 4.
How many sides does a regular polygon have if each of its interior angles is 165°?
Solution:
Let re be the number of sides of a regular polygon.
Sum of all interior angles = (n – 2) × 180°
and, measure of its each angle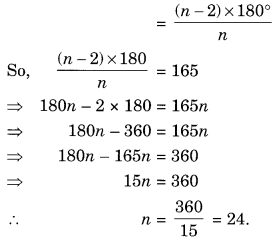

Hence, the number of sides = 24

Ex 3.2 Class 8 Maths Question 5.
(a) Is it possible to have a regular polygon with measure of each exterior angle a is 22°?
(b) Can it be an interior angle of a regular polygon? Why?
Solution:
(a) Since, the sum of all the exterior angles of a regular polygon = 360° which is not divisible by 22°.
It is not possible that a regular polygon must have its exterior angle 22°.
(b) Sum of all interior angles of a regular polygon of side n = (n – 2) × 180°

not a whole number.
Since number of sides cannot be in fractions.
It is not possible for a regular polygon to have its interior angle = 22°.

Ex 3.2 Class 8 Maths Question 6.
(a) What is the minimum interior angle possible for a regular polygon? Why?
(b) What is the maximum exterior angle possible for a regular polygon?
Solution:
(a) Sum of all interior angles of a regular polygon of side n = (n – 2) × 180°
The measure of each interior angle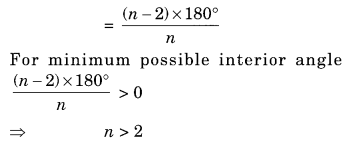

The minimum measure the angle of an equilateral triangle (n = 3) = 60°.
(b) From part (a) we can conclude that the maximum exterior angle of a regular polygon = 180° – 60° = 120°.

NCERT Solutions for Class 8 Maths Chapter 3 Understanding Quadrilaterals Exercise 3.3

Ex 3.3 Class 8 Maths Question 1.
Given a parallelogram ABCD. Complete each statement along with the definition or property used.
(i) AD = …………
(ii) ∠DCB = ………
(iii) OC = ………
(iv) m∠DAB + m∠CDA = ……..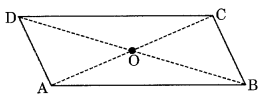

Solution:
(i) AD = BC [Opposite sides of a parallelogram are equal]
(ii) ∠DCB = ∠DAB [Opposite angles of a parallelogram are equal]
(iii) OC = OA [Diagonals of a parallelogram bisect each other]
(iv) m∠DAB + m∠CDA = 180° [Adjacent angles of a parallelogram are supplementary]

Ex 3.3 Class 8 Maths Question 2.
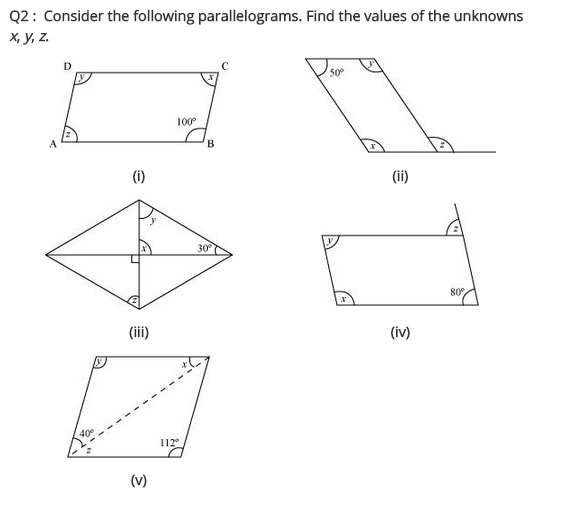
Consider the following parallelograms. Find the values of the unknowns x, y, z.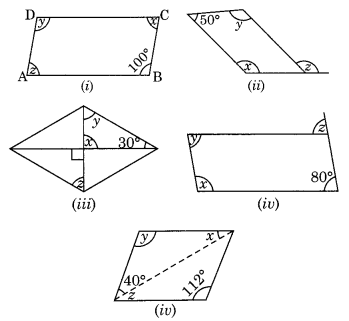

Solution:
(i) ABCD is a parallelogram.

∠B = ∠D [Opposite angles of a parallelogram are equal]
∠D = 100°
⇒ y = 100°
∠A + ∠B = 180° [Adjacent angles of a parallelogram are supplementary]
⇒ z + 100° = 180°
⇒ z = 180° – 100° = 80°
∠A = ∠C [Opposite angles of a ||gm]
x = 80°
Hence x = 80°, y = 100° and z = 80°
(ii) PQRS is a parallelogram.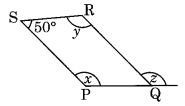

∠P + ∠S = 180° [Adjacent angles of parallelogram]
⇒ x + 50° = 180°
x = 180° – 50° = 130°
Now, ∠P = ∠R [Opposite angles are equal]
⇒ x = y
⇒ y = 130°
Also, y = z [Alternate angles]
z = 130°
Hence, x = 130°, y = 130° and z = 130°
(iii) ABCD is a rhombus.
[∵ Diagonals intersect at 90°]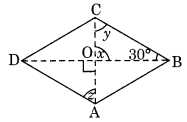

x = 90°
Now in ∆OCB,
x + y + 30° = 180° (Angle sum property)
⇒ 90° + y + 30° = 180°
⇒ y + 120° = 180°
⇒ y = 180° – 120° = 60°
y = z (Alternate angles)
⇒ z = 60°
Hence, x = 90°, y = 60° and z = 60°.
(iv) ABCD is a parallelogram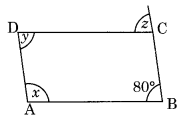

∠A + ∠B = 180° (Adjacent angles of a parallelogram are supplementary)
⇒ x + 80° = 180°
⇒ x = 180° – 80° = 100°
Now, ∠D = ∠B [Opposite angles of a |jgm]
⇒ y = 80°
Also, z = ∠B = 80° (Alternate angles)
Hence x = 100°, y = 80° and z = 80°
(v) ABCD is a parallelogram.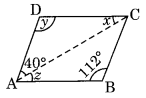

∠D = ∠B [Opposite angles of a ||gm]
y = 112°
x + y + 40° = 180° [Angle sum property]
⇒ x + 112° + 40° = 180°
⇒ x + 152° = 180°
⇒ x = 180° – 152 = 28°
z = x = 28° (Alternate angles)
Hence x = 28°, y = 112°, z = 28°.

Ex 3.3 Class 8 Maths Question 3.
Can a quadrilateral ABCD be a parallelogram if
(i) ∠D + ∠B = 180°?
(ii) AB = DC = 8 cm, AD = 4 cm and BC = 4.4 cm?
(iii) ∠A = 70° and ∠C = 65°?
Solution:
(i) For ∠D + ∠B = 180, quadrilateral ABCD may be a parallelogram if following conditions are also fulfilled.
(a) The sum of measures of adjacent angles should be 180°.
(b) Opposite angles should also be of same measures. So, ABCD can be but need not be a parallelogram.
(ii) Given: AB = DC = 8 cm, AD = 4 cm, BC = 4.4 cm
In a parallelogram, opposite sides are equal.
Here AD ≠ BC
Thus, ABCD cannot be a parallelogram.
(iii) ∠A = 70° and ∠C = 65°
Since ∠A ≠ ∠C
Opposite angles of quadrilateral are not equal.
Hence, ABCD is not a parallelogram.

Ex 3.3 Class 8 Maths Question 4.
Draw a rough figure of a quadrilateral that is not a parallelogram but has exactly two opposite angles of equal measure.
Solution:
ABCD is a rough figure of a quadrilateral in which m∠A = m∠C but it is not a parallelogram. It is a kite.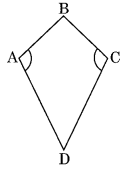

Ex 3.3 Class 8 Maths Question 5.
The measures of two adjacent angles of a parallelogram are in the ratio 3 : 2. Find the measure of each of the angles of the parallelogram.
Solution:
Let ABCD is parallelogram such that
m∠B : m∠C = 3 : 2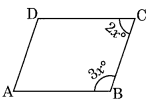

Let m∠B = 3x° and m∠C = 2x°
m∠B + m∠C = 180° (Sum of adjacent angles = 180°)
3x + 2x = 180°
⇒ 5x = 180°
⇒ x = 36°
Thus, ∠B = 3 × 36 = 108°
∠C = 2 × 36° = 72°
∠B = ∠D = 108°
and ∠A = ∠C = 72°
Hence, the measures of the angles of the parallelogram are 108°, 72°, 108° and 72°.

Ex 3.3 Class 8 Maths Question 6.
Two adjacent angles of a parallelogram have equal measure. Find the measure of each of the angles of the parallelogram.
Solution:
Let ABCD be a parallelogram in which
∠A = ∠B

We know ∠A + ∠B = 180° [Sum of adjacent angles = 180°]
∠A + ∠A = 180°
⇒ 2∠A = 180°
⇒ ∠A = 90°
Thus, ∠A = ∠C = 90° and ∠B = ∠D = 90°
[Opposite angles of a parallelogram are equal]

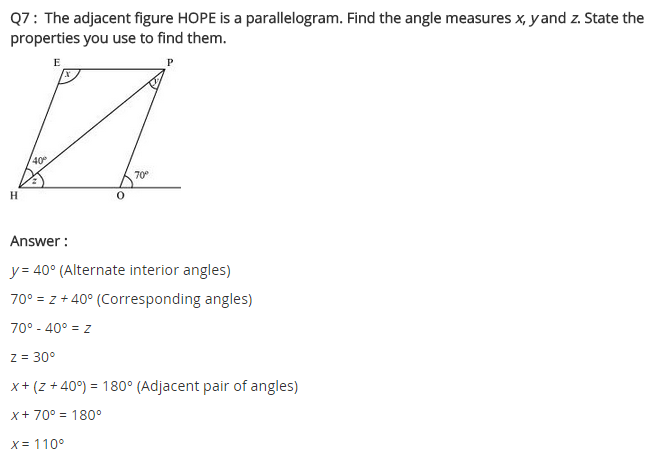
Ex 3.3 Class 8 Maths Question 7.
The adjacent figure HOPE is a parallelogram. Find the angle measures x, y and z. State the properties you use to find them.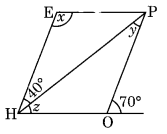

Solution:
∠y = 40° (Alternate angles)
∠z + 40° = 70° (Exterior angle property)
⇒ ∠z = 70° – 40° = 30°
z = ∠EPH (Alternate angle)
In ∆EPH
∠x + 40° + ∠z = 180° (Adjacent angles)
⇒ ∠x + 40° + 30° = 180°
⇒ ∠x + 70° = 180°
⇒ ∠x = 180° – 70° = 110°
Hence x = 110°, y = 40° and z = 30°.

Ex 3.3 Class 8 Maths Question 8.
The following figures GUNS and RUNS are parallelograms. Find x and y. (Lengths are in cm)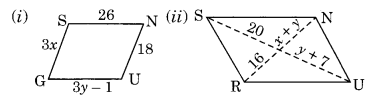

Solution:
(i) GU = SN (Opposite sides of a parallelogram)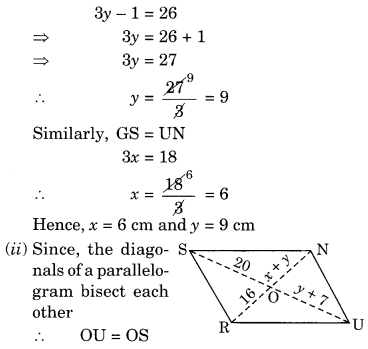

⇒ y + 7 = 20
⇒ y = 20 – 7 = 13
Also, ON = OR
⇒ x + y = 16
⇒ x + 13 = 16
x = 16 – 13 = 3
Hence, x = 3 cm and y = 13 cm.

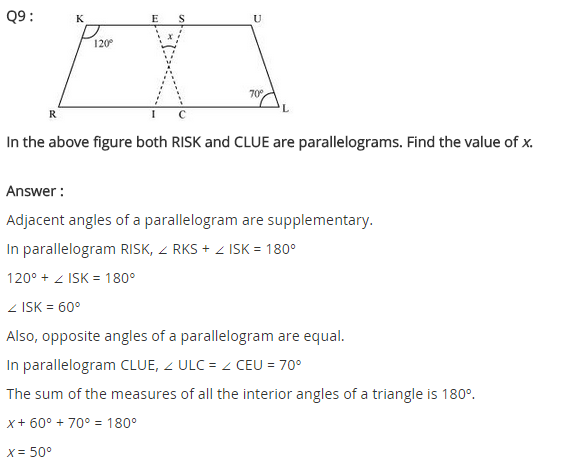
Ex 3.3 Class 8 Maths Question 9.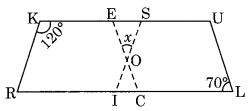

In the above figure both RISK and CLUE are parallelograms. Find the value of x.
Solution:
Here RISK and CLUE are two parallelograms.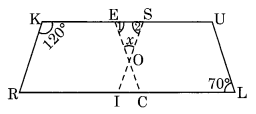

∠1 = ∠L = 70° (Opposite angles of a parallelogram)
∠K + ∠2 = 180°
Sum of adjacent angles is 180°
120° + ∠2 = 180°
∠2 = 180° – 120° = 60°
In ∆OES,
∠x + ∠1 + ∠2 = 180° (Angle sum property)
⇒ ∠x + 70° + 60° = 180°
⇒ ∠x + 130° = 180°
⇒ ∠x = 180° – 130° = 50°
Hence x = 50°

Ex 3.3 Class 8 Maths Question 10.
Explain how this figure is a trapezium. Which of its two sides are parallel?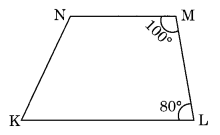

Solution:
∠M + ∠L = 100° + 80° = 180°
∠M and ∠L are the adjacent angles, and sum of adjacent interior angles is 180°
KL is parallel to NM
Hence KLMN is a trapezium.

Ex 3.3 Class 8 Maths Question 11.
Find m∠C in below figure if AB¯ || DC¯
Solution:
Given that AB¯ || DC¯
m∠B + m∠C = 180° (Sum of adjacent angles of a parallelogram is 180°)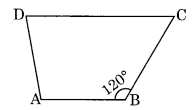

120° + m∠C = 180°
m∠C = 180° – 120° = 60°
Hence m∠C = 60°

Ex 3.3 Class 8 Maths Question 12.
Find the measure of ∠P and ∠S if 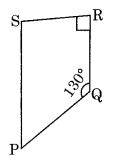SP¯ || RQ¯ in figure, is there any other method to find m∠P?)

Solution:
Given that ∠Q = 130° and ∠R = 90°
SP¯ || RQ¯ (given)
∠P + ∠Q = 180° (Adjacent angles)
⇒ ∠P + 130° = 180°
⇒ ∠P = 180° – 130° = 50°
and, ∠S + ∠R = 180° (Adjacent angles)
⇒ ∠S + 90° = 180°
⇒ ∠S = 180° – 90° = 90°
Alternate Method:
∠Q = 130°, ∠R = 90° and ∠S = 90°
We know that
∠P + ∠Q + ∠R + ∠Q = 360° (Angle sum property of quadrilateral)
⇒ ∠P + 130° + 90° + 90° = 360°
⇒ ∠P + 310° = 360°
⇒ ∠P = 360° – 310° = 50°
Hence m∠P = 50°

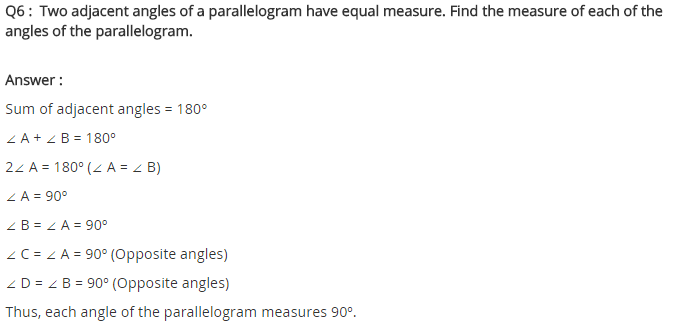
NCERT Solutions for Class 8 Maths Chapter 3 Understanding Quadrilaterals Exercise 3.4

Ex 3.4 Class 8 Maths Question 1.
State whether True or False.
(a) All rectangles are squares.
(b) All rhombuses are parallelograms.
(c) All squares are rhombuses and also rectangles.
(d) All squares are not parallelograms.
(e) All kites are rhombuses.
(f) All rhombuses are kites.
(g) All parallelograms are trapeziums.
(h) All squares are trapeziums.

Solution:
(a) False
(b) True
(c) True
(d) False
(e) False
(f) True
(g) True
(h) True

Ex 3.4 Class 8 Maths

Question 2.
Identify all the quadrilaterals that have
(a) four sides of equal length
(b) four right angles
Solution:
(a) Squares and rhombuses.
(b) Rectangles and squares.

Ex 3.4 Class 8 Maths

Question 3.
Explain how a square is
(i) a quadrilateral
(ii) a parallelogram
(iii) a rhombus
(iv) a rectangle
Solution:
(i) Square is a quadrilateral because it is closed with four line segments.
(ii) Square is a parallelogram due to the following properties:
(a) Opposite sides are equal and parallel.
(b) Opposite angles are equal.
(iii) Square is a rhombus because its all sides are equal and opposite sides are parallel.
(iv) Square is a rectangle because its opposite sides are equal and has equal diagonal.

Ex 3.4 Class 8 Maths

Question 4.
Name the quadrilaterals whose diagonals
(i) bisect each other
(ii) are perpendicular bisectors of each other
(iii) are equal
Solution:
(i) Parallelogram, rectangle, square and rhombus
(ii) Square and rhombus
(iii) Rectangle and square

Ex 3.4 Class 8 Maths 

Question 5.
Explain why a rectangle is a convex quadrilateral.
Solution:
In a rectangle, both of its diagonal lie in its interior. Hence, it is a convex quadrilateral.

Ex 3.4 Class 8 Maths 

Question 6.
ABC is a right-angled triangle and O is the midpoint of the side opposite to the right angle. Explain why O is equidistant from A, B and C. (The dotted lines are drawn additionally to help you).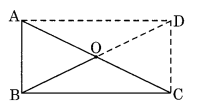

Solution:
Since the right-angled triangle ABC makes a rectangle ABCD by the dotted lines.
Therefore OA = OB = OC = OD [Diagonals of a rectangle are equal and bisect each other]
Hence, O is equidistant from A, B and C.

NCERT Solutions for Class 8 Maths

• Chapter 1 Rational Numbers
• Chapter 2 Linear Equations in One Variable
• Chapter 3 Understanding Quadrilaterals
• Chapter 4 Practical Geometry
• Chapter 5 Data Handling
• Chapter 6 Squares and Square Roots
• Chapter 7 Cubes and Cube Roots
• Chapter 8 Comparing Quantities
• Chapter 9 Algebraic Expressions and Identities
• Chapter 10 Visualising Solid Shapes
• Chapter 11 Mensuration
• Chapter 12 Exponents and Powers
• Chapter 13 Direct and Indirect proportions
• Chapter 14 Factorisation
• Chapter 15 Introduction to Graphs
• Chapter 16 Playing with Numbers