Class 8 Maths Chapter 6 Squares and Square Roots All Exercise NCERT Solutions

Class 8 Maths Chapter 6 Squares and Square Roots All Exercise NCERT Solutions

• Class 8 Maths Squares and Square Roots Exercise 6.1
• Class 8 Maths Squares and Square Roots Exercise 6.2
• Class 8 Maths Squares and Square Roots Exercise 6.3
• Class 8 Maths Squares and Square Roots Exercise 6.4

NCERT Solutions for Class 8 Maths Chapter 6 Squares and Square Roots Exercise 6.1

Ex 6.1 Class 8 Maths Question 1.
What will be the unit digit of the squares of the following numbers?
(i) 81
(ii) 272
(iii) 799
(iv) 3853
(v) 1234
(vi) 20387
(vii) 52698
(viii) 99880
(ix) 12796
(x) 55555
Solution:
(i) Unit digit of 812 = 1
(ii) Unit digit of 2722 = 4
(iii) Unit digit of 7992 = 1
(iv) Unit digit of 38532 = 9
(v) Unit digit of 12342 = 6
(vi) Unit digit of 263872 = 9
(vii) Unit digit of 526982 = 4
(viii) Unit digit of 998802 = 0
(ix) Unit digit of 127962 = 6
(x) Unit digit of 555552 = 5

Ex 6.1 Class 8 Maths Question 2.
The following numbers are not perfect squares. Give reason.
(i) 1057
(ii) 23453
(iii) 7928
(iv) 222222
(v) 64000
(vi) 89722
(vii) 222000
(viii) 505050
Solution:
(i) 1057 ends with 7 at unit place. So it is not a perfect square number.
(ii) 23453 ends with 3 at unit place. So it is not a perfect square number.
(iii) 7928 ends with 8 at unit place. So it is not a perfect square number.
(iv) 222222 ends with 2 at unit place. So it is not a perfect square number.
(v) 64000 ends with 3 zeros. So it cannot a perfect square number.
(vi) 89722 ends with 2 at unit place. So it is not a perfect square number.
(vii) 22000 ends with 3 zeros. So it can not be a perfect square number.
(viii) 505050 ends with 1 zero. So it is not a perfect square number.

Ex 6.1 Class 8 Maths Question 3.
The squares of which of the following would be odd numbers?
(i) 431
(ii) 2826
(iii) 7779
(iv) 82004
Solution:
(i) 4312 is an odd number.
(ii) 28262 is an even number.
(iii) 77792 is an odd number.
(iv) 820042 is an even number.

Ex 6.1 Class 8 Maths Question 4.
Observe the following pattern and find the missing digits.
112 = 121
1012 = 10201
10012 = 1002001
1000012 = 1…2…1
100000012 = ………
Solution:
According to the above pattern, we have
1000012 = 10000200001
100000012 = 100000020000001

Ex 6.1 Class 8 Maths Question 5.
Observe the following pattern and supply the missing numbers.
112 = 121
1012 = 10201
101012 = 102030201
10101012 = ……….
……….2 = 10203040504030201
Solution:
According to the above pattern, we have
10101012 = 1020304030201
1010101012 = 10203040504030201

Ex 6.1 Class 8 Maths Question 6.
Using the given pattern, find the missing numbers.
12 + 22 + 22 = 32
22 + 32 + 62 = 72
32 + 42 + 122 = 132
42 + 52 + ….2 = 212
52 + ….2 + 302 = 312
62 + 72 + …..2 = ……2
Solution:
According to the given pattern, we have
42 + 52 + 202 = 212
52 + 62 + 302 = 312
62 + 72 + 422 = 432

Ex 6.1 Class 8 Maths Question 7.
Without adding, find the sum.
(i) 1 + 3 + 5 + 7 + 9
(ii) 1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 + 19
(iii) 1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 + 19 + 21 + 23
Solution:
We know that the sum of n odd numbers = n2
(i) 1 + 3 + 5 + 7 + 9 = (5)2 = 25 [∵ n = 5]
(ii) 1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 + 19 = (10)2 = 100 [∵ n = 10]
(iii) 1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 + 19 + 21 + 23 = (12)2 = 144 [∵ n = 12]

Ex 6.1 Class 8 Maths Question 8.
(i) Express 49 as the sum of 7 odd numbers.
(ii) Express 121 as the sum of 11 odd numbers.
Solution:
(i) 49 = 1 + 3 + 5 + 7 + 9 + 11 + 13 (n = 7)
(ii) 121 = 1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 + 19 + 21 (n = 11)

Ex 6.1 Class 8 Maths Question 9.
How many numbers lie between squares of the following numbers?
(i) 12 and 13
(ii) 25 and 26
(iii) 99 and 100.
Solution:
(i) We know that numbers between n2 and (n + 1)2 = 2n
Numbers between 122 and 132 = (2n) = 2 × 12 = 24
(ii) Numbers between 252 and 262 = 2 × 25 = 50 (∵ n = 25)
(iii) Numbers between 992 and 1002 = 2 × 99 = 198 (∵ n = 99)

NCERT Solutions for Class 8 Maths Chapter 6 Squares and Square Roots Exercise 6.2

Ex 6.2 Class 8 Maths Question 1.
Find the square of the following numbers.
(i) 32
(ii) 35
(iii) 86
(iv) 93
(v) 71
(vi) 46
Solution:
(i) 32 = 30 + 2
(32)2 = (30 + 2)2
= 30(30 + 2) + 2(30 + 2)
= 302 + 30 × 2 + 2 × 30 + 22
= 900 + 60 + 60 + 4
= 1024
Thus (32)2 = 1024

(ii) 35 = (30 + 5)
(35)2 = (30 + 5)2
= 30(30 + 5) + 5(30 + 5)
= (30)2 + 30 × 5 + 5 × 30 + (5)2
= 900 + 150 + 150 + 25
= 1225
Thus (35)2 = 1225

(iii) 86 = (80 + 6)
862 = (80 + 6)2
= 80(80 + 6) + 6(80 + 6)
= (80)2 + 80 × 6 + 6 × 80 + (6)2
= 6400 + 480 + 480 + 36
= 7396
Thus (86)2 = 7396

(iv) 93 = (90+ 3)
932 = (90 + 3)2
= 90 (90 + 3) + 3(90 + 3)
= (90)2 + 90 × 3 + 3 × 90 + (3)2
= 8100 + 270 + 270 + 9
= 8649
Thus (93)2 = 8649

(v) 71 = (70 + 1)
712 = (70 + 1)2
= 70 (70 + 1) + 1(70 + 1)
= (70)2 + 70 × 1 + 1 × 70 + (1)2
= 4900 + 70 + 70 + 1
= 5041
Thus (71)2 = 5041

(vi) 46 = (40+ 6)
462 = (40 + 6)2
= 40 (40 + 6) + 6(40 + 6)
= (40)2 + 40 × 6 + 6 × 40 + (6)2
= 1600 + 240 + 240 + 36
= 2116
Thus (46)2 = 2116

Ex 6.2 Class 8 Maths Question 2.
Write a Pythagorean triplet whose one member is
(i) 6
(ii) 14
(iii) 16
(iv) 18
Solution:
(i) Let m2 – 1 = 6
[Triplets are in the form 2m, m2 – 1, m2 + 1]
m2 = 6 + 1 = 7
So, the value of m will not be an integer.
Now, let us try for m2 + 1 = 6
⇒ m2 = 6 – 1 = 5
Also, the value of m will not be an integer.
Now we let 2m = 6 ⇒ m = 3 which is an integer.
Other members are:
m2 – 1 = 32 – 1 = 8 and m2 + 1 = 32 + 1 = 10
Hence, the required triplets are 6, 8 and 10

(ii) Let m2 – 1 = 14 ⇒ m2 = 1 + 14 = 15
The value of m will not be an integer.
Now take 2m = 14 ⇒ m = 7 which is an integer.
The member of triplets are 2m = 2 × 7 = 14
m2 – 1 = (7)2 – 1 = 49 – 1 = 48
and m2 + 1 = (7)2 + 1 = 49 + 1 = 50
i.e., (14, 48, 50)

(iii) Let 2m = 16 m = 8
The required triplets are 2m = 2 × 8 = 16
m2 – 1 = (8)2 – 1 = 64 – 1 = 63
m2 + 1 = (8)2 + 1 = 64 + 1 = 65
i.e., (16, 63, 65)

(iv) Let 2m = 18 ⇒ m = 9
Required triplets are:
2m = 2 × 9 = 18
m2 – 1 = (9)2 – 1 = 81 – 1 = 80
and m2 + 1 = (9)2 + 1 = 81 + 1 = 82
i.e., (18, 80, 82)

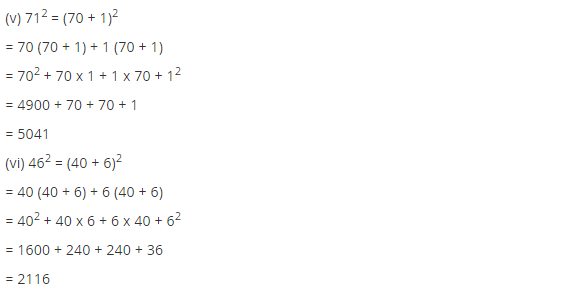
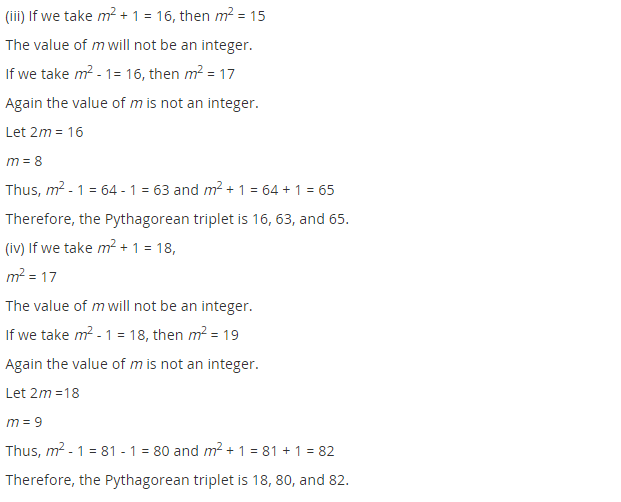
NCERT Solutions for Class 8 Maths Chapter 6 Squares and Square Roots Exercise 6.3

Ex 6.3 Class 8 Maths Question 1.
What could be the possible ‘one’s’ digits of the square root of each of the following numbers?
(i) 9801
(ii) 99856
(iii) 998001
(iv) 657666025
Solution:
(i) One’s digit in the square root of 9801 maybe 1 or 9.
(ii) One’s digit in the square root of 99856 maybe 4 or 6.
(iii) One’s digit in the square root of 998001 maybe 1 or 9.
(iv) One’s digit in the square root of 657666025 can be 5.

Ex 6.3 Class 8 Maths Question 2.
Without doing any calculation, find the numbers which are surely not perfect squares.
(i) 153
(ii) 257
(iii) 408
(iv) 441
Solution:
We know that the numbers ending with 2, 3, 7 or 8 are not perfect squares.
(i) 153 is not a perfect square number. (ending with 3)
(ii) 257 is not a perfect square number. (ending with 7)
(iii) 408 is not a perfect square number. (ending with 8)
(iv) 441 is a perfect square number.

Ex 6.3 Class 8 Maths Question 3.
Find the square roots of 100 and 169 by the method of repeated subtraction.
Solution:
Using the method of repeated subtraction of consecutive odd numbers, we have
(i) 100 – 1 = 99, 99 – 3 = 96, 96 – 5 = 91, 91 – 7 = 84, 84 – 9 = 75, 75 – 11 = 64, 64 – 13 = 51, 51 – 15 = 36, 36 – 17 = 19, 19 – 19 = 0
(Ten times repetition)
Thus √100 = 10

(ii) 169 – 1 = 168, 168 – 3 = 165, 165 – 5 = 160, 160 – 7 = 153, 153 – 9 = 144, 144 – 11 = 133, 133 – 13 = 120, 120 – 15 = 105, 105 – 17 = 88, 88 – 19 = 69, 69 – 21 = 48, 48 – 23 = 25, 25 – 25 = 0
(Thirteen times repetition)
Thus √169 = 13

Ex 6.3 Class 8 Maths Question 4.
Find the square roots of the following numbers by the prime factorisation Method.
(i) 729
(ii) 400
(iii) 1764
(iv) 4096
(v) 7744
(vi) 9604
(vii) 5929
(viii) 9216
(ix) 529
(x) 8100
Solution:
(i) We have 729
Prime factors of 729
729 = 3 × 3 × 3 × 3 × 3 × 3 = 32 × 32 × 32
√729 = 3 × 3 × 3 = 27

(ii) We have 400
Prime factors of 400
400 = 2 × 2 × 2 × 2 × 5 × 5 = 22 × 22 × 52
√400 = 2 × 2 × 5 = 20

(iii) 1764
1764 = 2 × 2 × 3 × 3 × 7 × 7 = 22 × 32 × 72
√1764 = 2 × 3 × 7 = 42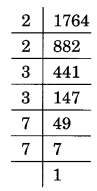

(iv) 4096
4096 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2
= 22 × 22 × 22 × 22 × 22 × 22
√4096 = 2 × 2 × 2 × 2 × 2 × 2 = 64

(v) Prime factorisation of 7744 is
7744 = 2 × 2 × 2 × 2 × 2 × 2 × 11 × 11
= 22 × 22 × 22 × 112
√7744 = 2 × 2 × 2 × 11 = 88

(vi) Prime factorisation of 9604 is
9604 = 2 × 2 × 7 × 7 × 7 × 7 = 22 × 72 × 72
√9604 = 2 × 7 × 7 = 98

(vii) Prime factorisation of 5929 is
5929 = 7 × 7 × 11 × 11 = 72 × 112
√5929 = 7 × 11 = 77

(viii) Prime factorisation of 9216 is
9216 = 2 × 2 × 2 × 2 × 2 × 2 ×2 × 2 × 2 × 2 × 3 × 3
= 22 × 22 × 22 × 22 × 22 × 32
√9216 = 2 × 2 × 2 × 2 × 2 × 3 = 96

(ix) Prime factorisation of 529 is
529 = 23 × 23 = 232
√529 = 23

(x) Prime factorisation of 8100 is
8100 = 2 × 2 × 3 × 3 × 3 × 3 × 5 × 5 = 22 × 32 × 32 × 52
√8100 = 2 × 3 × 3 × 5 = 90

Ex 6.3 Class 8 Maths Question 5.
For each of the following numbers, find the smallest whole number by which it should be multiplied so as to get a perfect square number. Also, find the square root of the square number so obtained.
(i) 252
(ii) 180
(iii) 1008
(iv) 2028
(v) 1458
(vi) 768
Solution:
(i) Prime factorisation of 252 is
252 = 2 × 2 × 3 × 3 × 7
Here, the prime factorisation is not in pair. 7 has no pair.
Thus, 7 is the smallest whole number by which the given number is multiplied to get a perfect square number.
The new square number is 252 × 7 = 1764
Square root of 1764 is
√1764 = 2 × 3 × 7 = 42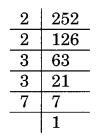

(ii) Primp factorisation of 180 is
180 = 2 × 2 × 3 × 3 × 5
Here, 5 has no pair.
New square number = 180 × 5 = 900
The square root of 900 is
√900 = 2 × 3 × 5 = 30
Thus, 5 is the smallest whole number by which the given number is multiplied to get a square number.

(iii) Prime factorisation of 1008 is
1008 = 2 × 2 × 2 × 2 × 3 × 3 × 7
Here, 7 has no pair.
New square number = 1008 × 7 = 7056
Thus, 7 is the required number.
Square root of 7056 is
√7056 = 2 × 2 × 3 × 7 = 84

(iv) Prime factorisation of 2028 is
2028 = 2 × 2 × 3 × 13 × 13
Here, 3 is not in pair.
Thus, 3 is the required smallest whole number.
New square number = 2028 × 3 = 6084
Square root of 6084 is
√6084 = 2 × 13 × 3 = 78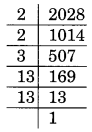

(v) Prime factorisation of 1458 is
1458 = 2 × 3 × 3 × 3 × 3 × 3 × 3
Here, 2 is not in pair.
Thus, 2 is the required smallest whole number.
New square number = 1458 × 2 = 2916
Square root of 1458 is
√2916 = 3 × 3 × 3 × 2 = 54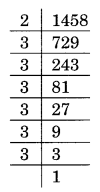

(vi) Prime factorisation of 768 is
768 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 3
Here, 3 is not in pair.
Thus, 3 is the required whole number.
New square number = 768 × 3 = 2304
Square root of 2304 is
√2304 = 2 × 2 × 2 × 2 × 3 = 48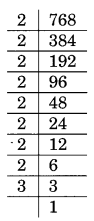

Ex 6.3 Class 8 Maths Question 6.
For each of the following numbers, find the smallest whole number by which it should be divided so as to get a perfect square. Also, find the square root of the square number so obtained.
(i) 252
(ii) 2925
(iii) 396
(iv) 2645
(v) 2800
(vi) 1620
Solution:
(i) Prime factorisation of 252 is
252 = 2 × 2 × 3 × 3 × 7
Here 7 has no pair.
7 is the smallest whole number by which 252 is divided to get a square number.
New square number = 252 ÷ 7 = 36
Thus, √36 = 6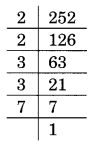

(ii) Prime factorisation of 2925 is
2925 = 3 × 3 × 5 × 5 × 13
Here, 13 has no pair.
13 is the smallest whole number by which 2925 is divided to get a square number.
New square number = 2925 ÷ 13 = 225
Thus √225 = 15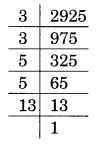

(iii) Prime factorisation of 396 is
396 = 2 × 2 × 3 × 3 × 11
Here 11 is not in pair.
11 is the required smallest whole number by which 396 is divided to get a square number.
New square number = 396 ÷ 11 = 36
Thus √36 = 6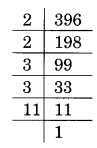

(iv) Prime factorisation of 2645 is
2645 = 5 × 23 × 23
Here, 5 is not in pair.
5 is the required smallest whole number.
By which 2645 is multiplied to get a square number
New square number = 2645 ÷ 5 = 529
Thus, √529 = 23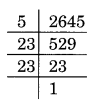

(v) Prime factorisation of 2800 is
2800 = 2 × 2 × 2 × 2 × 5 × 5 × 7
Here, 7 is not in pair.
7 is the required smallest number.
By which 2800 is multiplied to get a square number.
New square number = 2800 ÷ 7 = 400
Thus √400 = 20

(vi) Prime factorisation of 1620 is
1620 = 2 × 2 × 3 × 3 × 3 × 3 × 5
Here, 5 is not in pair.
5 is the required smallest prime number.
By which 1620 is multiplied to get a square number = 1620 ÷ 5 = 324
Thus √324 = 18

Ex 6.3 Class 8 Maths Question 7.
The students of class VIII of a school donated ₹ 2401 in all, for Prime Minister’s National Relief Fund. Each student donated as many rupees as the number of students in the class. Find the number of students in the class.
Solution:
Total amount of money donated = ₹ 2401
Total number of students in the class = √2401
= 72×72−−−−−−√
= 7×7×7×7−−−−−−−−−−√
= 7 × 7
= 49

Ex 6.3 Class 8 Maths Question 8.
2025 plants are to be planted in a garden in such a way that each row contains as many plants as the number of rows. Find the number of rows and the number of plants in each row.
Solution:
Total number of rows = Total number of plants in each row = √2025
= 3×3×3×3×5×5−−−−−−−−−−−−−−−−√
= 32×32×52−−−−−−−−−−√
= 3 × 3 × 5
= 45
Thus the number of rows and plants = 45

Ex 6.3 Class 8 Maths Question 9.
Find the smallest square number that is divisible by each of the numbers 4, 9 and 10.
Solution:
LCM of 4, 9, 10 = 180
The least number divisible by 4, 9 and 10 = 180
Now prime factorisation of 180 is
180 = 2 × 2 × 3 × 3 × 5
Here, 5 has no pair.
The required smallest square number = 180 × 5 = 900

Ex 6.3 Class 8 Maths Question 10.
Find the smallest number that is divisible by each of the numbers 8, 15 and 20.
Solution:
The smallest number divisible by 8, 15 and 20 is equal to their LCM.
LCM = 2 × 2 × 2 × 3 × 5 = 120
Here, 2, 3 and 5 have no pair.
The required smallest square number = 120 × 2 × 3 × 5 = 120 × 30 = 3600

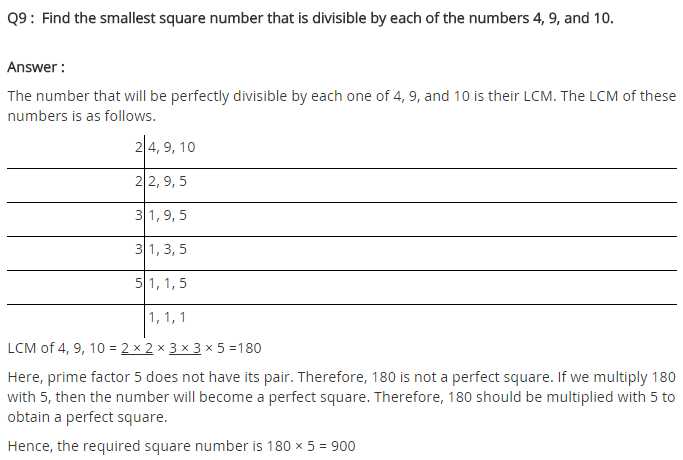
NCERT Solutions for Class 8 Maths Chapter 6 Squares and Square Roots Exercise 6.4

Ex 6.4 Class 8 Maths Question 1.
Find the square root of each of the following numbers by Long Division method.
(i) 2304
(ii) 4489
(iii) 3481
(iv) 529
(v) 3249
(vi) 1369
(vii) 5776
(viii) 7921
(ix) 576
(x) 1024
(xi) 3136
(xii) 900
Solution: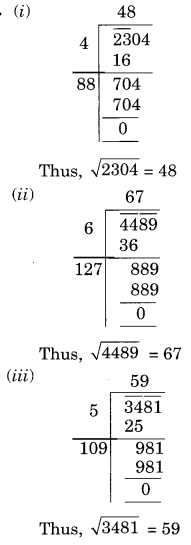

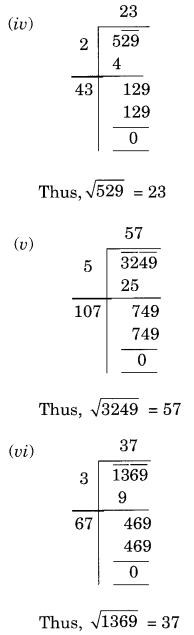
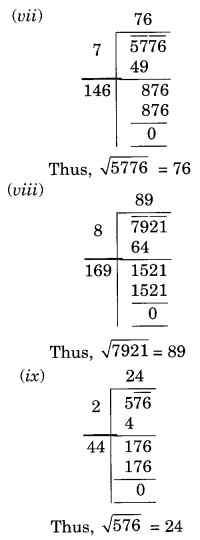
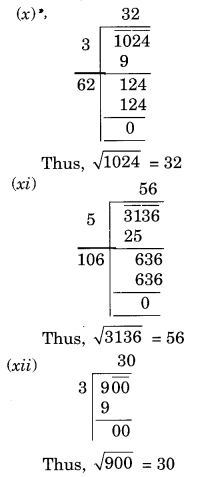
Ex 6.4 Class 8 Maths Question 2.
Find the number of digits in the square root of each of the following numbers (without any calculation)
(i) 64
(ii) 144
(iii) 4489
(iv) 27225
(v) 390625
Solution:
We know that if n is number of digits in a square number then
Number of digits in the square root = n2 if n is even and n+12 if n is odd.
(i) 64
Here n = 2 (even)
Number of digits in √64 = 22 = 1
(ii) 144
Here n = 3 (odd)
Number of digits in square root = 3+12 = 2
(iii) 4489
Here n = 4 (even)
Number of digits in square root = 42 = 2
(iv) 27225
Here n = 5 (odd)
Number of digits in square root = 5+12 = 3
(iv) 390625
Here n = 6 (even)
Number of digits in square root = 62 = 3

Ex 6.4 Class 8 Maths Question 3.
Find the square root of the following decimal numbers.
(i) 2.56
(ii) 7.29
(iii) 51.84
(iv) 42.25
(v) 31.36
Solution: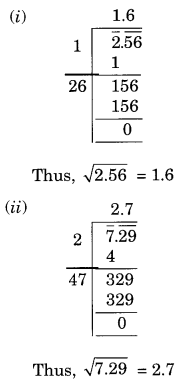

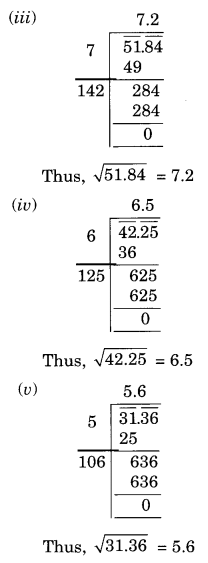
Ex 6.4 Class 8 Maths Question 4.
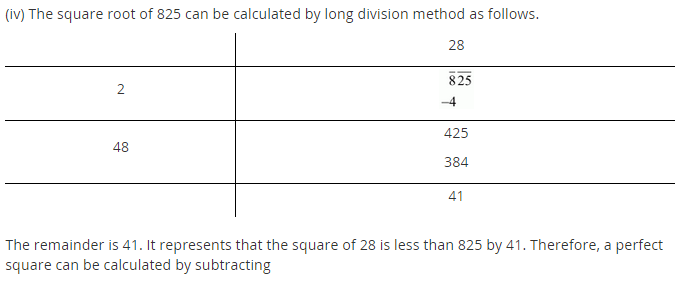
Find the least number which must be subtracted from each of the following numbers so as to get a perfect square. Also find the square root of the perfect square so obtained.
(i) 402
(ii) 1989
(iii) 3250
(iv) 825
(v) 4000
Solution:
(i)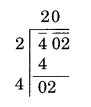

Here remainder is 2
2 is the least required number to be subtracted from 402 to get a perfect square
New number = 402 – 2 = 400
Thus, √400 = 20

(ii)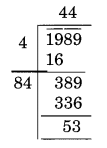

Here remainder is 53
53 is the least required number to be subtracted from 1989.
New number = 1989 – 53 = 1936
Thus, √1936 = 44

(iii)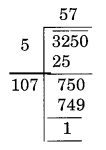

Here remainder is 1
1 is the least required number to be subtracted from 3250 to get a perfect square.
New number = 3250 – 1 = 3249
Thus, √3249 = 57

(iv)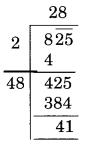

Here, the remainder is 41
41 is the least required number which can be subtracted from 825 to get a perfect square.
New number = 825 – 41 = 784
Thus, √784 = 28

(v)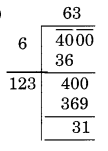

Here, the remainder is 31
31 is the least required number which should be subtracted from 4000 to get a perfect square.
New number = 4000 – 31 = 3969
Thus, √3969 = 63

Ex 6.4 Class 8 Maths Question 5.
Find the least number which must be added to each of the following numbers so as to get a perfect square. Also, find the square root of the perfect square so obtained.
(i) 525
(ii) 1750
(iii) 252
(iv) 1825
(v) 6412
Solution:
(i)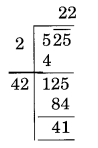

Here remainder is 41
It represents that square of 22 is less than 525.
Next number is 23 an 232 = 529
Hence, the number to be added = 529 – 525 = 4
New number = 529
Thus, √529 = 23

(ii)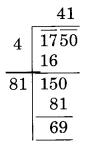

Here the remainder is 69
It represents that square of 41 is less than in 1750.
The next number is 42 and 422 = 1764
Hence, number to be added to 1750 = 1764 – 1750 = 14
Require perfect square = 1764
√1764 = 42

(iii)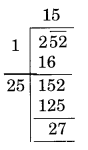

Here the remainder is 27.
It represents that a square of 15 is less than 252.
The next number is 16 and 162 = 256
Hence, number to be added to 252 = 256 – 252 = 4
New number = 252 + 4 = 256
Required perfect square = 256
and √256 = 16

(iv)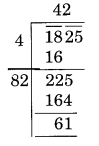

The remainder is 61.
It represents that square of 42 is less than in 1825.
Next number is 43 and 432 = 1849
Hence, number to be added to 1825 = 1849 – 1825 = 24
The required perfect square is 1848 and √1849 =43

(v)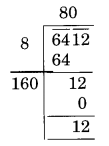

Here, the remainder is 12.
It represents that a square of 80 is less than in 6412.
The next number is 81 and 812 = 6561
Hence the number to be added = 6561 – 6412 = 149
The require perfect square is 6561 and √6561 = 81

Ex 6.4 Class 8 Maths Question 6.
Find the length of the side of a square whose area = 441 m2
Solution:
Let the length of the side of the square be x m.
Area of the square = (side)2 = x2 m2
x2 = 441 ⇒ x = √441 = 21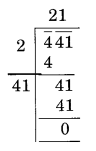

Thus, x = 21 m.
Hence the length of the side of square = 21 m.

Ex 6.4 Class 8 Maths Question 7.
In a right triangle ABC, ∠B = 90°.
(a) If AB = 6 cm, BC = 8 cm, find AC
(b) If AC = 13 cm, BC = 5 cm, find AB
Solution:
(a) In right triangle ABC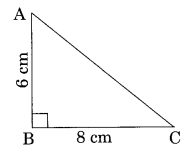

AC2 = AB2 + BC2 [By Pythagoras Theorem]
⇒ AC2 = (6)2 + (8)2 = 36 + 64 = 100
⇒ AC = √100 = 10
Thus, AC = 10 cm.
(b) In right triangle ABC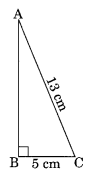

AC2 = AB2 + BC2 [By Pythagoras Theorem]
⇒ (13)2 = AB2 + (5)2
⇒ 169 = AB2 + 25
⇒ 169 – 25 = AB2
⇒ 144 = AB2
AB = √144 = 12 cm
Thus, AB = 12 cm.

Ex 6.4 Class 8 Maths Question 8.
A gardener has 1000 plants. He wants to plant these in such a way that the number of rows and the number of columns remain the same. Find the minimum number of plants he needs more for this.
Solution:
Let the number of rows be x.
And the number of columns also be x.
Total number of plants = x × x = x2
x2 = 1000 ⇒ x = √1000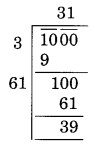

Here the remainder is 39
So the square of 31 is less than 1000.
Next number is 32 and 322 = 1024
Hence the number to be added = 1024 – 1000 = 24
Thus the minimum number of plants required by him = 24.
Alternative method: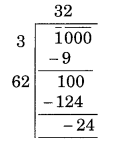

The minimum number of plants required by him = 24.

Ex 6.4 Class 8 Maths Question 9.
There are 500 children in a school. For a P.T. drill, they have to stand in such a manner that the number of rows is equal to the number of columns. How many children would be left out in this arrangement?
Solution:
Let the number of children in a row be x. And also that of in a column be x.
Total number of students = x × x = x2
x2 = 500 ⇒ x = √500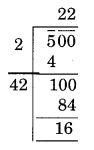

Here the remainder is 16
New Number 500 – 16 = 484
and, √484 = 22
Thus, 16 students will be left out in this arrangement.

NCERT Solutions for Class 8 Maths

• Chapter 1 Rational Numbers
• Chapter 2 Linear Equations in One Variable
• Chapter 3 Understanding Quadrilaterals
• Chapter 4 Practical Geometry
• Chapter 5 Data Handling
• Chapter 6 Squares and Square Roots
• Chapter 7 Cubes and Cube Roots
• Chapter 8 Comparing Quantities
• Chapter 9 Algebraic Expressions and Identities
• Chapter 10 Visualising Solid Shapes
• Chapter 11 Mensuration
• Chapter 12 Exponents and Powers
• Chapter 13 Direct and Indirect proportions
• Chapter 14 Factorisation
• Chapter 15 Introduction to Graphs
• Chapter 16 Playing with Numbers