Class 10 Maths Chapter 1 Real Numbers (Hindi + English) All Exercise NCERT Solution

Class 10 Maths Chapter 1 Real Numbers (Hindi + English) All Exercise NCERT Solution 

Table Of Content

• Ex.1.1
• Ex.1.2
• Ex.1.3
• Ex.1.4
• Real Numbers Class 10 Extra Questions
• Real Numbers Class 10 Important Questions
• Real Numbers Class 10 Notes

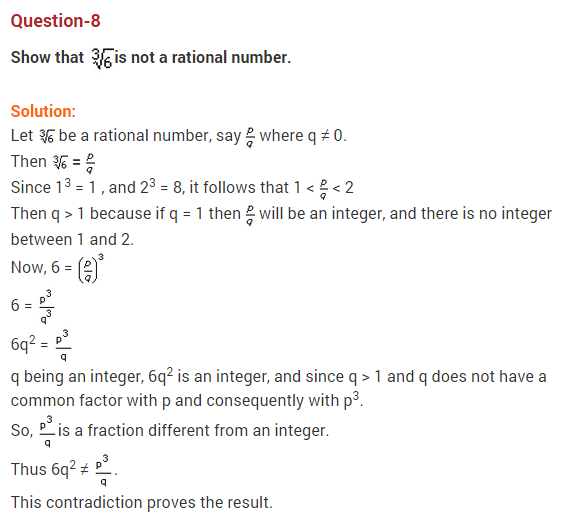
Ex 1.1 Class 10 Maths Question 1.
Use Euclid’s Division Algorithm to find the HCF of:
(i) 135 and 225
(ii) 196 and 38220
(iii) 867 and 255
Solution:

Ex 1.1 Class 10 Maths Question 2.
Show that any positive odd integer is of the form 6q + 1, or 6q + 3, or 6q + 5, where q is some integer.
Solution

Ex 1.1 Class 10 Maths Question 3.
An army contingent of 616 members is to march behind an army band of 32 members in a parade. The two groups are to march in the same number of columns. What is the maximum number of columns in which they can march?
Solution:

Ex 1.1 Class 10 Maths Question 4.
Use Euclid’s division lemma to show that the square of any positive integer is either of the form 3m or 3m + 1 for some integer m.
Solution:

Ex 1.1 Class 10 Maths Question 5.
Use Euclid’s Division Lemma to show that the cube of any positive integer is either of the form 9m, 9m + 1 or 9m + 8.
Solution: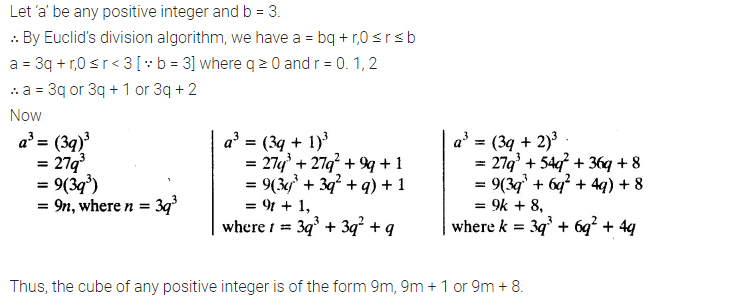

Class 10 Maths Real Numbers

Rational numbers and irrational numbers are taken together form the set of real numbers. The set of real numbers is denoted by R. Thus every real number is either a rational number or an irrational number. In either case, it has a non–terminating decimal representation. In the case of rational numbers, the decimal representation is repeating (including repeating zeroes) and if the decimal representation is non–repeating, it is an irrational number. For every real number, there corresponds a unique point on the number line ‘l’ or we may say that every point on the line ‘l’ corresponds to a real number (rational or irrational).

From the above discussion we may conclude that:
To every real number there corresponds a unique point on the number line and conversely, to every point on the number line there corresponds a real number. Thus we see that there is one–to–one correspondence between the real numbers and points on the number line ‘l’, that is why the number line is called the ‘real number line’.

NCERT Solutions for Class 10 Maths Chapter 1 Real Numbers (Hindi Medium) Ex 1.1

Real Numbers Class 10 Maths Objectives

The students will be able to ;
prove Euclid’s Division Lemma
state fundamental theorem of arithmetic
find HCF and LCM using prime factorization
establish the given number as an irrational number
conclude the decimal expansion of a rational number is either terminating or non-terminating repeating.

Chapter 1 Class 10 Maths Real Numbers Summary

We have studied the following points:
1. Euclid’s Division Lemma: Given positive integers a and b, there exist whole numbers q and r satisfying a = bq + r where 0 = r = b.
2. Euclid’s Division Algorithm: According to this, which is based on Euclid’s division lemma, the HCF of any two positive integers a and b with a > b is obtained as follows:
Step 1 Apply the division lemma to find q and r where a = bq + r, O = r < b.
Step 2 If r = 0, the HCF is b . If r? 0 apply Euclid Lemma to b and r
Step 3 Continue the process until the remainder is zero. The divisor at this stage will be HCF (a, b). Also HCF (a, b) = HCF (b, r)
3. The Fundamental Theorem of Arithmetic: Every composite number can be expressed (factorized) as a product of primes and this factorization is unique, apart from the order in which the prime factors occur.

We hope the NCERT Solutions for Class 10 Maths Chapter 1 Real Numbers Ex 1.1, help you. If you have any query regarding Maths NCERT Solutions Chapter 1 Real Numbers Exercise 1.1, drop a comment below and we will get back to you at the earliest.

Class 10 Maths  Chapter 1 Ex 1.2 (Hindi + English) NCERT Solutions

Ex 1.2 Class 10 Maths Question 1.

Express each number as a product of its prime factors:
(i) 140
(ii) 156
(iii) 3825
(iv) 5005
(v) 7429
Solution: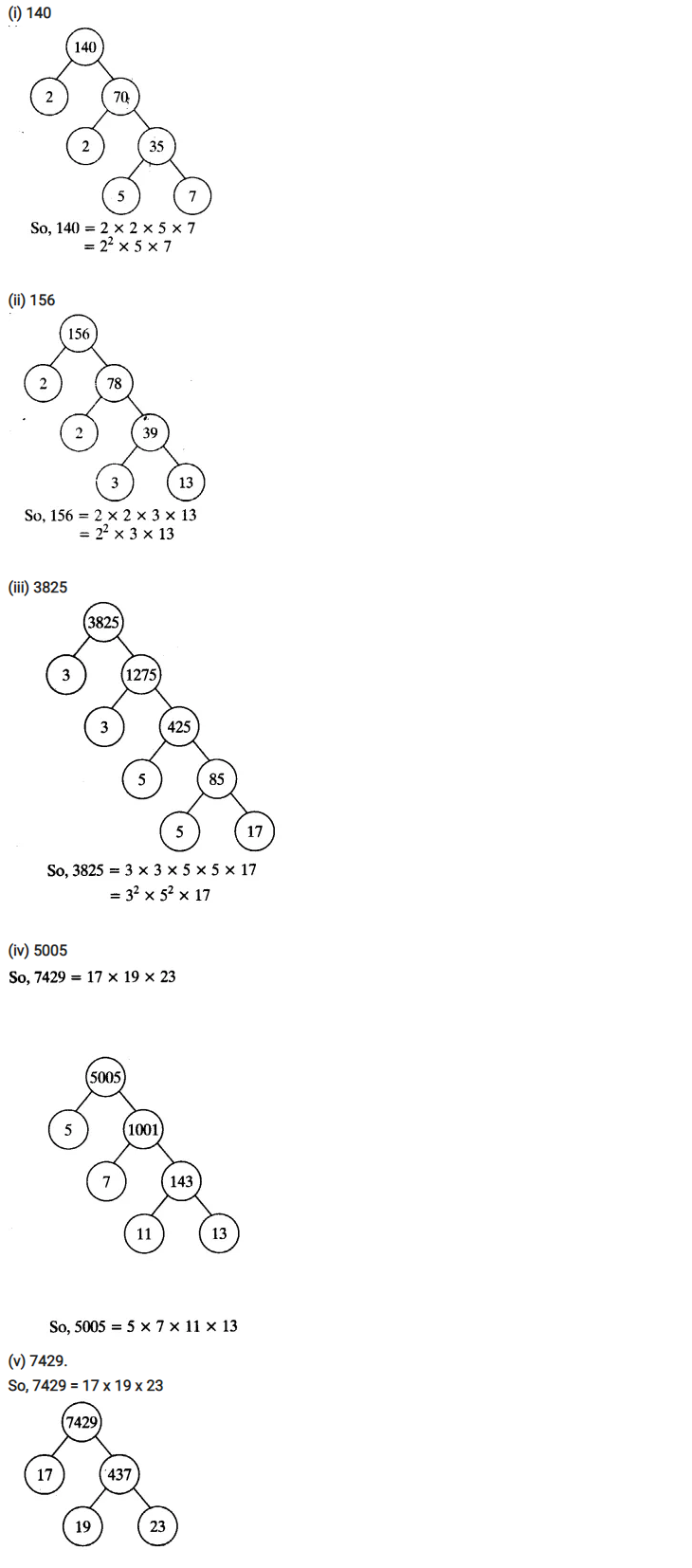

Ex 1.2 Class 10 Maths Question 2.
Find the LCM and HCF of the following pairs of integers and verify that LCM x HCF = Product of the two numbers:
(i) 26 and 91
(ii) 510 and 92
(iii) 336 and 54
Solution:

Ex 1.2 Class 10 Maths Question 3.
Find the LCM and HCF of the following integers by applying the prime factorization method:
(i) 12, 15 and 21
(ii) 17, 23 and 29
(iii) 8, 9 and 25
Solution:

Ex 1.2 Class 10 Maths Question 4:
Given that HCF (306, 657) = 9, find LCM (306, 657).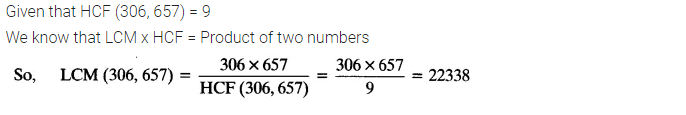

Ex 1.2 Class 10 Maths Question 5.
Check whether 6n can end with the digit 0 for any natural number n.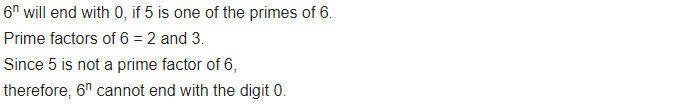

Ex 1.2 Class 10 Maths Question 6.
Explain why 7 x 11 x 13 + 13 and 7 x 6 x 5 x 4 x 3 x 2 x 1 + 5 are composite numbers.

Ex 1.2 Class 10 Maths Question 7.
There is a circular path around a sports field. Sonia takes 18 minutes to drive one round of the field, while Ravi takes 12 minutes for the same. Suppose they both start at the same point and at the same time and go in the same direction. After how many minutes will they meet again at the starting point?
Solution:

NCERT Solutions for Class 10 Maths Chapter 1 Real Numbers (Hindi Medium) Ex 1.2

Class 10 Maths Chapter 1 Real Numbers Ex 1.3 (Hindi + English) NCERT Solutions

Ex 1.3 Class 10 Maths Question 1.

Prove that √5 is irrational.
Solution:

Ex 1.3 Class 10 Maths Question 2.
Show that 3 + √5 is irrational.
Solution:

Ex 1.3 Class 10 Maths Question 3.
Prove that the following are irrational.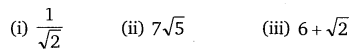

Solution:

NCERT Solutions for Class 10 Maths Chapter 1 Real Numbers (Hindi Medium) Ex 1.3

Class 10 Maths Chapter 1 Real Numbers Ex 1.4 (English + Hindi) NCERT Solutions 

Ex 1.4 Class 10 Maths Question 1.

Without actually performing the long division, state whether the following rational numbers will have a terminating decimal expansion or non-terminating repeating decimal expansion:

Ex 1.4 Class 10 Maths Question 2.
Write down the decimal expansions of those rational numbers in question 1, which have terminating decimal expansions.

Ex 1.4 Class 10 Maths Question 3.
The following real numbers have decimal expansions as given below. In each case, decide whether they are rational or not. If they are rational and of the form pq, what can you say about the prime factors of q?
(i) 43. 123456789
(ii) 0.120120012000120000…
(iii) 43. 123456789¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯

NCERT Solutions for Class 10 Maths Chapter 1 Real Numbers (Hindi Medium) Ex 1.4

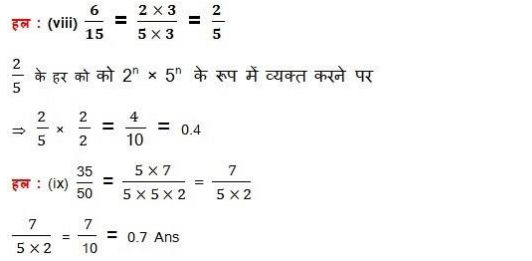
Extra Questions for Class 10 Maths Real Numbers with Answers

Real Numbers Class 10 Extra Questions Very Short Answer Type

Question 1.
After how many places of decimal, the decimal expansion of 4324×53 will terminate?
Answer:
Given 4324×53 is in the lowest form and power of 2 = 4, Power of 5 = 3, Max. {4, 3} = 4
∴ 4324×53 will terminate after 4 places of decimal.

Question 2.
What is the exponent of 3 in the prime factorisation of 864.
Answer: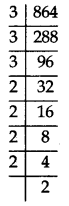

Making prime factors of 864. ,
⇒ 864 = 3 × 3 × 3 × 2 × 2 × 2 × 2 × 2
= 33 × 25
∴ Exponent of 3 in prime factorisation of 864 = 3.

Question 3.
Express 10010 and 140 as prime factors.
Answer:
Prime factors of 10010 = 2 × 5 × 7 × 11 × 13
Prime factors of 140 = 2 × 2 × 5 × 7

Question 4.
What is the H.C.F. of smallest prime number and the smallest composite number ? [CBSE 2018]
Answer:
Smallest prime number = 2 = 21
Smallest composite number = 4 = 22
H.C.F. (2, 4) = 21 = 2

Question 5.
Write a rational number between √5 and √6.
Answer:
∵ √5 = 2.236… and √6 = 2.449…
∴ A rational no between 2.24 and 2.44 (approximately) is 2.3 or 2.31 or 2.32 etc.
Note: Take the lower limit slightly greater than √5 and upper limit slightly lesser than √6 .
⇒ One number between √5 and √6 = 2.3

Question 6.
If p,q are two prime numbers then what is the HCF and LCM of p and q?
Answer:
HCF (p, q) = 1
and LCM(p, q) = pq

Question 7.
A rational number in its decimal expansion is 623.6051. What can you say about the prime factors of q, when this number is expressed in the form pq? Give reasons.
Answer:
Since 623.6051 is a terminating decimal number, so q must be of the form 2m 5n where m, n are natural numbers.

Question 8.
‘Product of two irrational numbers is always an irrational number’. Negate the statement by giving counter example.
Answer:
Take 2 – √5, 2 + √5 both are irrational. Their product
= (2 – √5) (2 + √5)
= 22 – (√5)2 = 4 – 5 = – 1
Which is a rational number.

Question 9.
Can two numbers have 24 as their HCF and 7290 as their LCM? Give reasons.
Answer:
No, because HCF always divide LCM but here 24 does not divide 7290.

Real Numbers Class 10 Extra Questions Short Answer Type-1

Question 1.
Find the HCF of 1260 and 7344 using Euclid’s algorithm.
Or
Show that every positive odd integer is of the form (4q + 1) or (4q + 3), where q is some integer. [CBSE 2019]
Answer:
Taking a = 7344 and b = 12260
Applying Euclid’s Division Algorithm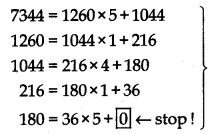

HCF of 1260 and 7344 is 36.
Or
Apply Euclid’s Division Lemma to a and b = 4.
a = 4q + r, 0 ≤ r < 4
⇒ a = 4q, a = 4q + 1, a = 4q + 2 and a = 4q + 3.
Now, a = 4q and a = 4q + 2 are even numbers as both are divisible by 2.
But, 4q + 1 and 4q + 3 are not divisible by 2.
Therefore, when a is odd, it is of the form
a = 4q + 1 or a = 4q + 3 for some integer q.

Question 2.
Show that 3+7√5 that √7 is irrational.
Or
Prove that n2 + n is divisible by 2 for any positive integer n. [CBSE 2019 (C)]
Answer: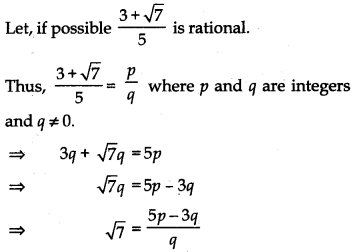

Since, difference of integers is also an integer.
∴ 5p – 3q is an integer.
⇒ 5p−3qq is rational number.
But LHS is √7, which is irrational.
Thus, irrational number = Rational number which is a contradiction.
Thus, our supposition is wrong.
Hence, 3+7√5 is an irrational number.
Or
n2 + n = n(n + 1)
There arise two cases.
Case I: When n is even.
Then (n +1) is odd.
Since, even × odd = even.
∴ Product n(n + 1) is even i.e. divisible by 2.

Case II: When n is odd.
Then (n + 1) is even.
Since, odd × even = even.
∴ n(n + 1) is even i.e. divisible by 2.
So, for any positive integer, (n2 + n) is always divisible by 2.

Question 3.
A positive integer n when divided by 9, gives 7 as remainder. Find the remainder when (3n – 1) is divided by 9.
Answer:
Here n can be written as 9k + 7, where k ∈ N
Now 3n – 1 = 3(9k + 7) – 1 = 27k + 20
Applying Euclid’s division lemma on (27k + 20) and 9, we have
27k + 20 = 9 × (3k + 2) + 2;
where k ∈ N
Thus, 2 is the remainder.

Question 4.
Show that any positive even integer can be written in the form 6q, 6q + 2 or 6q + 4, where q is an integer? [CBSE Delhi 2016]
Answer:
Let take a1 as any positive even integer and
b = 6
Then using Euclid algorithm we get
a = 6q + r
Here r is remainder and value of q is more than or equal to 0 and r = 0, 1, 2, 3, 4, 5 because 0 < r < b and the value of b is 6.
So total possible forms will be 6q + 0, 6q + 2, 6q + 4. 6q + 0
6 is divisible by 2 so, it is an even number. 6q + 2
6 is divisible by 2 and 4 is also divisible by 2.
So, it is an even number.
Hence, any positive even integer can be written in the form 6q, 6q + 2 or 6q + 4 and so on.

Question 5.
In a school, the duration of a period in junior section is 40 minutes and in senior section is 1 hour: If the first bell for each section ring at 9:00 a.m., when will the two bells ring together again? [CBSE 2012 (Sept.)]
Answer:
1 hour = 60 minutes
40 = 2 × 2 × 2 × 5 = 23 × 5
60 = 2 × 2 × 3 × 5 = 22 × 3 × 5
∴ LCM (40, 60) = 23 × 3 × 5 = 120
120 minutes = 2 hours
Hence, the two bells will ring together again at 9:00 + 2:00 = 11:00 a.m.

Question 6.
Explain why (17 × 11 × 2 + 17 × 11 × 5) is a composite number? [CBSE 2012 (Sept.)]
Answer:
17 × 11 × 2 + 17 × 11 × 5
= 17 × 11 × (2 + 5)
= 17 × 11 × 7
Since, 17 × 11 × 2 + 17 × 11 × 5 can be expressed as a product of primes, therefore, it is a composite number.

Real Numbers Class 10 Extra Questions Short Answer Type-2

Question 11.
Use Euclid’s division algorithm to find HCF of 4052 and 12576. [CBSE 2019 (C)]
Answer:
∵ 12576 > 4052, apply the Euclid’s division lemma to 12576 and 4052, to get
12576 = 4052 × 3 + 420
Since 420 ≠ 0, so apply E.D.L. to 4052 and 420 to get
4052 = 420 × 9 + 272
Since, 272 ≠ 0, so apply E.D.L. to 420 and 272
420 = 272 × 1 + 148
Since, 148 ≠ 0, so apply E.D.L. to 272 and 148 to get
272 = 148 × 1 + 124
Since, 124 ≠ 0, so apply E.D.L. to 148 and 124
148 = 124 × 1 + 24
Since, 24 ≠ 0, so apply E.D.L. to 124 and 24
124 = 24 × 5 + 4
Since, 4 ≠ 0, so apply E.D.L. to 24 and 4
24 = 4 × 6 + 0 ← Stop!
Since, remainder has become zero.
∴ HCF (12576, 4052) = 4.

Question 2.
The LCM of two numbers is 14 times their HCF. The sum of LCM and HCF is 600. If one number is 280, then find the other number.
[C.B.S.E Sept 2012]
Answer:
According to the statement of the question, we have:
LCM of two numbers = 14 × HCF of two numbers
Also, LCM + HCF = 600
⇒ 14 × HCF + HCF = 600
⇒ 15 HCF = 600
⇒ HCF = 40
∴ LCM = 14 × 40 = 560
Now, one number is 280
∴ 280 × Other number = 40 × 560
⇒ Other number = 40×560280 = 80

Question 3.
Show that any positive odd integer is of the form 6q + 1, 6q + 3 or 6q + 5, where q is some integer.
Answer:
Apply Euclid’s Division lemma to a and 6, we have
a = 6q + r, where 0 ≤ r ≤ 6
Thus, r can take values 0, 1, 2, 3, 4, 5.
Consider the equation, a = 3q + r
Case 1: When r = 0
Thus, a = 6q
Rewriting the above equation, we have
a = 2(3q)
Which is an even number.

Case 2: When r = 1
Thus, a = 6q + 1
Rewriting the above equation, we have
a = 2 × 3q + 1 – 2m + 1, where m = 3q
Which is an odd number.

Case 3: When r = 2
Thus, a = 6q + 2
Rewriting the above equation, we have
a = 2 × (3q + 1)
= 2m, where m = 3q + 1
Which is an even number.

Case 4: When r = 3
Thus, a = 6q + 3
Rewriting the above equation, we have
a = 2 × (3q + 1) + 1
= 2m + 1, where m = 3q + 1
Which is an odd number.

Case 5: When r = 4
Thus, a = 6q + 4
Rewriting the above equation, we have
a = 2 × (3q + 2)
= 2m + 1, where m = 3q + 2
Which is an even number.

Case 6: When r = 5
Thus, a = 6q + 5
Rewriting the above equation, we have
a = 2 × (3q + 2) + 1
= 2m + 1, where m = 3q + 2
Which is an odd number.
Therefore, any positive odd integer is of the form 6q + 1, 6q + 3 or 6q + 5, where q is some integer.

Question 4.
Using Euclid’s division algorithm, find HCF of 56, 96 and 404.
Answer:
Applying Euclid’s division algorithm to 56 and 96
96 = 56 × 1 + 40
56 = 40 × 1 + 16
40 = 16 × 2 + 8
16 = 8 × 2 + 0
∴ HCF (56, 96) = 8
Next, apply Euclid’s division algorithm to 8 and 404
404 = 8 × 50 + 4
8 = 4 × 2 + 0
Thus, HCF (56, 96, 404) = 4

Question 5.
Find HCF and LCM of 404 and 96 and verify that HCF × LCM = Product of the two given numbers. [CBSE 2018]
Answer:
404 = 2 × 2 × 101 = 22 × 101
96 = 2 × 2 × 2 × 2 × 2 × 3 = 25 × 3
∴ HCF of 404 and 96 = 22 = 4
[Product of smallest power of each common factor]
LCM of 404 and 96 = 101 × 25 × 3 = 9696
[Product of greatest power of each prime factor]
HCF × LCM = 4 × 9696 = 38784
Also 404 × 96 = 38784
Hence HCF × LCM = Product of 404 and 96.

Question 6.
Express 5.4178¯¯¯¯¯¯¯¯ in the pq for,.
Answer:
Let x = 5.4178¯¯¯¯¯¯¯¯
or x = 5.4178178178 ………
∴ 10x = 54.178178178 ………. (1)
Also 1000 (10x) = 54178.178178178 …….
⇒ 10000x = 54178.178178178 ……………. (2)
Subtracting (1) from (2), we have:
10000x – 10x = [54178.178178178…] – [54.178178…]
⇒ 9990x = 54124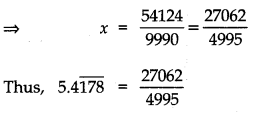

Question 7.
Find the LCM and HCF of 1296 and 5040 by prime factorisation method:
Answer: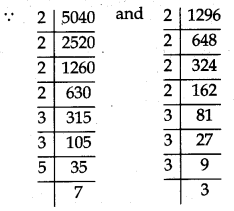

∴ 5040 = 2 × 2 × 2 × 2 × 3 × 3 × 5 × 7
= 24 × 32 × 5 × 7
1296 = 2 × 2 × 2 × 2 × 3 × 3 × 3 × 3
= 24 × 34
∴ LCM = Product of each prime factor with highest powers
= 24 × 34 × 5 × 7
= 16 × 81 × 5 × 7 = 45360
HCF = Product of common prime factors with lowest powers
= 24 × 32
= 16 × 9 = 144

Question 8.
The decimal expansion of the rational number 4324×53, will terminate after how many places of decimal?
Answer: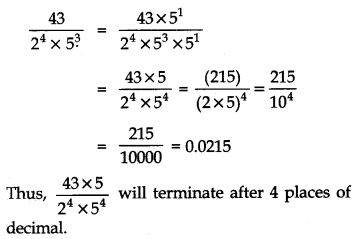

Question 9.
Show that any positive odd integer is of the form 4q + 1 or 4q + 3 where q is a positive integer.
Answer:
Let a be any positive integer and b = 4. Applying Euclid’s division lemma there exist integers q and r such that
a = 4q + r,
where 0 ≤ r < 4
⇒ a – 4q or 4q + 1 or 4q + 2 or 4q + 3
However since ‘a’ is odd we reject the case 4q and 4q + 2 as they both are divisible by 2. Therefore, any positive odd integer is of the form 4q +1 or 4q + 3.

Question 10.
Check whether 14n can end with the digit zero for any natural number n ? [CBSE Delhi 2016]
Answer:
Let, us suppose that 14n ends with the digit 0 for some n ∈ N
∴ 14n is divisible by 5
But, prime factors of 14 are 2 and 7.
∴ Prime factor of (14)n are (2 × 7)n
⇒ It is clear that in prime factorisation of 14″ there is no place for 5.
∴ By Fundamental theorem of Arithmetic
Every composite no. can be expressed as a product of primes and this factorisation is unique, a part from the order in which the prime factor occur.
∴ Our Supposition is wrong.
Hence, there exists no natural number n for which 14n ends with the digit zero.

Question 11.
Prove that √2 is an irrational number. [CBSE 2019]
Answer:
Let, if possible to the contrary that √2 is not irrational number i.e., √2. is a rational number.
That mean √2 can be expressed in pq form where
p and q are coprime positive integers and q ≠ 0.
So, √2 = pq
⇒ p2 = 2q2
Thus, p2 is a multiple of 2
⇒ p is a multiple of 2.
Let p = 2m for some integer m.
⇒ q2 = 2m2.
Thus, q2 is a multiple of 2.
⇒ q is a multiple of 2.
Hence, 2 is a common factor of p and q.
This contradicts the fact that p and q are coprimes.
∴ Our supposition is wrong.
Hence, √2 is an irrational number.

Real Numbers Class 10 Extra Questions Long Answer Type 1

Question 1.
A, B and C starts cycling around a circular path in the same direction at the same time. Circumference of the path is 1980 m. If speed of A is 330 m/min, speed of B is 198 n0nin and that of C is 220 n^min and they start from the same point, then after what time will they be together at the starting point?
Answer:
As =  Distance  Speed 
Time taken by A to complete one round
= 1980330 = 6 min
Time taken by B to complete one round
= 1980198 = 10 min
Time taken by C to complete one round
= 1980220 = 9 min
The three cyclists will be together after LCM (6, 10, 9)
6 = 2 × 3
10 = 2 × 5
9 = 32
LCM (6, 10, 9) = 21 × 32 × 5 = 90 min.

Question 2.
The HCF of 408 and 1032 is expressible in the form 1032 m – 2040. Find the value of m. Also, find the LCM of 408 and 1032.
Answer:
Let us find HCF of 408 and 1032.
Here, 1032 > 408
∴ 1032 = 2 × 408 + 216
408 = 1 × 216 + 192
216 = 1 × 192 + 24
192 = 8 × 24 + 0
Thus, HCF of 408 and 1032 is 24.
Now, HCF (408, 1032)
i.e., 24 = 1032 × m – 2040
⇒ 1032 × m = 24 + 2040
⇒ 1032 × m = 2064
⇒ m = 20641032 = 2
408 = 23 × 3 × 17
1032 = 23 × 3 × 43 ,
∴ LCM of 408 and 1032 = 23 × 3 × 17 × 43 = 17544.

Question 3.
Obtain the HCF of420 and 272 by using Euclid’s division algorithm and verify the same by using Fundamental theorem of Arithmetic. ‘
Answer:
Case I: Using Euclid’s division algorithm
420 = 272 × 1 + 148
272 = 148 × 1 + 124,
148 = 124 × 1 + 24
124 = 24 × 5 + 4 24 = 4×6 + 0
∴ HCF (420,272) = 4

Case II: Using Fundamental theorem of Arithmetic.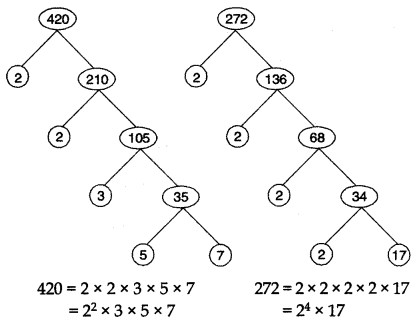

∴ HCF (420, 272) = 22 = 4
rom I and II the result obtained is verified.

Question 4.
If ‘h’ is HCF of 609 and 957. Find x and y satisfying h = 609x + 957y. Also show that x and y are not unique.
Answer:
Here 957 > 609
So, starting with
a = 957 and b = 609 and applying Euclid’s division algorithm,
we get
957 = 6 × 1 + 348 …………… (i)
609 = 348 × 1 + 261 …………… (ii)
348 = 261 × 1 + 87 …………… (iii)
261 = 87 × 3 + 0 ← remainder (r) …………… (iv)
⇒ HCF (609, 957) = 87
Alternatively,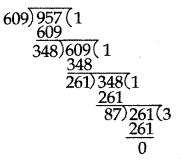

From (iii)
⇒ 87 = 348 – 261 × 1,
= 348 – (609 – 348 × 1) × 1
[∵ From (ii) 261 = 609 – 348 × 1]
= 348 – 609 × 1 + 348 × 1
= 348 × 2 – 609 × 1
= (957 – 609 × 1) × 2 – 609 × 1
= 957 × 2 – 609 × 2 – 609 × 1
= 957 × (2) + 609 (- 2 -1)
= 957 × (2) + 609 × (-3) …….. (iv)
Thus, 87 = 957y + 609x where y = 2 and x = – 3
Adding and subtracting 957 × 609 in (iv),
we get
87 = 957 × 2 + 609 × (- 3) + 957 × 609 – 957 × 609
= 957 × 2 + 957 × 609 + 609 × (-3) + 609 × (-957)
= 957 × (2 + 609) + 609 × (- 3 – 957)
⇒ 87 = 957 × (611) + 609 × (- 960) ………….. (v)
= 957x + 609y
Where x = 611, y = – 960
(v) represents another linear combination and hence x and y are not unique.

Real Numbers Class 10 Extra Questions HOTS

Question 1.
Find the greatest number that will divide 43,91 and 183 so as to leave the same remainder in each case.
Answer:
Here we look at the difference between the given numbers. Let the remainder in each case be x. then, 43 – x, 91 – x and 183 – x are divisible by the required number.
⇒ (91 – x) – (43 – x), (183 – x) – (91 – x) and (183 – x) – (43 – x) are divisible by the required number.
i.e., (91 – 43), (183 – 91) and (183 – 43) are divisible by the required number.
Required number
= HCF of (91 – 43), (183 – 91) and (183 – 43)
= HCF (48, 92,140)
As 48 = 24 × 3,92 = 23 × 22,
140 = 22 × 5 × 7
∴ HCF = 22 = 4
Thus, 4 is the greatest number that divides 43,91 and 183 leaving same remainder.

Question 2.
Coloured pencils are available in market in packs of 12 each and crayons in pack of 32 each. A girl wants full pack of both and the same number of pencils and crayons, how many of each would she need to buy ?
Answer:
LCM (12,32) = 96
∴ No. of packets of coloured pencils
=  LCM  Qty. in one packed  = 9612 = 8
No. of packets of crayon = 9632 = 3.

Question 3.
The set of Mathematics, Physics and Physical Education books have to be stacked in such a way that all the books are stored topic wise. The number of Mathematics, Physics and Physical Education books are 14, 18 and 22. Determine the number of stacks of each books provided books are of the same thickness.
Answer:
Firstly, to arrange the books as according to condition, find HCF of 14, 18 and 22.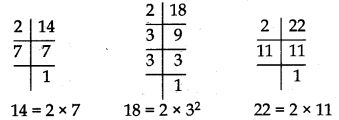

HCF (14, 18, 22) = 2
⇒ There are only 2 books in each stack.
Now, number of stacks of Mathematics books = 142 = 7
Number of stacks of Physics books = 182 = 9.
Number of stacks of Physical Education books = 222 = 11

Question 4.
Prove that there is no rational number whose square is 6.
Answer:
Let ab be a rational number whose square is 6.
Then 6 = (ab)2, where a and b are prime to each other and b > 0.
⇒ 6b2 = a2
⇒ 3(2b2) = a2
Thus, a2 is divisible by 3, and so a is divisible by 3.
Let a = 3p, where p is some integer.
Then, a2 = 6b2 gives
(3p)2 = 6b2
⇒ 9 p2 = 6b2
⇒ 3 p2 = 2b2
This shows that 2 b2 is divisible by 3, so b2 is divisible by 3, and thus b is divisible by 3. Thus, both a and b are divisible by 3 which is a contradiction.
Hence, there is no rational number whose square is 6.

Question 5.
If p and q are two odd prime numbers, show that p2 – g2 is composite.
Answer:
Let p = 2m + 1, q = 2n + 1, where m and n are natural numbers.
Now, (p2 – q2) = (p – q)(p + q) ,
But, p- q = (2m + 1) – (2n + 1) = 2(m – n)
p + q = (2m + 1) + (2n + 1) = 2 (m + n + 1)
Clearly both factors of (p2 – q2) are even i.e., none of the divisors (p – q) and (p + q) is equal to 1.
⇒ (p2 – q2) is a composite number.

Multiple Choice Questions

Choose the correct option out of four given in each of the following:

Question 1.
The value of H.C.F × L.C.M. for the number 183 and 30 is:
(a) 5490
(b) 610
(c) 61
(d) 549
Answer:
(a) 5490

Question 2.
Which of the following is not true about 511500?
(a) It has a terminating decimal expansion
(b) It has a non-terminating decimal expansion
(c) It is a rational number which terminates after 5 places of decimal
(d) Its denominator, in lowest form, has prime factorisation of the form 2m × 5n.
Answer:
(c) It is a rational number which terminates after 5 places of decimal

Question 3.
The decimal expansion of 24627×5−3 terminates after
(a) 7 places of decimals
(b) 10 places of decimals
(c) 6 places of decimals
(d) Can’t be determined.
Answer:
(c) 6 places of decimals

Question 4.
The decimal expansion of
π =  Circumference of the circle  diameter of circle  is always
(a) terminating
(b) non-terminating, non repeating
(c) terminating repeating
(d) non terminating repeating.
Answer:
(b) non-terminating, non repeating

Question 5.
The least number divisible by 2,3,7 and 9 is:
(a) 126
(b) 256
(c) 251
(d) 189
Answer:
(a) 126

Question 6.
Let p/q be a rational number. Then, the condition on q such that p/q has a non terminating but repeating decimal expansion is
(a) q = 2m × 5n; m, n are whole numbers
(b) q ≠ 2m × 5n; m, n are whole numbers
(c) q = 2m × 3n; m, n are whole numbers
(d) q ≠ 2m × 3n; m, n are whole numbers
Answer:
(b) q ≠ 2m × 5n; m, n are whole numbers

Question 7.
The decimal representation of an irrational number is always .
(a) terminating
(b) terminating, repeating
(c) non-terminating, repeating
(d) non-terminating, non repeating.
Answer:
(d) non-terminating, non repeating.

Question 8.
The H.C.F and L.C.M. of two numbers are 4 and 48. If one number is 12, then the other number is:
(a) 8
(b) 24
(c) 4
(d) 16
Answer:
(d) 16

Question 9.
According to Fundamental Theorem of Arithmetic, if p (a prime number) divides a2, and a is non-negative integer then:
(a) a divides p
(b) p divides a
(c) a2 divides p
(d) p2 divides a
Answer:
(b) p divides a

Question 10.
If the product of two coprime numbers is 217, then their L.C.M. is
(a) Can’t be determined
(b) 217
(c) 651
(d) 434
Answer:
(b) 217

Question 11.
Euclid’s division lemma states that for any two positive integers a and b there exist unique integers q and r such that a = bq + r, where r must satisfy
(a) 1 < r < b
(b) 0 < r ≤ b
(c) 0 ≤ r < b
(d) 0 < r < b
Answer:
(c) 0 ≤ r < b

Question 12.
For some integer p, every odd integer is of the form
(a) p
(b) p + 1
(c) 2p
(d) 2p + 1
Answer:
(d) 2p + 1

Question 13.
Which of the following is false:
(a) H.C.F. (a,b) × L.C.M.(a ,b) = a × b
(b) L.C.M. (p, q, r) = p × q × r; if p, q, r are prime numbers
(c) H.C.F. (p, q, r) = 1, if p, q, r are prime numbers
(d) H.C.F. (p, q, r) × L.C.M.(p, q, r) = p × q × r
Answer:
(d) H.C.F. (p, q, r) × L.C.M.(p, q, r) = p × q × r

Question 14.
Two integers p and q are expressed in powers of primes as p = a15b3ef7 and q = a4bgc2 where a, b, c, d, e, f, g are primes. Then H.C.F. (p, q) is:
(a) a4bg
(b) a4b
(c) a15b3ef7c2
(d) a4bc2
Answer:
(b) a4b

Question 15.
The product of two consecutive natural numbers is always:
(a) an odd number
(b) an even number
(c) a prime number
(d) a composite number
Answer:
(b) an even number

Fill in the blanks:

Question 1.
If a number can’t be expressed in the form p/q, where p and q are integers and q ≠ 0, then it is known as ____________ number.
Answer:
Irrational

Question 2.
If a rational number p/q, where q ≠ 0 and p, q are coprimes, has a terminating decimal expansion then q has prime factors ___________ and ____________ .
Answer:
2 and 5

Question 3.
If a rational number piq (in lowest form) has a non-terminating and repeating decimal expansion, then prime factorisation of q is of the form ______________ .
Answer:
2m × 5n, where m, n are non-negative integers

Question 4.
Euclid’s division algorithm is a technique to compute the ______________ of two given positive integers.
Answer:
H.C.F

Question 5.
H.C.F. of two or more prime numbers is always
Answer:
1

Question 6.
7 × 11 × 13+ 3 is a ____________ number, (prime/composite/irrational)
Answer:
Composite

Question 7.
If product of two coprimes is 765, then their L.C.M. = ____________.
Answer:
765

Question 8.
Sum of a rational and irrational number is always ____________ number.
Answer:
irrational

Question 9.
Product of any irrational number with a rational number ‘x’ is always rational. Then, x is ____________.
Answer:
0

Question 10.
Any number ending with ‘0’ must have ______________ and ______________ as its prime factors.
Answer:
2, 5

You can also download NCERT Solutions For Class 10 Maths to help you to revise the complete syllabus and score more marks in your examinations.

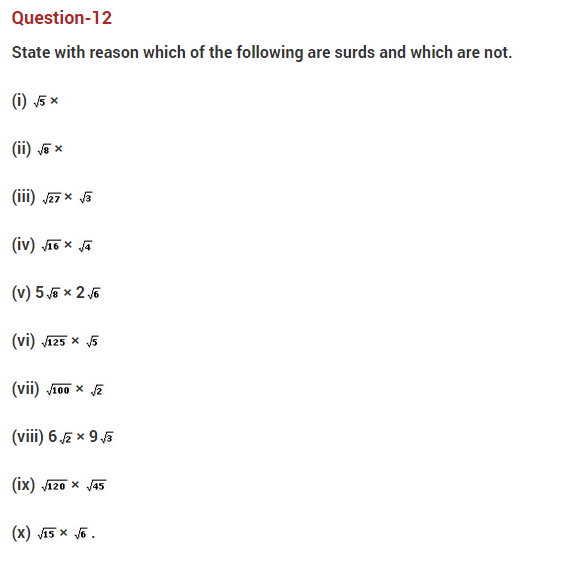
Important Questions for Class 10 Maths Chapter 1 Real Numbers

Real Numbers Class 10 Important Questions Very Short Answer (1 Mark)

Question 1.
The decimal expansion of the rational number 432453 will terminate after how many places of decimals? (2013)
Solution: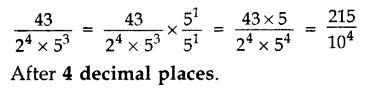

Question 2.
Write the decimal form of 129275775
Solution:
Non-terminating non-repeating.

Question 3.
Find the largest number that will divide 398, 436 and 542 leaving remainders 7, 11, and 15 respectively.
Solution:
Algorithm
398 – 7 = 391, 436 – 11 = 425, 542 – 15 = 527
HCF of 391, 425, 527 = 17

Question 4.

Express 98 as a product of its primes.
Solution:
2 × 72

Question 5.
If the HCF of 408 and 1032 is expressible in the form 1032 × 2 + 408 × p, then find the value of p.
Solution:
HCF of 408 and 1032 is 24.
1032 × 2 + 408 × (p) = 24
408p = 24 – 2064
p = -5

Real Numbers Class 10 Important Questions Short Answer-I (2 Marks)

Question 6.
HCF and LCM of two numbers is 9 and 459 respectively. If one of the numbers is 27, find the other number. (2012)
Solution:
We know,
1st number × 2nd number = HCF × LCM
⇒ 27 × 2nd number = 9 × 459
⇒ 2nd number = 9×45927 = 153

Question 7.
Find HCF and LCM of 13 and 17 by prime factorisation method. (2013)
Solution:
13 = 1 × 13; 17 = 1 × 17
HCF = 1 and LCM = 13 × 17 = 221

Question 8.
Find LCM of numbers whose prime factorisation are expressible as 3 × 52 and 32 × 72. (2014)
Solution:
LCM (3 × 52, 32 × 72) = 32 × 52 × 72 = 9 × 25 × 49 = 11025

Question 9.
Find the LCM of 96 and 360 by using fundamental theorem of arithmetic. (2012)
Solution:
96 = 25 × 3
360 = 23 × 32 × 5
LCM = 25 × 32 × 5 = 32 × 9 × 5 = 1440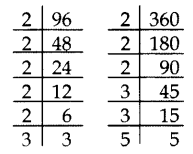

Question 10.
Find the HCF (865, 255) using Euclid’s division lemma. (2013)
Solution:
865 > 255
865 = 255 × 3 + 100
255 = 100 × 2 + 55
100 = 55 × 1 + 45
55 = 45 × 1 + 10
45 = 10 × 4 + 5
10 = 5 × 2 + 0
The remainder is 0.
HCF = 5

Question 11.
Find the largest number which divides 70 and 125 leaving remainder 5 and 8 respectively. (2015)
Solution:
It is given that on dividing 70 by the required number, there is a remainder 5.
This means that 70 – 5 = 65 is exactly divisible by the required number.
Similarly, 125 – 8 = 117 is also exactly divisible by the required number.
65 = 5 × 13
117 = 32 × 13
HCF = 13
Required number = 13

Question 12.
Find the prime factorisation of the denominator of rational number expressed as 6.12¯ in simplest form. (2014)
Solution:
Let x = 6.12¯ …(i)
100x = 612.12¯ …(ii)
…[Multiplying both sides by 100]
Subtracting (i) from (ii),
99x = 606
x = 60699 = 20233
Denominator = 33
Prime factorisation = 3 × 11

Question 13.
Complete the following factor tree and find the composite number x. (2014)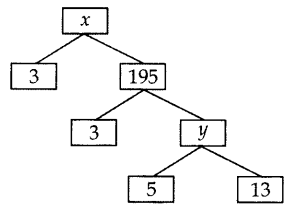

Solution:
y = 5 × 13 = 65
x = 3 × 195 = 585

Question 14.
Prove that 2 + 3√5 is an irrational number. (2014)
Solution:
Let us assume, to the contrary, that 2 + 3√5 is rational.
So that we can find integers a and b (b ≠ 0).
Such that 2 + 3√5 = ab, where a and b are coprime.
Rearranging the above equation, we get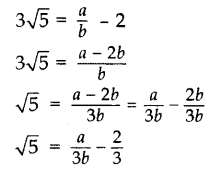

Since a and b are integers, we get a3b−23 is rational and so √5 is rational.
But this contradicts the fact that √5 is irrational.
So, we conclude that 2 + 3√5 is irrational.

Question 15.
Show that 3√7 is an irrational number. (2016)
Solution:
Let us assume, to the contrary, that 3√7 is rational.
That is, we can find coprime a and b (b ≠ 0) such that 3√7 = ab
Rearranging, we get √7 = a3b
Since 3, a and b are integers, a3b is rational, and so √7 is rational.
But this contradicts the fact that √7 is irrational.
So, we conclude that 3√7 is irrational.

Question 16.
Explain why (17 × 5 × 11 × 3 × 2 + 2 × 11) is a composite number? (2015)
Solution:
17 × 5 × 11 × 3 × 2 + 2 × 11 …(i)
= 2 × 11 × (17 × 5 × 3 + 1)
= 2 × 11 × (255 + 1)
= 2 × 11 × 256
Number (i) is divisible by 2, 11 and 256, it has more than 2 prime factors.
Therefore (17 × 5 × 11 × 3 × 2 + 2 × 11) is a composite number.

Question 17.
Check whether 4n can end with the digit 0 for any natural number n. (2015)
Solution:
4n = (22)n = 22n
The only prime in the factorization of 4n is 2.
There is no other prime in the factorization of 4n = 22n
(By uniqueness of the Fundamental Theorem of Arithmetic).
5 does not occur in the prime factorization of 4n for any n.
Therefore, 4n does not end with the digit zero for any natural number n.

Question 18.
Can two numbers have 15 as their HCF and 175 as their LCM? Give reasons. (2017 OD)
Solution:
No, LCM = Product of the highest power of each factor involved in the numbers.
HCF = Product of the smallest power of each common factor.
We can conclude that LCM is always a multiple of HCF, i.e., LCM = k × HCF
We are given that,
LCM = 175 and HCF = 15
175 = k × 15
⇒ 11.67 = k
But in this case, LCM ≠ k × HCF
Therefore, two numbers cannot have LCM as 175 and HCF as 15.

Real Numbers Class 10 Important Questions Short Answer-II (3 Marks)

Question 19.
Prove that √5 is irrational and hence show that 3 + √5 is also irrational. (2012)
Solution:
Let us assume, to the contrary, that √5 is rational.
So, we can find integers p and q (q ≠ 0), such that
√5 = pq, where p and q are coprime.
Squaring both sides, we get
5 = p2q2
⇒ 5q2 = p2 …(i)
⇒ 5 divides p2
5 divides p
So, let p = 5r
Putting the value of p in (i), we get
5q2 = (5r)2
⇒ 5q2 = 25r2
⇒ q2 = 5r2
⇒ 5 divides q2
5 divides q
So, p and q have atleast 5 as a common factor.
But this contradicts the fact that p and q have no common factor.
So, our assumption is wrong, is irrational.
√5 is irrational, 3 is a rational number.
So, we conclude that 3 + √5 is irrational.

Question 20.
Prove that 3 + 2√3 is an irrational number. (2014)
Solution:
Let us assume to the contrary, that 3 + 2√3 is rational.
So that we can find integers a and b (b ≠ 0).
Such that 3 + 2√3 = ab, where a and b are coprime.
Rearranging the equations, we get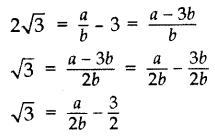

Since a and b are integers, we get a2b−32 is rational and so √3 is rational.
But this contradicts the fact that √3 is irrational.
So we conclude that 3 + 2√3 is irrational.

Question 21.
Three bells toll at intervals of 9, 12, 15 minutes respectively. If they start tolling together, after what time will they next toll together? (2013)
Solution:
9 = 32, 12 = 22 × 3, 15 = 3 × 5
LCM = 22 × 32 × 5 = 4 × 9 × 5 = 180 minutes or 3 hours
They will next toll together after 3 hours.

Question 22.
Two tankers contain 850 liters and 680 liters of petrol. Find the maximum capacity of a container which can measure the petrol of each tanker in the exact number of times. (2012)
Solution:
To find the maximum capacity of a container which can measure the petrol of each tanker in the exact number of times, we find the HCF of 850 and 680.
850 = 2 × 52 × 17
680 = 23 × 5 × 17
HCF = 2 × 5 × 17 = 170
Maximum capacity of the container = 170 liters.

Question 23.
The length, breadth, and height of a room are 8 m 50 cm, 6 m 25 cm and 4 m 75 cm respectively. Find the length of the longest rod that can measure the dimensions of the room exactly. (2015)
Solution:
To find the length of the longest rod that can measure the dimensions of the room exactly, we have to find HCF.
L, Length = 8 m 50 cm = 850 cm = 21 × 52 × 17
B, Breadth = 6 m 25 cm = 625 cm = 54
H, Height = 4 m 75 cm = 475 cm = 52 × 19
HCF of L, B and H is 52 = 25 cm
Length of the longest rod = 25 cm

Question 24.
Three alarm clocks ring at intervals of 4, 12 and 20 minutes respectively. If they start ringing together, after how much time will they next ring together? (2015)
Solution:
To find the time when the clocks will next ring together,
we have to find LCM of 4, 12 and 20 minutes.
4 = 22
12 = 22 × 3
20 = 22 × 5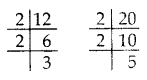

LCM of 4, 12 and 20 = 22 × 3 × 5 = 60 minutes.
So, the clocks will ring together again after 60 minutes or one hour.

Question 25.
In a school, there are two Sections A and B of class X. There are 48 students in Section A and 60 students in Section B. Determine the least number of books required for the library of the school so that the books can be distributed equally among all students of each Section. (2017 OD)
Solution:
Since the books are to be distributed equally among the students of Section A and Section B. therefore, the number of books must be a multiple of 48 as well as 60.
Hence, required num¬ber of books is the LCM of 48 and 60.
48 = 24 × 3
60 = 22 × 3 × 5
LCM = 24 × 3 × 5 = 16 × 15 = 240
Hence, required number of books is 240.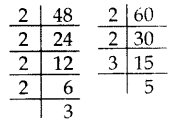

Question 26.
By using Euclid’s algorithm, find the largest number which divides 650 and 1170. (2017 OD)
Solution:
Given numbers are 650 and 1170.
1170 > 650
1170 = 650 × 1 + 520
650 = 520 × 1 + 130
520 = 130 × 4 + 0
HCF = 130
The required largest number is 130.

Question 27.
Find the HCF of 255 and 867 by Euclid’s division algorithm. (2014)
Solution:
867 is greater than 255. We apply the division lemma to 867 and 255, to get
867 = 255 × 3 + 102
We continue the process till the remainder is zero
255 = 102 × 2 + 51
102 = 51 × 2 + 0, the remainder is zero.
HCF = 51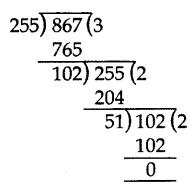

Question 28.
Using Euclid’s division algorithm, find whether the pair of numbers 847, 2160 are coprime or not.
To find out the minimum (least) time when the bells toll together next, we find the LCM of 9, 12, 15.
Solution:

Real Numbers Class 10 Important Questions Long Answer (4 Marks)

Question 29.
Prove that 3 + 2√5 is irrational. (2012, 2017 D)
Solution:
Let us assume, to the contrary, that 3 + 2√5 is rational
So that we can find integers a and b (b ≠ 0), such that
3 + 2 √5 = ab, where a and b are coprime.
Rearranging this equation, we get

Since a and b are integers, we get that a2b – 32 is rational and so √5 is rational.
But this contradicts the fact that √5 is irrational.
So we conclude that 3 + 2√5 is irrational.

Question 30.
There are 104 students in class X and 96 students in class IX in a school. In a house examination, the students are to be evenly seated in parallel rows such that no two adjacent rows are of the same class. (2013)
(a) Find the maximum number of parallel rows of each class for the seating arrange¬ment.
(b) Also, find the number of students of class IX and also of class X in a row.
(c) What is the objective of the school administration behind such an arrangement?
Solution:
104 = 23 × 13
96 = 25 × 3
HCF = 23 = 8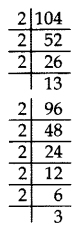

(a) Number of rows of students of class X = 1048 = 13
Number maximum of rows class IX = 968 = 12
Total number of rows = 13 + 12 = 25
(b) No. of students of class IX in a row = 8
No. of students of class X in a row = 8
(c) The objective of school administration behind such an arrangement is fair and clean examination, so that no student can take help from any other student of his/her class.

Question 31.
Dudhnath has two vessels containing 720 ml and 405 ml of milk respectively. Milk from these containers is poured into glasses of equal capacity to their brim. Find the minimum number of glasses that can be filled. (2014)
Solution:
1st vessel = 720 ml; 2nd vessel = 405 ml
We find the HCF of 720 and 405 to find the maximum quantity of milk to be filled in one glass.
405 = 34 × 5
720 = 24 × 32 × 5
HCF = 32 × 5 = 45 ml = Capacity of glass
No. of glasses filled from 1st vessel = 72045 = 16
No. of glasses filled from 2nd vessel = 40545 = 9
Total number of glasses = 25

Question 32.
Amita, Sneha, and Raghav start preparing cards for all persons of an old age home. In order to complete one card, they take 10, 16 and 20 minutes respectively. If all of them started together, after what time will they start preparing a new card together? (2013)
Solution:
To find the earliest (least) time, they will start preparing a new card together, we find the LCM of 10, 16 and 20.
10 = 2 × 5
16 = 24
20 = 22 × 5
LCM = 24 × 5 = 16 × 5 = 80 minutes
They will start preparing a new card together after 80 minutes.

Question 33.
Find HCF of numbers 134791, 6341 and 6339 by Euclid’s division algorithm. (2015)
Solution:
First, we find HCF of 6339 and 6341 by Euclid’s division method.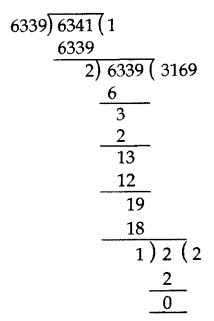

6341 > 6339
6341 = 6339 × 1 + 2
6339 = 2 × 3169 + 1
2 = 1 × 2 + 0
HCF of 6341 and 6339 is 1.
Now, we find the HCF of 134791 and 1
134791 = 1 × 134791 + 0
HCF of 134791 and 1 is 1.
Hence, the HCF of the given three numbers is 1.

Question 34.
If two positive integers x and y are expressible in terms of primes as x = p2q3 and y = p3q, what can you say about their LCM and HCF. Is LCM a multiple of HCF? Explain. (2014)
Solution:
x = p2q3 and y = p3q
LCM = p3q3
HCF = p2q …..(i)
Now, LCM = p3q3
⇒ LCM = pq2 (p2q)
⇒ LCM = pq2 (HCF)
Yes, LCM is a multiple of HCF.
Explanation:
Let a = 12 = 22 × 3
b = 18 = 2 × 32
HCF = 2 × 3 = 6 …(ii)
LCM = 22 × 32 = 36
LCM = 6 × 6
LCM = 6 (HCF) …[From (ii)]
Here LCM is 6 times HCF.

Question 35.
Show that one and only one out of n, (n + 1) and (n + 2) is divisible by 3, where n is any positive integer. (2015)
Solution:
Let n, n + 1, n + 2 be three consecutive positive integers.
We know that n is of the form 3q, 3q + 1, or 3q + 2.
Case I. When n = 3q,
In this case, n is divisible by 3,
but n + 1 and n + 2 are not divisible by 3.
Case II. When n = 3q + 1,
In this case n + 2 = (3q + 1) + 2
= 3q + 3
= 3(q + 1 ), (n + 2) is divisible by 3,
but n and n + 1 are not divisible by 3.
Case III.
When n = 3q + 2, in this case,
n + 1 = (3q + 2) + 1
= 3q + 3 = 3 (q + 1 ), (n + 1) is divisible by 3,
but n and n + 2 are not divisible by 3.
Hence, one and only one out of n, n + 1 and n + 2 is divisible by 3.

Question 36.
Find the HCF and LCM of 306 and 657 and verify that LCM × HCF = Product of the two numbers. (2016 D)
Solution:
306 = 2 × 32 × 17
657 = 32 × 73
HCF = 32 = 9
LCM = 2 × 32 × 17 × 73 = 22338
L.H.S. = LCM × HCF = 22338 × 9 = 201042
R.H.S. = Product of two numbers = 306 × 657 = 201042
L.H.S. = R.H.S.

Question 37.
Show that any positive odd integer is of the form 41 + 1 or 4q + 3 where q is a positive integer. (2016 OD)
Solution:
Let a be a positive odd integer
By Euclid’s Division algorithm:
a = 4q + r …[where q, r are positive integers and 0 ≤ r < 4]
a = 4q
or 4q + 1
or 4q + 2
or 4q + 3
But 4q and 4q + 2 are both even
a is of the form 4q + 1 or 4q + 3.

Class 10 Maths Notes Chapter 1 Real Numbers

R = Real Numbers:
All rational and irrational numbers are called real numbers.

I = Integers:
All numbers from (…-3, -2, -1, 0, 1, 2, 3…) are called integers.

Q = Rational Numbers:
Real numbers of the form pq, q ≠ 0, p, q ∈ I are rational numbers.

• All integers can be expressed as rational, for example, 5 = 51
• Decimal expansion of rational numbers terminating or non-terminating recurring.

Q’ = Irrational Numbers:
Real numbers which cannot be expressed in the form pq and whose decimal expansions are non-terminating and non-recurring.

• Roots of primes like √2, √3, √5 etc. are irrational

N = Natural Numbers:
Counting numbers are called natural numbers. N = {1, 2, 3, …}

W = Whole Numbers:
Zero along with all natural numbers are together called whole numbers. {0, 1, 2, 3,…}

Even Numbers:
Natural numbers of the form 2n are called even numbers. (2, 4, 6, …}

Odd Numbers:
Natural numbers of the form 2n -1 are called odd numbers. {1, 3, 5, …}

• Why can’t we write the form as 2n+1?

Remember this!

• All Natural Numbers are whole numbers.
• All Whole Numbers are Integers.
• All Integers are Rational Numbers.
• All Rational Numbers are Real Numbers.

Prime Numbers:
The natural numbers greater than 1 which are divisible by 1 and the number itself are called prime numbers, Prime numbers have two factors i.e., 1 and the number itself For example, 2, 3, 5, 7 & 11 etc.

• 1 is not a prime number as it has only one factor.

Composite Numbers:
The natural numbers which are divisible by 1, itself and any other number or numbers are called composite numbers. For example, 4, 6, 8, 9, 10 etc.
Note: 1 is neither prime nor a composite number.

I. Euclid’s Division lemma
Given two positive integers a and b, there exist unique integers q and r satisfying a = bq + r, 0 ≤ r ≤ b.
Notice this. Each time ‘r’ is less than b. Each ‘q’ and ‘r’ is unique.

II. Application of lemma
Euclid’s Division lemma is used to find HCF of two positive integers. Example: Find HCF of 56 and 72 ?
Steps:

• Apply lemma to 56 and 72.
• Take bigger number and locate ‘b’ and ‘r’. 72 = 56 × 1 + 16
• Since 16 ≠ 0, consider 56 as the new dividend and 16 as the new divisor. 56 = 16 × 3 + 8
• Again, 8 ≠ 0, consider 16 as new dividend and 8 as new divisor. 16 = 8 × 2 + 0

Since remainder is zero, divisor (8) is HCF.
Although Euclid’s Division lemma is stated for only positive integers, it can be extended for all integers except zero, i.e., b ≠ 0.

III. Constructing a factor tree
Steps

• Write the number as a product of prime number and a composite number
  Example:
  Factorize 48
• Repeat the process till all the primes are obtained
  ∴ Prime factorization of 48 = 24 x 3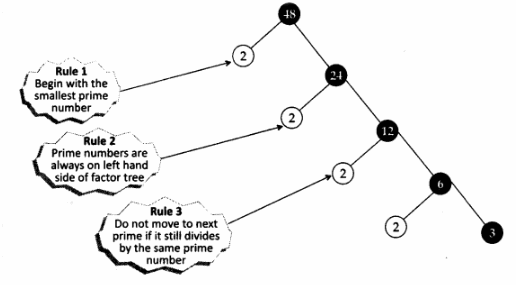
  

IV. Fundamental theorem of Arithmetic
Every composite number can be expressed as a product of primes, and this expression is unique, apart from the order in which they appear.
Applications:

1. To locate HCF and LCM of two or more positive integers.
2. To prove irrationality of numbers.
3. To determine the nature of the decimal expansion of rational numbers.

1. Algorithm to locate HCF and LCM of two or more positive integers:

Step I:
Factorize each of the given positive integers and express them as a product of powers of primes in ascending order of magnitude of primes.
Step II:
To find HCF, identify common prime factor and find the least powers and multiply them to get HCF.
Step III:
To find LCM, find the greatest exponent and then multiply them to get the LCM.

2. To prove Irrationality of numbers:

• The sum or difference of a rational and an irrational number is irrational.
• The product or quotient of a non-zero rational number and an irrational number is irrational.

3. To determine the nature of the decimal expansion of rational numbers:

• Let x = p/q, p and q are co-primes, be a rational number whose decimal expansion terminates. Then the prime factorization of’q’ is of the form 2m5n, m and n are non-negative integers.
• Let x = p/q be a rational number such that the prime factorization of ‘q’ is not of the form 2m5n, ‘m’ and ‘n’ being non-negative integers, then x has a non-terminating repeating decimal expansion.

Alert!

• 23 can be written as: 23 = 2350
• 52 can be written as: 52 = 2052

Here Is The Class 10 Maths All NCERT Solutions In Hindi + English With Extra Questions, Notes And Important Questions

• Chapter 1 Real Numbers
• Chapter 2 Polynomials
• Chapter 3 Pair of Linear Equations in Two Variables
• Chapter 4 Quadratic Equations
• Chapter 5 Arithmetic Progressions
• Chapter 6 Triangles
• Chapter 7 Coordinate Geometry
• Chapter 8 Introduction to Trigonometry
• Chapter 9 Applications of Trigonometry
• Chapter 10 Circle
• Chapter 11 Constructions
• Chapter 12 Areas related to Circles
• Chapter 13 Surface Areas and Volumes
• Chapter 14 Statistics
• Chapter 15 Probability