Class 10 Maths Chapter 8 Introduction to Trigonometry Ex 8.1 (English + Hindi) NCERT Solutions

Class 10 Maths Chapter 8 Introduction to Trigonometry Ex 8.1 (English + Hindi) NCERT Solutions

Table Of Content

• Ex.8.1
• Ex.8.2
• Ex.8.3
• Ex.8.4
• Introduction to Trigonometry Class 10 Important Questions
• Introduction to Trigonometry Class 10 Notes

Ex.8.1

Ex 8.1 Maths Question 1.
In ∆ABC right angled at B, AB = 24 cm, BC = 7 cm. Determine:
(i) sin A, cos A
(ii) sin C, cos C
Solution: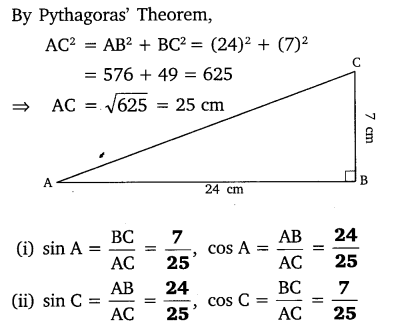

Ex 8.1 Class 10 Maths Question 2.
In given figure, find tan P – cot R.
Solution:

You can also download the free PDF of Chapter 8 Ex 8.1 Introduction to Trigonometry NCERT Solutions or save the solution images and take the print out to keep it handy for your exam preparation.

Download NCERT Solutions For Class 10 Maths Chapter 8 Introduction to Trigonometry PDF

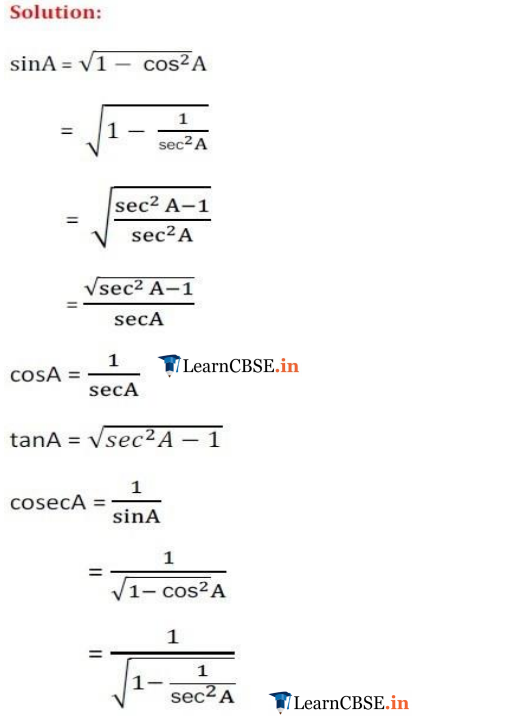
Ex 8.1 Class 10 Maths Question 3.
If sin A = 34 , calculate cos A and tan A.
Solution: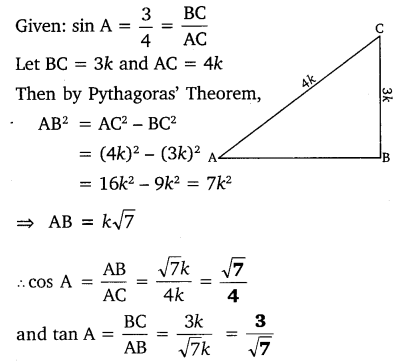

Ex 8.1 Class 10 Maths Question 4.
Given 15 cot A = 8, find sin A and sec A.
Solution:

Ex 8.1 Class 10 Maths Question 5.
Given sec θ = 1312 , calculate all other trigonometric ratios.
Solution:

Ex 8.1 Class 10 Maths Question 6.
If ∠A and ∠B are acute angles such that cos A = cos B, then show that ∠A = ∠B.
Solution:

Ex 8.1 Class 10 Maths Question 7.
If cot θ = 78, evaluate:
(i) (1+sinθ)(1−sinθ)(1+cosθ)(1−cosθ)
(ii) cot²θ
Solution:

Ex 8.1 Class 10 Maths Question 8.
If 3 cot A = 4, check whether 1−tan2A1+tan2A = cos² A – sin² A or not.
Solution:

Ex 8.1 Class 10 Maths Question 9.
In triangle ABC, right angled at B, if tan A = 1√3, find the value of:
(i) sin A cos C + cos A sin C
(ii) cos A cos C – sin A sin C
Solution:

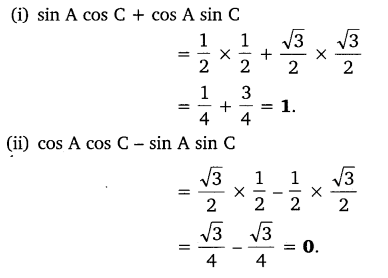
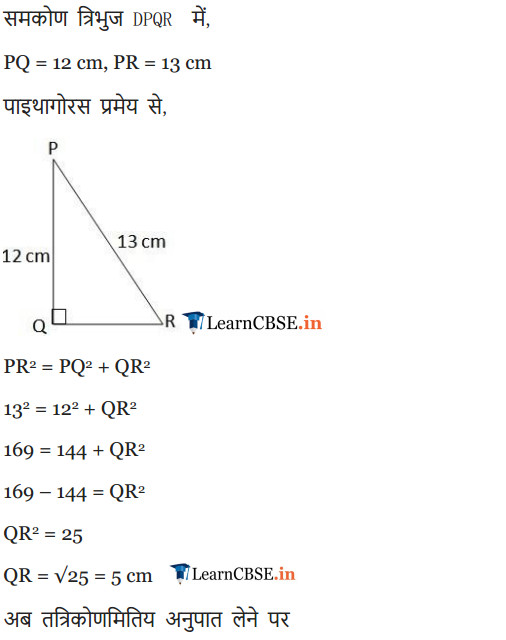
Ex 8.1 Class 10 Maths Question 10.
In ΔPQR, right-angled at Q, PR + QR = 25 cm and PQ = 5 cm. Determine the values of sin P, cos P and tan P.
Solution:

Ex 8.1 Class 10 Maths Question 11.
State whether the following statements are true or false. Justify your answer.
(i) The value of tan A is always less than 1.
(ii) sec A = 125 for some value of angle A.
(iii) cos A is the abbreviation used for the cosecant of angle A.
(iv) cot A is the product of cot and A.
(v) sin θ = 43 for some angle.
Solution:

Class 10 Maths Introduction To Trigonometry

Trigonometry

Trigonometry is the study of relationships between the sides and angles of a right-angled triangle.

Trigonometric Ratios

Trigonometric ratios of an acute angle in a right triangle express the relationship between the angle and the length of its sides.
Let ∆ABC be a triangle right angled at B. Then the trigonometric ratios of the angle A in right ∆ABC are defined as follows: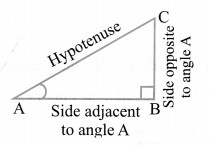

Note:
The values of the trigonometric ratios of an angle do not vary with the lengths of the sides of the triangle, if the angle remains same.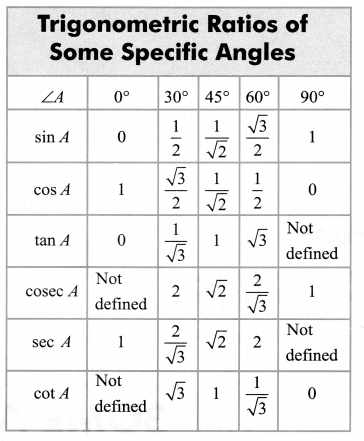

Trigonometric Ratios for Complementary Angles

sin (90° – A) = cos A
cos (90° – A) = sin A
tan (90° – A) = cot A
cot (90° – A) = tan A
sec (90° – A) = cosec A
cosec (90° – A) = sec A
Note:
Here (90° – A) is the complementary angle of A.

Trigonometric Identities

An equation involving trigonometric ratios of an angle is called a trigonometric identity, if it is true for all values of the angle(s) involved.
(i) sin2θ + cos2θ = 1 [for 0° ≤ θ ≤ 90°]
(ii) sec2θ – tan2θ = 1 [for 0° ≤ θ ≤ 90°]
(iii) cosec2θ – cot2θ = 1 [for 0° < θ ≤ 90°]

NCERT Solutions for Class 10 Maths Chapter 8 Introduction to Trigonometry (Hindi Medium) Ex 8.1

Class 10 Maths Chapter 8 Introduction to Trigonometry Ex 8.2

Ex 8.2 Class 10 Maths Question 1.

Evaluate the following:

Solution: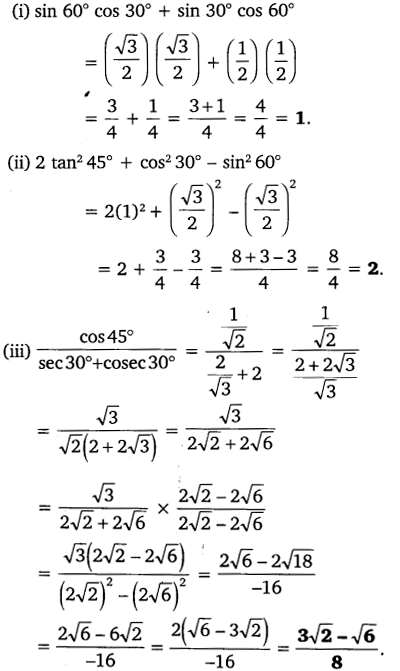

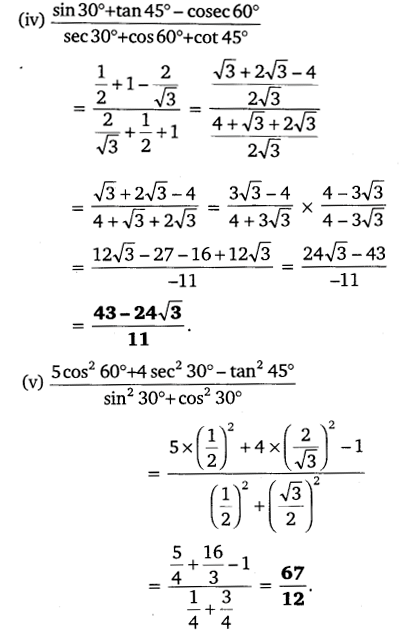
Ex 8.2 Class 10 Maths Question 2.
Choose the correct option and justify your choice: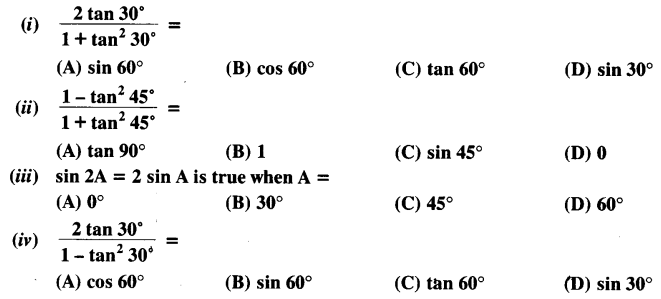

Solution:

Download NCERT Solutions For Class 10 Maths Chapter 8 Introduction to Trigonometry PDF

Ex 8.2 Class 10 Maths Question 3.
If tan (A + B) = √3 and tan (A – B) = 1√3; 0° < A + B ≤ 90°; A > B, find A and B.
Solution: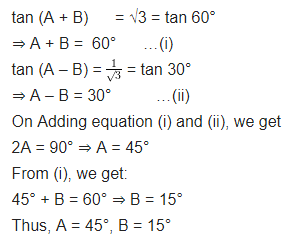

Ex 8.2 Class 10 Maths Question 4.
State whether the following statements are true or false. Justify your answer.
(i) sin (A + B) = sin A + sin B.
(ii) The value of sin θ increases as θ increases.
(iii) The value of cos θ increases as θ increases.
(iv) sin θ = cos θ for all values of θ.
(v) cot A is not defined for A = 0°.
Solution: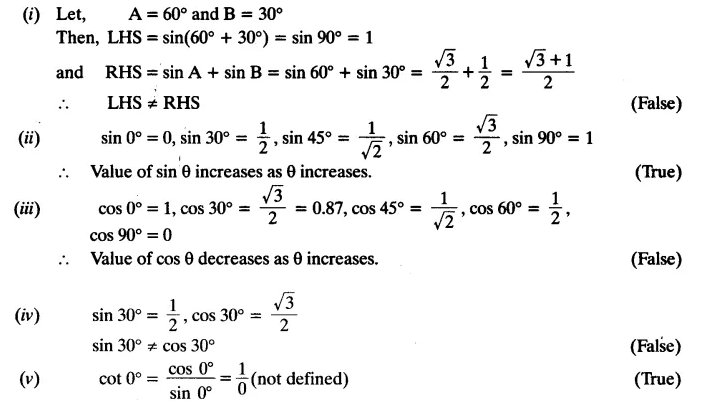

NCERT Solutions for Class 10 Maths Chapter 8 Introduction to Trigonometry (Hindi Medium) Ex 8.2

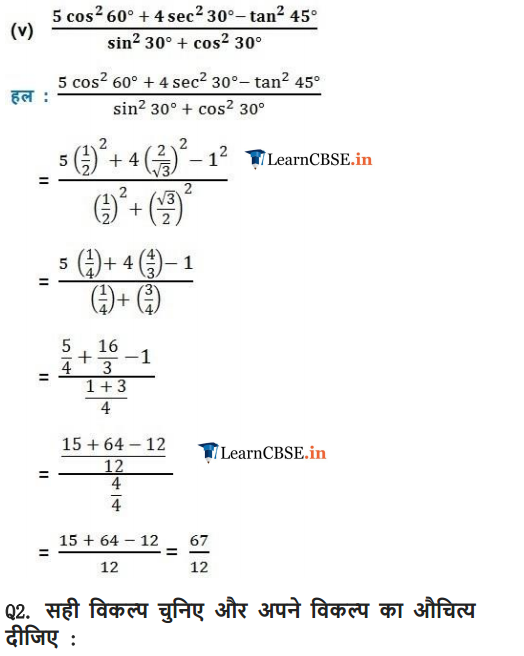
Class 10 Maths Chapter 8 Introduction to Trigonometry Ex 8.3

Ex 8.3 Class 10 Maths Question 1.

Evaluate:

Solution: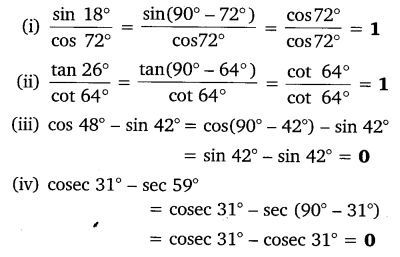

Ex 8.3 Class 10 Maths Question 2.
Show that:
(i) tan 48° tan 23° tan 42° tan 67° = 1
(ii) cos 38° cos 52° – sin 38° sin 52° = 0
Solution:

Ex 8.3 Class 10 Maths Question 3.

If tan 2A = cot (A – 18°), where 2A is an acute angle, find the value of A.
Solution: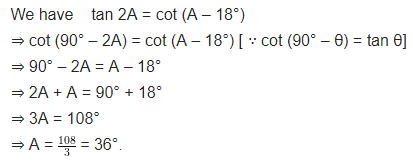

Ex 8.3 Class 10 Maths Question 4.
If tan A = cot B, prove that A + B = 90°.
Solution: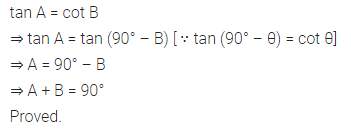

Ex 8.3 Class 10 Maths Question 5.
If sec 4A = cosec (A – 20°), where 4A is an acute angle, find the value of A.
Solution: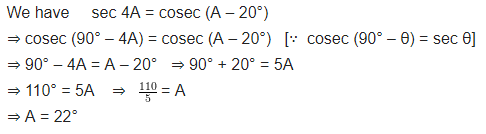

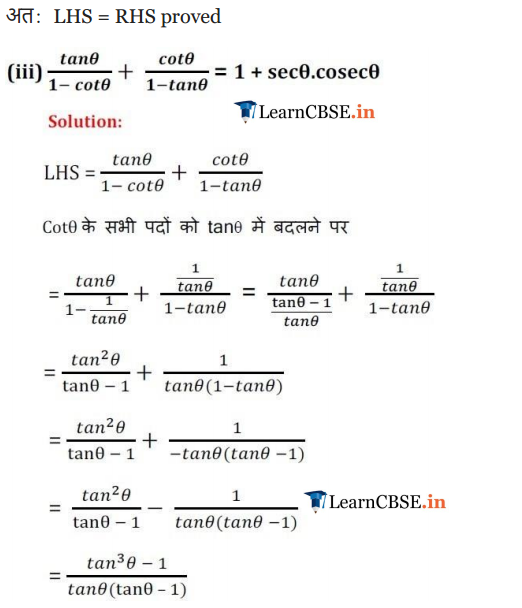
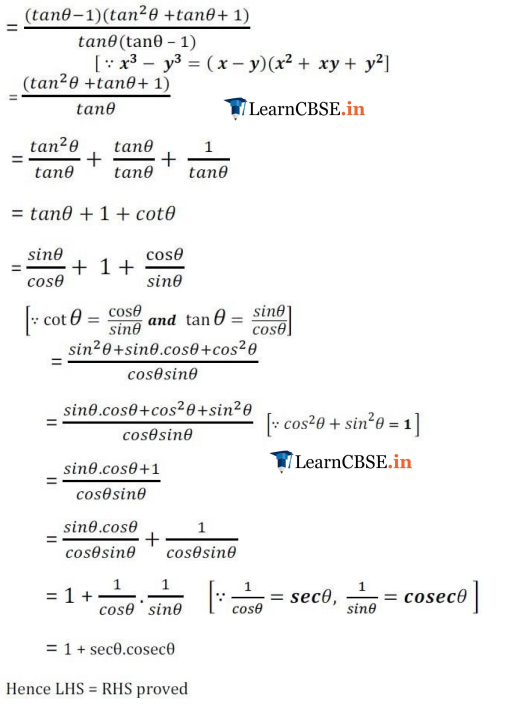
Ex 8.3 Class 10 Maths Question 6.
If A, B and C are interior angles of a triangle ABC, then show that: sin (B+C2) = cos A2
Solution: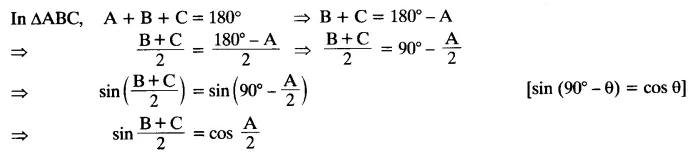

Ex 8.3 Class 10 Maths Question 7.
Express sin 61° + cos 75° in terms of trigonometric ratios of angles between 0° and 45°.
Solution:

NCERT Solutions for Class 10 Maths Chapter 8 Introduction to Trigonometry (Hindi Medium) Ex 8.3

Class 10 Maths Chapter 8 Introduction to Trigonometry Ex 8.4

NCERT Solutions for Class 10 Maths Chapter 8 Introduction to Trigonometry Ex 8.4 are part of NCERT Solutions for Class 10 Maths. Here we have given NCERT Solutions for Class 10 Maths Chapter 8 Introduction to Trigonometry Exercise 8.4

Ex 8.4 Class 10 Maths Question 1.

Express the trigonometric ratios sin A, sec A and tan A in terms of cot A.Solution:

Ex 8.4 Class 10 Maths Question 2.
Write all the other trigonometric ratios of ∠A in terms of sec A.
Solution: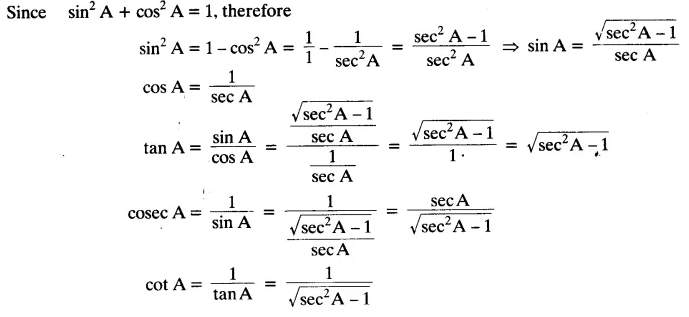

Ex 8.4 Class 10 Maths Question 3.

Evaluate: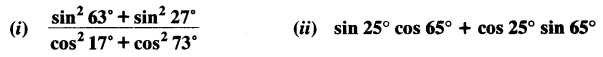

Solution: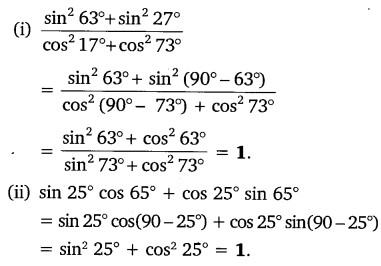

Ex 8.4 Class 10 Maths Question 4.
Choose the correct option. Justify your choice.
(i) 9 sec² A – 9 tan² A = ……
(A) 1
(B) 9
(C) 8
(D) 0

(ii) (1 + tan θ + sec θ) (1 + cot θ – cosec θ) = ………..
(A) 0
(B) 1
(C) 2
(D) -1

(iii) (sec A + tan A) (1 – sin A) = ………….
(A) sec A
(B) sin A
(C) cosec A
(D) cos A

(iv) 1+tan2A1+cot2A = ………..
(A) sec² A
(B) -1
(C) cot² A
(D) tan² A
Solution:

Ex 8.4 Class 10 Maths Question 5.
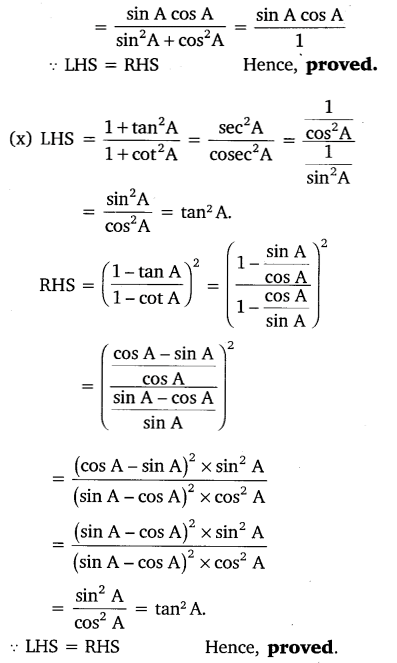
Prove the following identities, where the angles involved are acute angles for which the expressions are defined.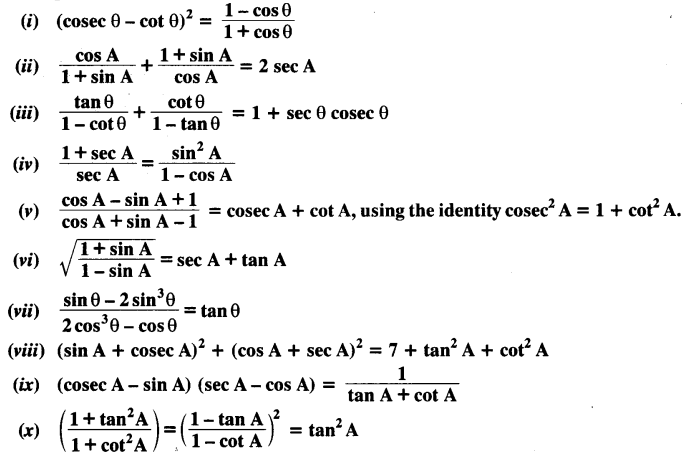

Solution:

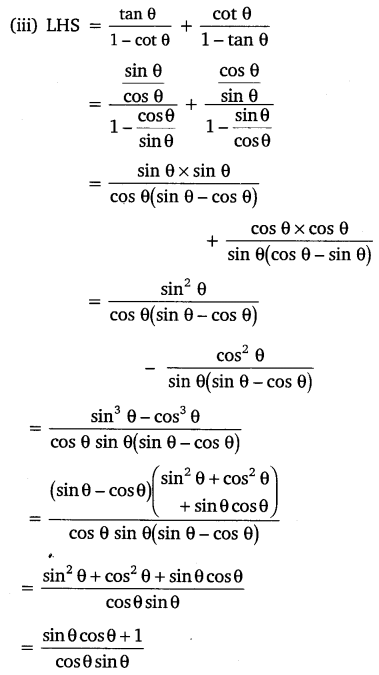
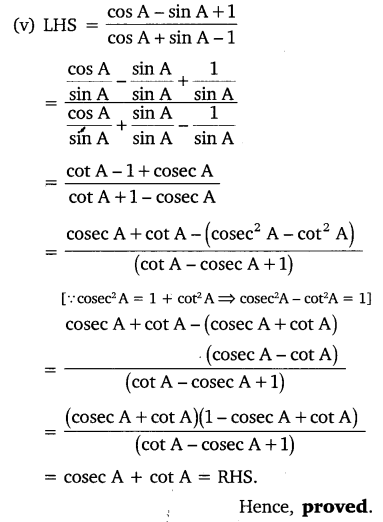
NCERT Solutions for Class 10 Maths Chapter 8 Introduction to Trigonometry (Hindi Medium) Ex 8.4

Important Questions for Class 10 Maths Chapter 8 Introduction to Trigonometry

Introduction to Trigonometry Class 10 Important Questions Very Short Answer (1 Mark)

Question 1.
If tan θ + cot θ = 5, find the value of tan2θ + cotθ. (2012)
Solution:
tan θ + cot θ = 5 … [Given
tan2θ + cot2θ + 2 tan θ cot θ = 25 … [Squaring both sides
tan2θ + cot2θ + 2 = 25
∴ tan2θ + cot2θ = 23

Question 2.
If sec 2A = cosec (A – 27°) where 2A is an acute angle, find the measure of ∠A. (2012, 2017D)
Solution:
sec 2A = cosec (A – 27°)
cosec(90° – 2A) = cosec(A – 27°) …[∵ sec θ = cosec (90° – θ)
90° – 2A = A – 27°
90° + 27° = 2A + A
⇒ 3A = 117°
∴ ∠A = 117∘3 = 39°

Question 3.
If tan α = 3–√ and tan β = 13√,0 < α, β < 90°, find the value of cot (α + β). (2012)
Solution:
tan α = 3–√ = tan 60° …(i)
tan β = 13√ = tan 30° …(ii)
Solving (i) & (ii), α = 60° and β = 30°
∴ cot (α + β) = cot (60° + 30°) = cot 90° = 0

Question 4.
If sin θ – cos θ = 0, find the value of sin4 θ + cos4 θ. (2012, 2017D)
Solution:
sin θ – cos θ = 0 = sin θ = cos θ
⇒ sinθ = 1 ⇒ tan θ = 1 ⇒ θ = 45°
Now, sin4θ + cos4θ
= sin4 45° + cos4 45°
= (12√)4+(12√)4=14+14=24=12

Question 5.
If sec θ + tan θ = 7, then evaluate sec θ – tan θ. (2017OD)
Solution:
We know that,
sec2θ – tan2θ = 1
(sec θ + tan θ) (sec θ – tan θ) = 1
(7) (sec θ – tan θ) = 1 …[sec θ + tan θ = 7; (Given)
∴ sec θ – tan θ = 17

Question 6.
Evaluate: 10. 1−cot245∘. (2014)
Solution:

Question 7.
If cosec θ = 54, find the value of cot θ. (2014)
Solution:
We know that, cot2θ = cosec2θ – 1
= (54)2 – 1 ⇒ 2516 – 1 ⇒ 25−1616
coť2θ = 916 i cot θ = 34

Question 8.
If θ = 45°, then what is the value of 2 sec2θ + 3 cosec2θ ? (2014)
Solution:
2 sec2θ + 3 cosec2θ = 2 sec2 45° + 3 cosec2 45°
= 2(2–√)2 + 3 (2–√)2 = 4 + 6 = 10

Question 9.
If 3–√ sin θ = cos θ, find the value of 3cos2θ+2cosθ. (2015)
Solution:
3–√ sin θ = cos θ … [Given

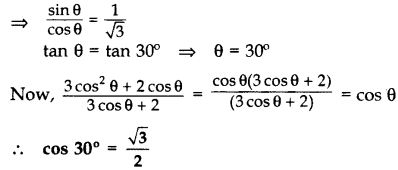
Question 10.
Evaluate: sin2 19° + sin771°. (2015)
Solution:
sin2 19° + sin2 71°
= sin219° + sin2 (90° – 19°)…[∵ sin(90° – θ) = cos θ
= sin2 19° + cos2 19° = 1 …[∵ sin2 θ + cos2 θ = 1

Question 11.
What happens to value of cos when increases from 0° to 90°? (2015)
Solution:
cos 0° = 1, cos 90° = 0
When θ increases from 0° to 90°, the value of cos θ decreases from 1 to 0.

Question 12.
If tan θ = ax, find the value of xa2+x2√. (2013)
Solution: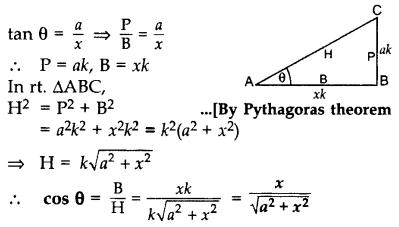

Question 13.
If in a right angled ∆ABC, tan B = 125, then find sin B. (2014)
Solution:
1st method:
tan B = 125 ∴ cot B = 512
cosec2 B = 1 + cot2 B
= 1 + [(512)2/latex]=1+[latex]
= 144+25144=169144
cosec B = 1312 ∴ sin B = 1213
2nd method: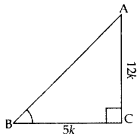

tan B = 125
tan B = ACBC
Let AC = 12k, BC = 5k
In rt. ∆ACB,
AB2 = AC2 + BC2 …[Pythagoras theorem
AB2 = (12k)2 + (5k)2
AB2 = 144k2 + 25k22 = 169k2
AB = 13k
∴ sin B = ACAB=12k13k=1213

Question 14.
If ∆ABC is right angled at B, what is the value of sin (A + C). (2015)
Solution: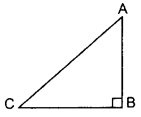

∠B = 90° …[Given
∠A + ∠B + ∠C = 180° …[Angle sum property of a ∆
∠A + ∠C + 90° = 180°
∠A + ∠C = 90°
∴ sin (A + C) = sin 90° = 1 …(taking sin both side

Introduction to Trigonometry Class 10 Important Questions Short Answer-I (2 Marks)

Question 15.
Evaluate: tan 15° . tan 25° , tan 60° . tan 65° . tan 75° – tan 30°. (2013)
Solution:
tan 15°. tan 25°, tan 60°. tan 65°. tan 75° – tan 30°
= tan(90° – 75°) tan(90° – 65°). 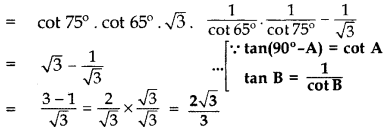3–√ . tan 65°. tan 75° – 13√

Question 16.
Express cot 75° + cosec 75° in terms of trigonometric ratios of angles between 0° and 30°. (2013)
Solution:
cot 75° + cosec 75°
= cot(90° – 15°) + cosec(90° – 15°)
= tan 15° + sec 15° …[cot(90°-A) = tan A
cosec(90° – A) = sec A

Question 17.
If cos (A + B) = 0 and sin (A – B) = 3, then find the value of A and B where A and B are acute angles. (2012)
Solution: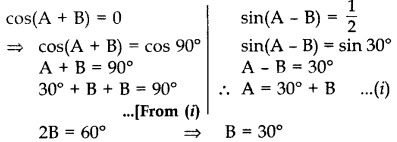

Putting the value of B in (i), we get
⇒ A = 30° + 30° = 60°
∴ A = 60°, B = 30°

Question 18.
If A, B and C are the interior angles of a ∆ABC, show that sin (A+B2) = cos(c2). (2012)
Solution:
In ∆ABC, ∠A + ∠B + ∠C = 180° …(Angle sum property of ∆
∠A + ∠B = 180° – ∠C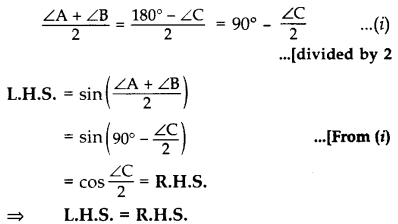

Question 19.
If x = p sec θ + q tan θ and y = p tan θ + q sec θ, then prove that x2 – y2 = p2 – q2. (2014)
Solution:
L.H.S. = x2 – y2
= (p sec θ + q tan θ)2 – (p tan θ + q sec θ)2
= p2 sec θ + q2 tan2 θ + 2 pq sec 2 tan 2 -(p2 tan2 θ + q2 sec2 θ + 2pq sec θ tan θ)
= p2 sec θ + 2 tan2 θ + 2pq sec θ tan θ – p2 tan2 θ – q2 sec θ – 2pq sec θ tan θ
= p2(sec2 θ – tan2 θ) – q2(sec?2 θ – tan2 θ) =
= p2 – q2 …[sec2 θ – tan2 θ = 1
= R.H.S.

Question 20.
Prove the following identity: (2015)
sin3θ+cos3θ = 1 – sin θ . cos θ
Solution: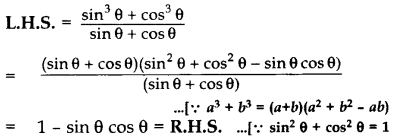

Question 21.
Simplify: 1+tan2A. (2014)
Solution: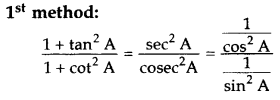

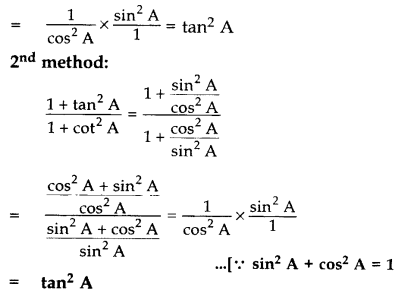
Question 22.
If x = a cos θ – b sin θ and y = a sin θ + b cos θ, then prove that a2 + b2 = x2 + y2. (2015)
Solution:
R.H.S. = x2 + y2
= (a cos θ – b sin θ)2 + (a sin θ + b cos θ)2
= a2cos2 θ + b2 sin2 θ – 2ab cos θ sin θ + a2 sin2 θ + b2 cos2 θ + 2ab sin θ cos θ
= a2(cos2 θ + sin2θ) + b2 (sin2 θ + cos2 θ)
= a2 + b2 = L.H.S. …[∵ cos2 θ + sin2 θ = 1

Introduction to Trigonometry Class 10 Important Questions Short Answer – II (3 Marks)

Question 23.
Given 2 cos 3θ = 3–√, find the value of θ. (2014)
Solution:
2 cos 3θ = 3–√ …[Given
cos 3θ = 3√2 ⇒ cos 3θ = cos 30°
30 = 30° ∴ θ = 10°

Question 24.
If cos x = cos 40° . sin 50° + sin 40°. cos 50°, then find the value of x. (2014)
Solution:
cos x = cos 40° sin 50° + sin 40° cos 50°
cos x = cos 40° sin(90° – 40°) + sin 40°.cos(90° – 40°)
cos x = cos2 40° + sin2 40°
cos x = 1 …[∵ cos2 A + sin2 A = 1
cos x = cos 0° ⇒ x = 0°

Question 25.
If sin θ = 12, then show that 3 cos θ – 4 cos3 θ = 0. (2014)
Solution:
sin θ = 12
sin θ = sin 30° ⇒ θ = 30°
L.H.S = 3 cos θ – 4 cos3 θ
= 3 cos 30° – 4 cos3(30°)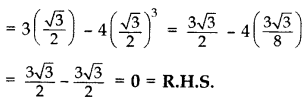

Question 26.
If 5 sin θ = 4, prove that 1cosθ+1cotθ = 3 (2013
Solution:
Given: 5 sin θ = 4

Question 27.
Evaluate: sec 41°. sin 49° + cos 29°.cosec 61° 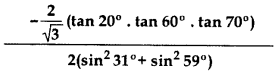 (2012)
Solution:

Question 28.
Evaluate: (2012, 2017D)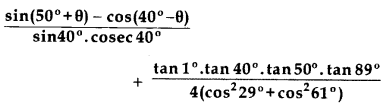

Solution: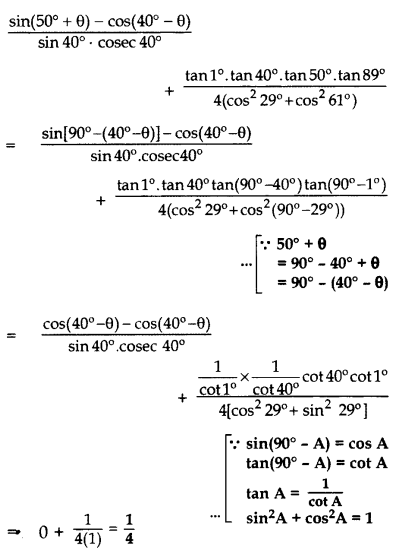

Question 29.
In figure, ∆PQR right angled at Q, PQ = 6 cm and PR = 12 cm. Determine ∠QPR and ∠PRQ. (2013)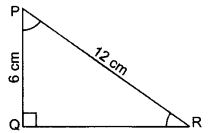

Solution:
In rt. ∆PQR,
PQ2 + QR2 = PR2 …[By Pythogoras’ theorem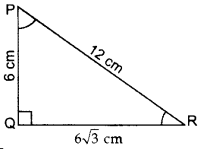

(6)2 + QR2 = (12)2
QR2 = 144 – 36
QR2 = 108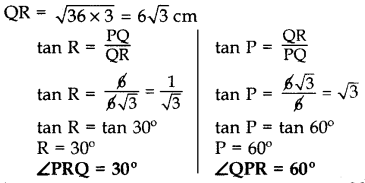

Question 30.
Find the value of: (2013)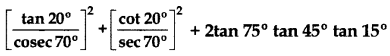

Solution:

Question 31.
Prove that: sin263∘+sin227∘ + 2 sin 36° sin 42° sec 48° sec 54° (2017OD)
Solution:

Question 32.
If sin θ = 1213, 0° <0 < 90°, find the value of: sin2θ−cos2θ2sinθ⋅cosθ×1tan2θ (2015)
Solution:

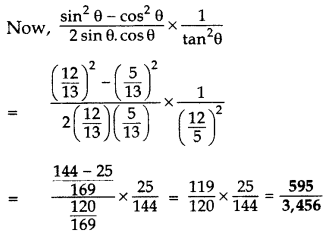
Question 33.
Prove that: (2012)

Solution: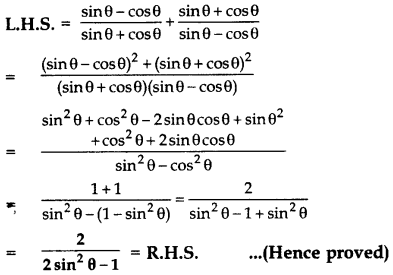

Question 34.
Prove that: tanθ+secθ−1tanθ−secθ+1=1+sinθcosθ (2012, 2017D)
Solution: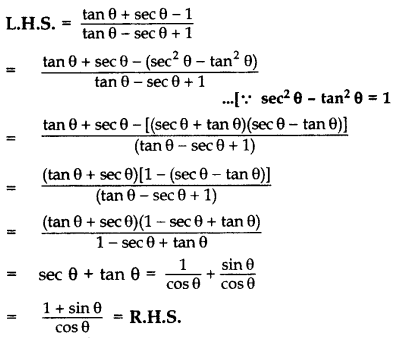

Question 35.
If tan θ = ab, prove that asinθ−bcosθasinθ+bcosθ=a2−b2a2+b2 (2013)
Solution:

Question 36.
Prove the identity: (sec A – cos A). (cot A + tan A) = tan A . sec A. (2014)
Solution:
L.H.S.= (sec A – cos A) (cot A + tan A)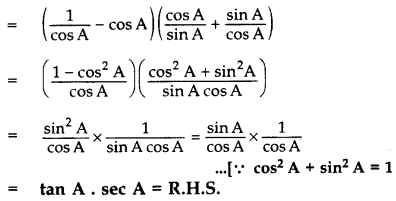

Question 37.
If sec θ + tan θ = p, prove that sin θ = p2−1p2+1 (2015)
Solution: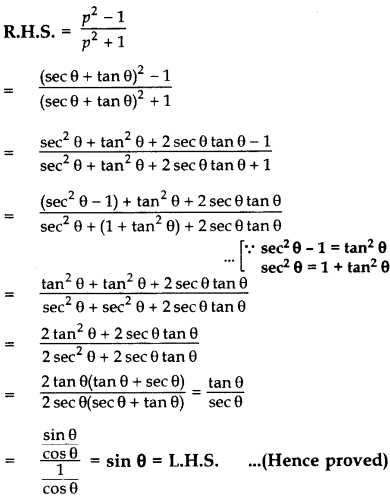

Question 38.
Prove that: sinθ−2sin3θ = tan θ (2015)
Solution: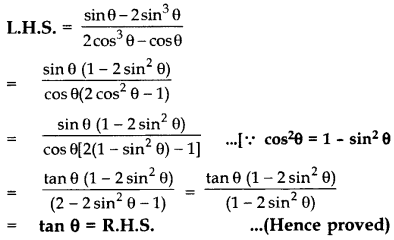

Question 39.
Prove that: sinθ1+cosθ+1+cosθsinθ = 2 cosec θ (2017OD)
Solution:

Introduction to Trigonometry Class 10 Important Questions Long Answer (4 Marks)

Question 40.
In an acute angled triangle ABC, if sin (A + B – C) = 12 and cos (B + C – A) = 12√, find ∠A, ∠B and ∠C. (2012)
Solution:

Putting the values of A and B in (iii), we get
67.5° + B + 75o = 180°
B = 180° – 67.5° – 75o = 37.5°
∴ ∠A = 67.5°, ∠B = 37.5° and ∠C = 75°

Question 41.
Evaluate: (2013)

Solution: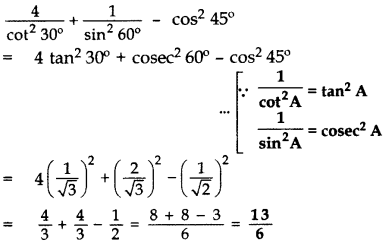

Question 42.
Evaluate the following: (2015)

Solution: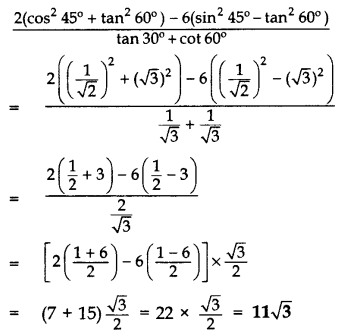

Question 43.
If θ = 30°, verify the following: (2014)
(i) cos 3θ = 4 cos3 θ – 3 cos θ
(ii) sin 3θ = 3 sin θ – 4 sin3θ
Solution: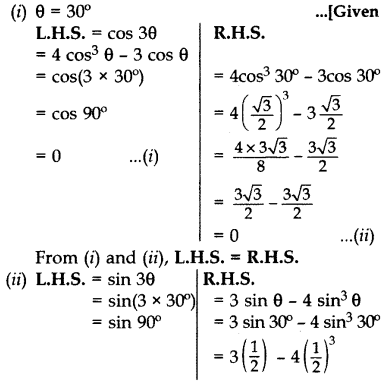

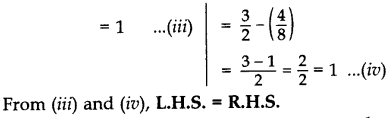
Question 44.
If tan (A + B) = 3–√ and tan (A – B) = 13√ where 0 < A + B < 90°, A > B, find A and B. Also calculate: tan A. sin (A + B) + cos A. tan (A – B). (2015)
Solution:

Question 45.
Find the value of cos 60° geometrically. Hence find cosec 60°. (2012, 2017D)
Solution: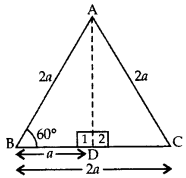

Let ∆ABC be an equilateral ∆.
Let each side of triangle be 2a.
Since each angle in an equilateral ∆ is 60°
∴ ∠A = ∠B = ∠C = 60°
Draw AD ⊥ BC
In ∆ADB and A∆ADC,
AB = AC … [Each = 2a
AD = AD …[Common
∠1 -∠2 … [Each 90°
∴ ∆ADB = ∆ADC …[RHS congruency rule
BD = DC = 2a2 = a
In rt. ∆ADB, cos 60° = 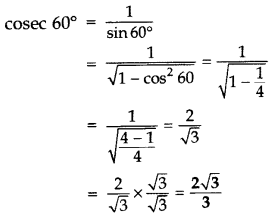BDAB=a2a=12

Question 46.
If tan(20° – 3α) = cot(5α – 20°), then find the value of α and hence evaluate: sin α. sec α . tan α – cosec α . cos α . cot α. (2014)
Solution:
tan(20° – 3α) = cot(5α – 20°)
tan(20° – 3α) = tan[90° – (5α – 20°)] …[∵ cot θ = tan(90° – θ)]
∴ 20° – 3α = 90° – 5α + 20°
⇒ -3α + 5α = 90° + 20° – 20°
⇒ 2α = 90° ⇒ α = 45°
Now, sin α . sec α tan α – cosec α . cos α . cot α
= sin 45°. sec 45° tan 45° – cosec 45°. cos 45° cot 45°
= 12√×2–√×1−2–√×12√×1=1−1=0

Question 47.
If xacosθ + ybsinθ = 1 and xasinθ – yb cosθ = 1, prove that event x2a2+y2b2 = 2. (2012, 2017D)
Solution:

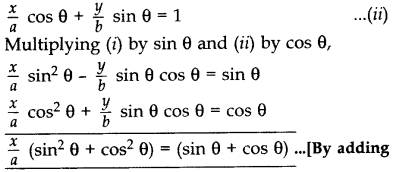
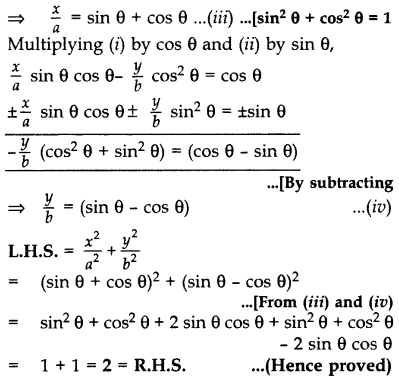
Question 48.
If sin θ = cc2+d2√ and d > 0, find the values of cos θ and tan θ. (2013)
Solution:

Question 49.
If cot B = 125, prove that tan2B – sin2B = sin4 B . sec2 B. (2013)
Solution:
cot B = 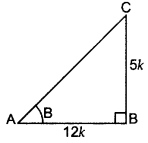125 :: ABBC=125

AB = 12k, BC = 5k
In rt. ∆ABC, …[By Pythagoras’ theorem
AC2 = AB2 + BC2
AC2 = (12k)2 + (5k)2
AC2 = 144k2 + 25k2
AC2 = 169k2
AC = +13k …[∵ Hypotenuse cannot be -ve

Question 50.
If 3–√ cot2θ – 4 cot θ + 3–√ = 0, then find the value of cot2 θ + tan2θ. (2013)
Solution: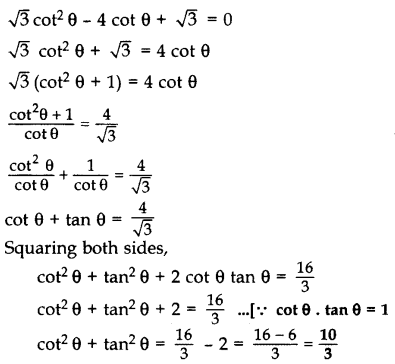

Question 51.
Prove that b2x2 – a2y2 = a2b2, if: (2014)
(i) x = a sec θ, y = b tan θ
(ii) x = a cosec θ, y = b cot θ
Solution:
(i) L.H.S. = b2x2 – a2y2
= b2(a sec θ)2 – a2(b tan θ)2
= b2a2 sec θ – a2b2 tan2θ
= b2a2(sec2 θ – tan2 θ)
= b2a2(1) …[∵ sec2θ – tan2 θ = 1
= a2b2 = R.H.S.

(ii) L.H.S. = b2x2 – a2y2
= b2(a cosec θ)2 – a2(b cot θ)2
= b2a2 cosec2 θ – a2b2 cot2 θ
= b2a2(cosec2θ – cot2 θ)
= b2a2 (1) ..[∵ cosec2 θ – cot2 θ = 1
= a2b2= R.H.S.

Question 52.
If sec θ – tan θ = x, show that sec θ + tan θ = 1x and hence find the values of cos θ and sin θ. (2015)
Solution:

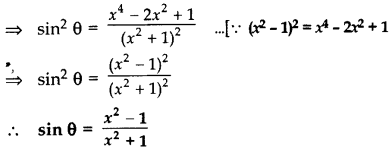
Question 53.
If cosec θ + cot θ = p, then prove that cos θ = p2−1p2+1. (2012)
Solution:
cosec θ + cot θ = p

Question 54.
If tan θ + sin θ = p; tan θ – sin θ = q; prove that p2 – q2 = 4pq−−√. (2012)
Solution:
L.H.S. = p2 – q2
= (tan θ + sin θ)2 – (tan θ – sin θ)2
= (tan2θ + sin2θ + 2.tanθ.sinθ) – (tan2θ + sin2θ – 2tan θ sin θ)
= 2 tan θ sin θ+ 2 tan θ sin θ
= 4 tan θ sin θ …(i)

Question 55.
If sin θ + cos θ = m and sec θ + cosec θ = n, then prove that n(m2 – 1) = 2m. (2013)
Solution:
m2 – 1 = (sin θ + cos θ)2 – 1
= sin2 θ + cos2θ + 2 sin θ cos θ – 1
= 1 + 2 sin θ cos θ – 1
= 2 sin θ cos θ …[sin2 θ + cos2 θ = 1
L.H.S. = n(m2 – 1)
= (sec θ + cosec θ) 2 sin θ cos θ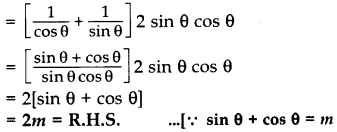

Question 56.
Prove that: 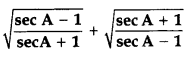 = 2 cosec A (2012)
Solution: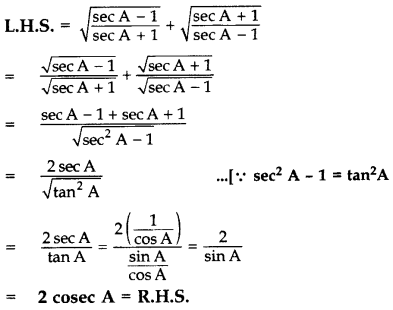

Question 57.
In ∆ABC, show that sin2 A2 + sin2 B+C2 = 1. (2013)
Solution:
In ∆ABC, ∠A + ∠B + ∠C = 180° … [Sum of the angles of ∆
∠B + ∠C = 180° – ∠A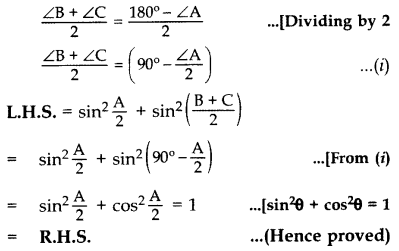

Question 58.
Find the value of: (2013)

Solution: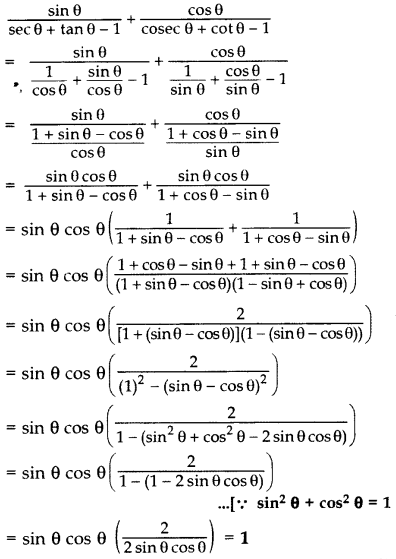

Question 59.
Prove that: (sin θ + cos θ + 1). (sin θ – 1 + cos θ) . sec θ . cosec θ = 2 (2014)
Solution:
L.H.S. = (sin θ + cos θ + 1) (sin θ – 1 + cos θ) . sec θ cosec θ
= [(sin θ + cos θ) + 1] [(sin θ + cos θ) – 1] . sec θ cosec θ
= [(sin θ + cos θ)2 – (1)2] sec θ cosec θ …[∵ (a + b)(a – b) = a2 – b2
= (sin2 θ + cos2θ + 2 sin θ cos θ – 1]. sec θ cosec θ
= (1 + 2 sin θ cos θ – 1). sec θ cosecθ …[∵ sin2θ + cos2θ = 1
= (2 sin θ cos θ). 1cosθ⋅1sinθ
= 2 = R.H.S. …(Hence proved)

Question 60.
Prove that: (2014)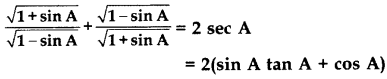

Solution:

Question 61.
Prove that: (1 + cot A + tan A). (sin A – cos A) = sec3A−csc3A (2015)
Solution:

Question 62.
Prove the identity: (2015)

Solution:

Question 63.
Prove the following trigonometric identities: sin A (1 + tan A) + cos A (1 + cot A) = sec A + cosec A. (2015)
Solution:
L.H.S.
= sin A (1 + tan A) + cos A (1 + cot A)

Question 64.
Prove that: (cot A + sec B)2 – (tan B – cosec A)2 = 2(cot A . sec B + tan B. cosec A) (2014)
Solution:
L.H.S.
= (cot A + sec B)2 – (tan B – cosec A)2
= cot2 A + sec2 B + 2 cot A sec B – (tan2 B + cosec2 A – 2 tan B cosec A)
= cot2 A + sec2 B + 2 cot A sec B – tan2 B – cosec2 A + 2 tan B cosec A
= (sec2 B – tan2 B) – (cosec2 A – cot2 A) + 2(cot A sec B + tan B cosec A)
= 1 – 1 + 2(cot A sec B + tan B cosec A) … [∵ sec2B – tan2 B = 1
cosec2A – cot2 A = 1
= 2(cot A . sec B + tan B . cosec A) = R.H.S.

Question 65.
If x = r sin A cos C, y = r sin A sin C and z = r cos A, then prove that x2 + y2 + z2 = r2. (2017OD)
Solution:
x = r sin A cos C; y = r sin A sin C; z = r cos A
Squaring and adding,
L.H.S. x2 + y2 + z2 = 2 sin2 A cos2C + r2 sin2 A sin2 C + r2 cos2 A
= r2 sin2 A(cos2 C + sin2 C) + r2 cos2 A
= r2 sin2 A + r2 cos2 A … [cos2θ + sin2θ = 1
= r2 (sin2 A + cos2 A) = r2 = R.H.S.

Question 66.
Prove that: (2017OD)

Solution: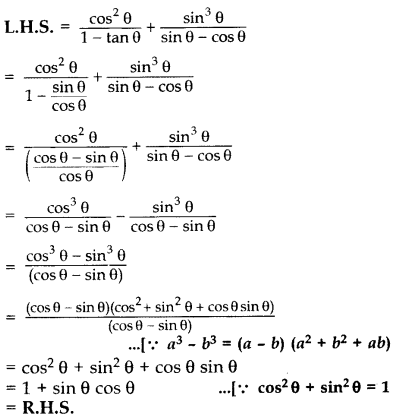

Question 67.
In the adjoining figure, ABCD is a rectanlge with breadth BC = 7 cm and ∠CAB = 30°. Find the length of side AB of the rectangle and length of diagonal AC. If the ∠CAB = 60°, then what is the size of the side AB of the rectangle. [Use 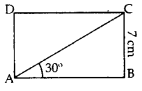3–√ = 1.73 and 2–√ = 1.41, if required) (2014OD)

Solution: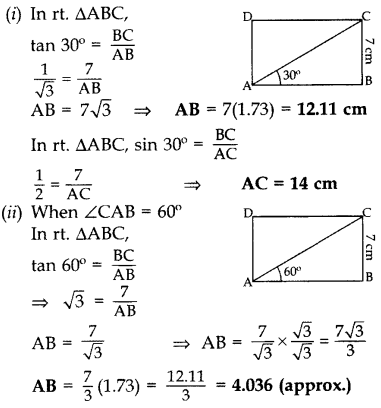

Class 10 Maths Notes Chapter 8 Introduction to Trigonometry

• Position of a point P in the Cartesian plane with respect to co-ordinate axes is represented by the ordered pair (x, y).
• Trigonometry is the science of relationships between the sides and angles of a right-angled triangle.
• Trigonometric Ratios: Ratios of sides of right triangle are called trigonometric ratios.
  Consider triangle ABC right-angled at B. These ratios are always defined with respect to acute angle ‘A’ or angle ‘C.
• If one of the trigonometric ratios of an acute angle is known, the remaining trigonometric ratios of an angle can be easily determined.
• How to identify sides: Identify the angle with respect to which the t-ratios have to be calculated. Sides are always labelled with respect to the ‘θ’ being considered.

Let us look at both cases: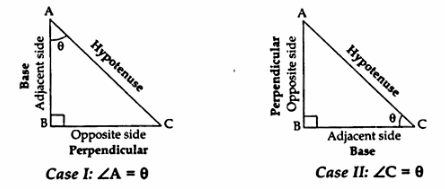

In a right triangle ABC, right-angled at B. Once we have identified the sides, we can define six t-Ratios with respect to the sides.

case I	case II
(i) sine A = perpendicularhypotenuse=BCAC	(i) sine C = perpendicularhypotenuse=ABAC
(ii) cosine A = basehypotenuse=ABAC	(ii) cosine C = basehypotenuse=BCAC
(iii) tangent A = perpendicularbase=BCAB	(iii) tangent C = perpendicularbase=ABBC
(iv) cosecant A = hypotenuseperpendicular=ACBC	(iv) cosecant C = hypotenuseperpendicular=ACAB
(v) secant A = hypotenusebase=ACAB	(v) secant C = hypotenusebase=ACBC
(v) cotangent A = baseperpendicular=ABBC	(v) cotangent C = baseperpendicular=BCAB

Note from above six relationships:

cosecant A = 1sinA, secant A = 1cosineA, cotangent A = 1tanA,

However, it is very tedious to write full forms of t-ratios, therefore the abbreviated notations are:
sine A is sin A
cosine A is cos A
tangent A is tan A
cosecant A is cosec A
secant A is sec A
cotangent A is cot A

TRIGONOMETRIC IDENTITIES

An equation involving trigonometric ratio of angle(s) is called a trigonometric identity, if it is true for all values of the angles involved. These are:
tan θ = sinθcosθ
cot θ = cosθsinθ

• sin² θ + cos² θ = 1 ⇒ sin² θ = 1 – cos² θ ⇒ cos² θ = 1 – sin² θ
• cosec² θ – cot² θ = 1 ⇒ cosec² θ = 1 + cot² θ ⇒ cot² θ = cosec² θ – 1
• sec² θ – tan² θ = 1 ⇒ sec² θ = 1 + tan² θ ⇒ tan² θ = sec² θ – 1
• sin θ cosec θ = 1 ⇒ cos θ sec θ = 1 ⇒ tan θ cot θ = 1

ALERT:
A t-ratio only depends upon the angle ‘θ’ and stays the same for same angle of different sized right triangles.

Value of t-ratios of specified angles:

∠A	0°	30°	45°	60°	90°
sin A	0	12	12√	3√2	1
cos A	1	3√2	12√	12	0
tan A	0	13√	1	√3	not defined
cosec A	not defined	2	√2	23√	1
sec A	1	23√	√2	2	not defined
cot A	not defined	√3	1	13√	0

The value of sin θ and cos θ can never exceed 1 (one) as opposite side is 1. Adjacent side can never be greater than hypotenuse since hypotenuse is the longest side in a right-angled ∆.

‘t-RATIOS’ OF COMPLEMENTARY ANGLES

If ∆ABC is a right-angled triangle, right-angled at B, then
∠A + ∠C = 90° [∵ ∠A + ∠B + ∠C = 180° angle-sum-property]
or ∠C = (90° – ∠A)

Thus, ∠A and ∠C are known as complementary angles and are related by the following relationships:
sin (90° -A) = cos A; cosec (90° – A) = sec A
cos (90° – A) = sin A; sec (90° – A) = cosec A
tan (90° – A) = cot A; cot (90° – A) = tan A

Here Is The Class 10 Maths All NCERT Solutions In Hindi + English With Extra Questions, Notes And Important Questions

• Chapter 1 Real Numbers
• Chapter 2 Polynomials
• Chapter 3 Pair of Linear Equations in Two Variables
• Chapter 4 Quadratic Equations
• Chapter 5 Arithmetic Progressions
• Chapter 6 Triangles
• Chapter 7 Coordinate Geometry
• Chapter 8 Introduction to Trigonometry
• Chapter 9 Applications of Trigonometry
• Chapter 10 Circle
• Chapter 11 Constructions
• Chapter 12 Areas related to Circles
• Chapter 13 Surface Areas and Volumes
• Chapter 14 Statistics
• Chapter 15 Probability