Class 10 Maths Chapter 10 Circles (English + Hindi) NCERT Solutions

Class 10 Maths Chapter 10 Circles (English + Hindi) NCERT Solutions

• Ex.10.1
• Ex.10.2
• Applications of Trigonometry Class 10 Extra Questions
• Some Applications of Trigonometry Class 10 Important Questions
• Some Applications of Trigonometry Class 10 Notes

Ex 10.1

Ex 10.1 Class 10 Maths Question 1.
How many tangents can a circle have?
Solution:
There can be infinitely many tangents to a circle.

Ex 10.1 Class 10 Maths Question 2.
Fill in the blanks:
(i) A tangent to a circle intersects it in ………… point(s).
(ii) A line intersecting a circle in two points is called a ………… .
(iii) A circle can have ………………. parallel tangents at the most.
(iv) The common point of a tangent to a circle and the circle is called ……….. .
Solution:

You can also download the free PDF of  Ex 10.1 Class 10 Circles NCERT Solutions or save the solution images and take the print out to keep it handy for your exam preparation.

Download NCERT Solutions For Class 10 Maths Chapter 10 Circles PDF

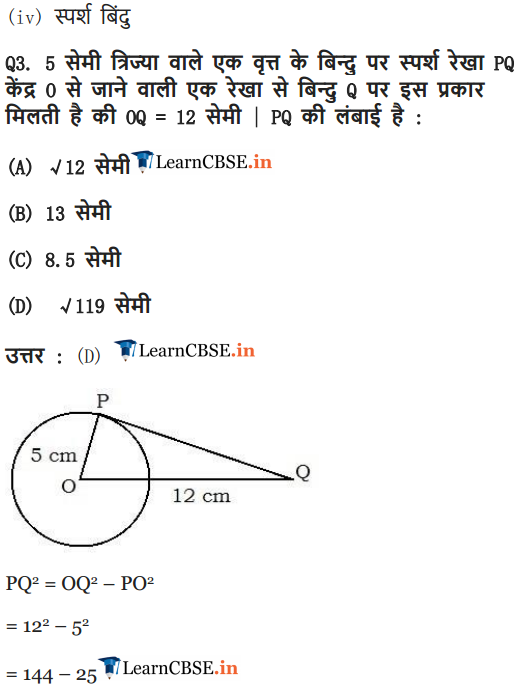
Ex 10.1 Class 10 Maths Question 3.
A tangent PQ at a point P of a circle of radius 5 cm meets a line through the centre O at a point Q so that OQ = 12 cm. Length PQ is
(a) 12 cm
(b) 13 cm
(c) 8.5 cm
(d) 119−−−√ cm
Solution: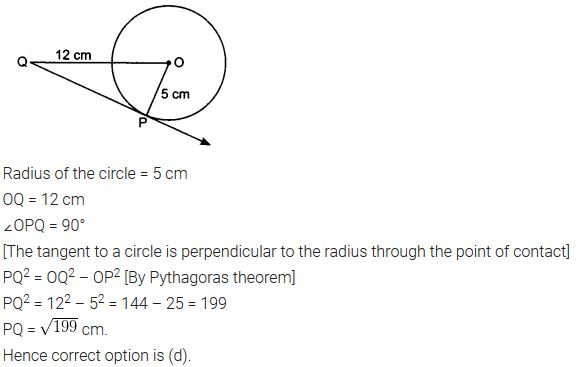

Note: PQ = √119

Ex 10.1 Class 10 Maths Question 4.
Draw a circle and two lines parallel to a given line such that one is a tangent and the other, a secant to the circle.
Solution: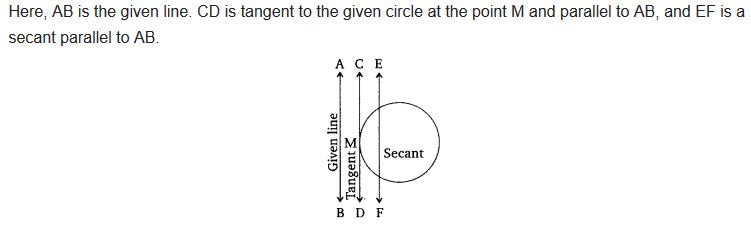

Class 10 Maths Circles Mind Map

Introduction

A circle is a set of all points in a plane at a fixed distance from a fixed point in a plane. The fixed point is called the centre of the circle. The fixed distance is called the radius of the circle.

Line and a Circle

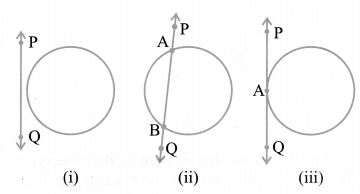
In Fig. (i), the line PQ and the circle have no common point. In this case, PQ is called a non-intersecting line with respect to the circle. In Fig. (ii), there are two common points A and B that the line PQ and the circle have. In this case, we call the line PQ a secant of the circle. In Fig. (iii), there is only one point A which is common to the line PQ and the circle. In this case, the line is called a tangent to the circle.

Tangent

A tangent to a circle is a straight line which touches the circle at only one point. The point where the tangent touches the circle is called point of contact of the tangent to the circle.
A tangent to a circle is a special case of a secant, when the two ends points of its corresponding chord coincides.
Theorem: Tangent at any point on a circle is perpendicular to the radius through the point of contact.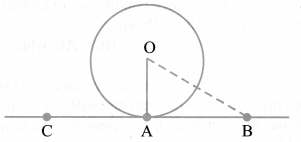

CB is the tangent to the given circle touching at A and OA is the radius.
∴ ∠OAB = 90°
(i) At any point on the circle there can be one and only one tangent.
(ii) The line containing the radius through the point of contact is called the normal to the circle at the point.

Number of Tangents from a Point to Circle

(i) No tangent can be drawn from the point lying inside the circle, as shown in fig. (i)
(ii) One and only one tangent can be drawn from a point lying on the circle, as shown in fig. (ii)
(iii) Only two tangents can be drawn from an exterior point to a circle, as shown in fig. (iii)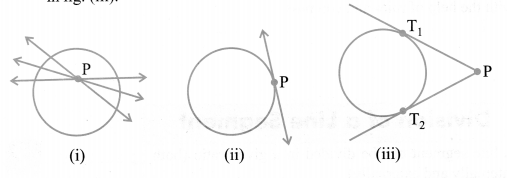

Length of a Tangent

The length of the segment of a tangent from an external point to the point of contact with the circle is called the length of the tangent

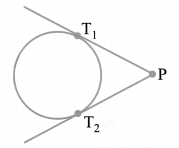
In the given figure, T1 and T2 are the points of contact of the tangents PT1 and PT2 respectively from the external point P.

Theorem Related to Length of Tangents From the External Points

The lengths of tangents drawn from an external point to a circle are equal.
i.e.,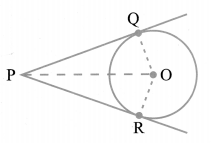

Here, PQ and PR are the two tangents drawn from P to the circle

NCERT Solutions for Class 10 Maths Chapter 10 Circles (Hindi Medium) Ex 10.1

Class 10 Maths Chapter 10 Circles Ex 10.2

NCERT Solutions for Class 10 Maths Chapter 10 Circles Ex 10.2 are part of NCERT Solutions for Class 10 Maths. Here we have given NCERT Solutions for Class 10 Maths Chapter 10 Circles Ex 10.2

In Q.1 to 3 choose the correct option and give justification.

Ex 10.2 Class 10 Maths Question 1.
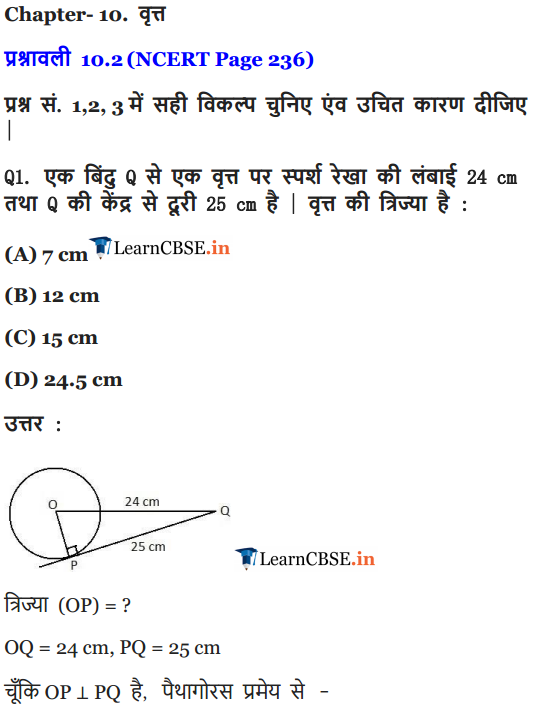
From a point Q, the length of the tangent to a circle is 24 cm and the distance of Q from the centre is 25 cm. The radius of the circle is
(a) 7 cm
(b) 12 cm
(c) 15 cm
(d) 24.5 cm
Solution: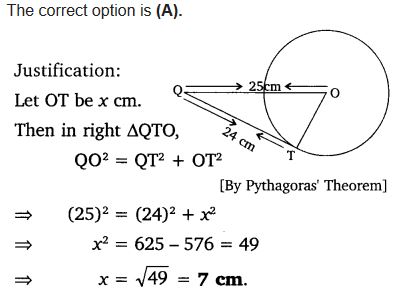

Ex 10.2 Class 10 Maths Question 2.
In figure, if TP and TQ are the two tangents to a circle with centre O so that ∠POQ = 110°, then ∠PTQ is equal to
(a) 60°
(b) 70°
(c) 80°
(d) 90°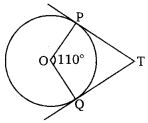

Solution: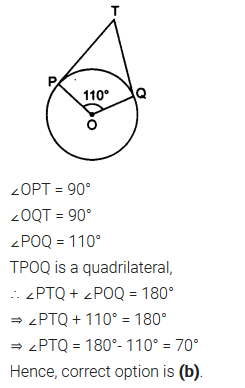

Download NCERT Solutions For Class 10 Maths Chapter 10 Circles PDF

Ex 10.2 Class 10 Maths Question 3.
If tangents PA and PB from a point P to a circle with centre O are inclined to each other at angle of 80°, then ∠POA is equal to
(a) 50°
(b) 60°
(c) 70°
(d) 80°
Solution: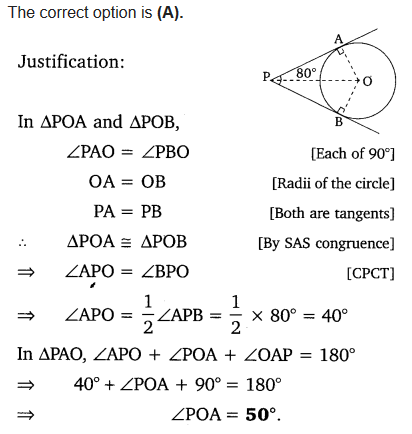

Ex 10.2 Class 10 Maths Question 4.
Prove that the tangents drawn at the ends of a diameter of a circle are parallel.
Solution: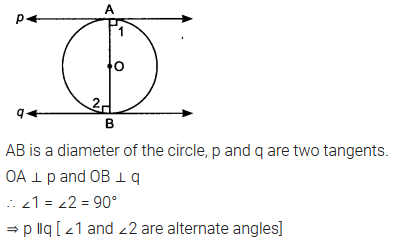

Ex 10.2 Class 10 Maths Question 5.
Prove that the perpendicular at the point of contact to the tangent to a circle passes through the centre.
Solution: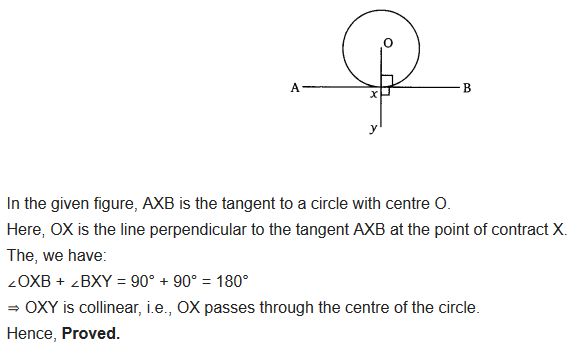

Ex 10.2 Class 10 Maths Question 6.
The length of a tangent from a point A at distance 5 cm from the centre of the circle is 4 cm. Find the radius of the circle.
Solution: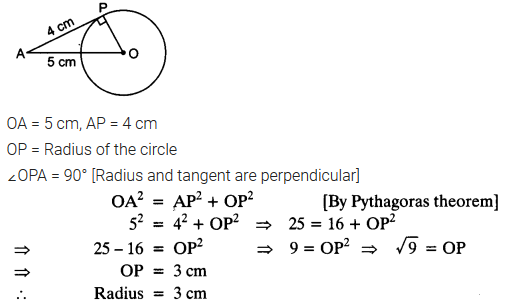

Ex 10.2 Class 10 Maths Question 7.
Two concentric circles are of radii 5 cm and 3 cm. Find the length of the chord of the larger circle which touches the smaller circle.
Solution: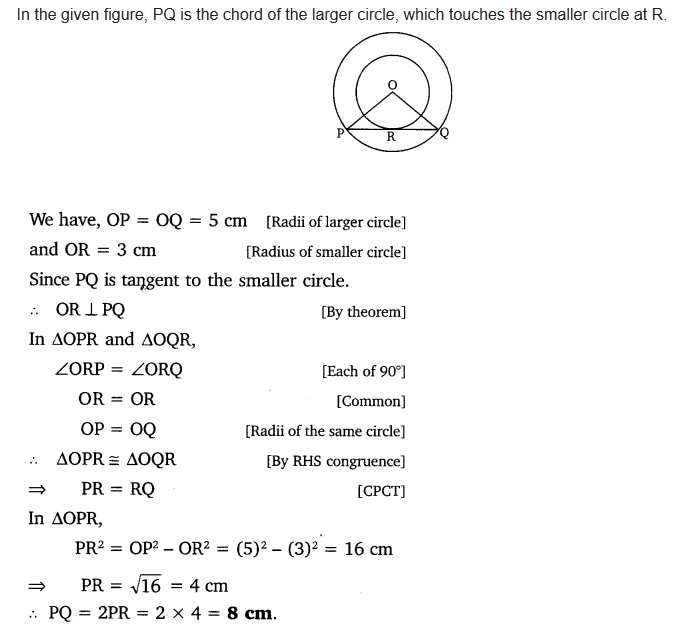

Ex 10.2 Class 10 Maths Question 8.
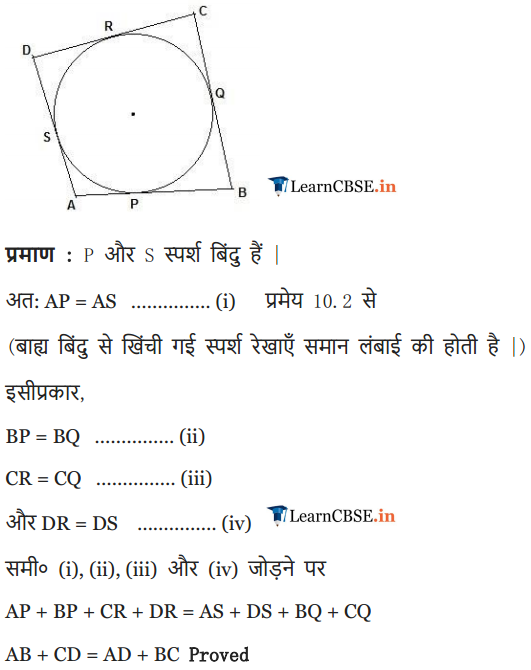
A quadrilateral ABCD is drawn to circumscribe a circle (see figure). Prove that AB + CD = AD + BC.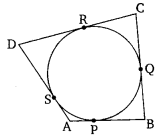

Solution: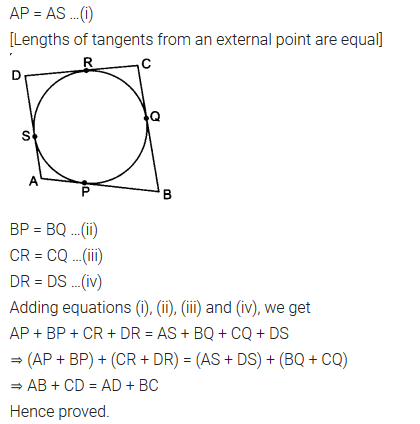

Ex 10.2 Class 10 Maths Question 9.
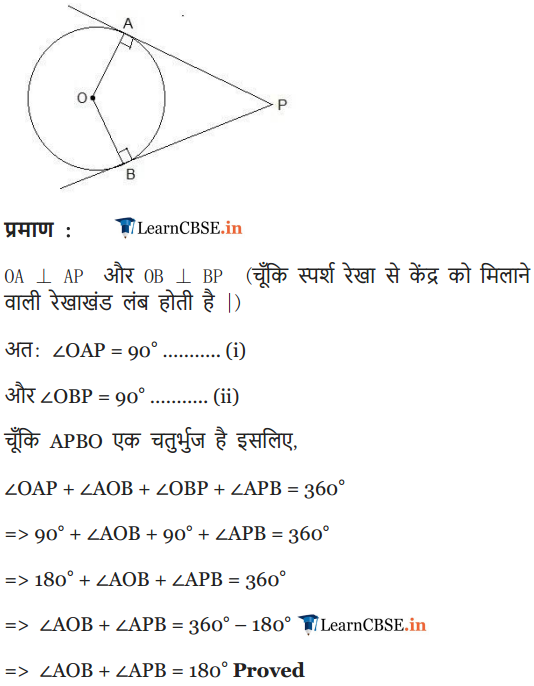
In figure, XY and X’Y’ are two parallel tangents to a circle , x with centre O and another tangent AB with point of contact C intersecting XY at A and X’Y’ at B. Prove that ∠AOB = 90°.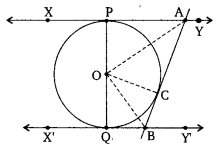

Solution:

Ex 10.2 Class 10 Maths Question 10.
Prove that the angle between the two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line segment joining the points of contact at the centre.
Solution: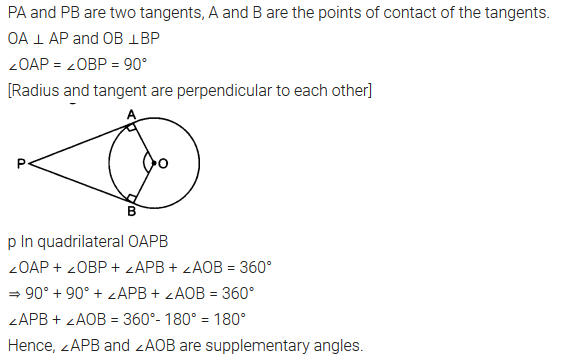

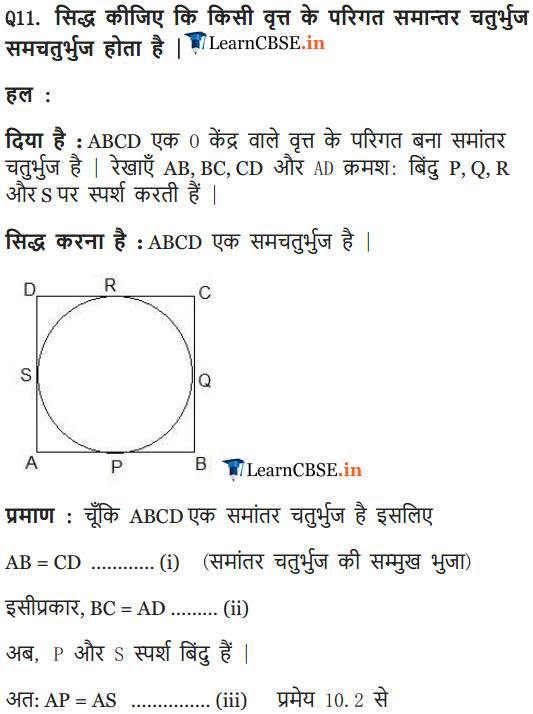
Ex 10.2 Class 10 Maths Question 11.
Prove that the parallelogram circumscribing a circle is a rhombus.
Solution: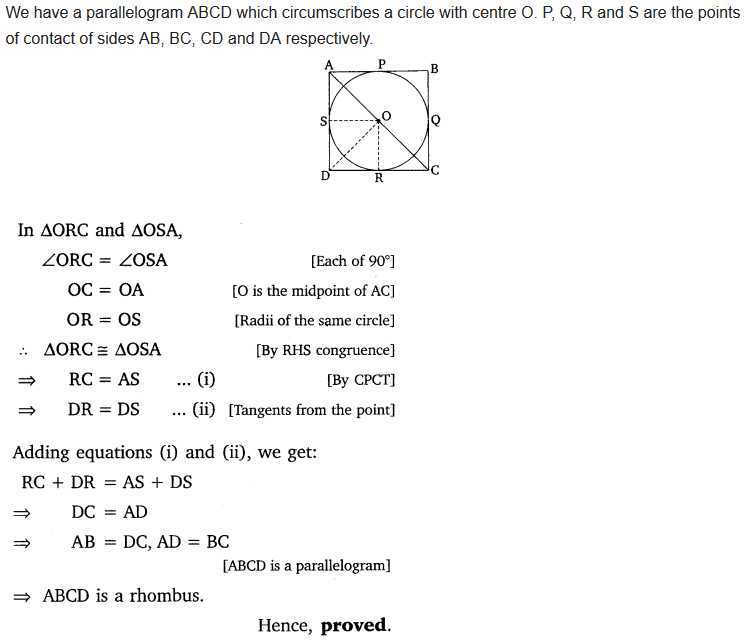

Ex 10.2 Class 10 Maths Question 12.
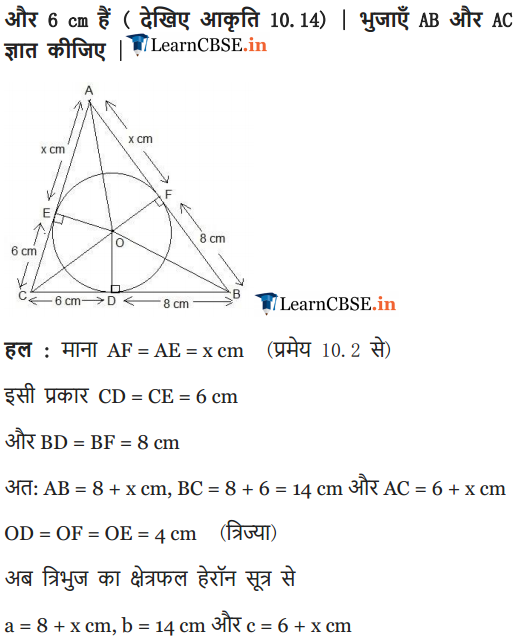
A triangle ABC is drawn to circumscribe a circle of radius 4 cm such that the segments BD and DC into which BC is divided by the point of contact D are of lengths 8 cm and 6 cm respectively (see figure). Find the sides AB and AC.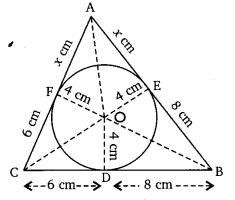

Solution: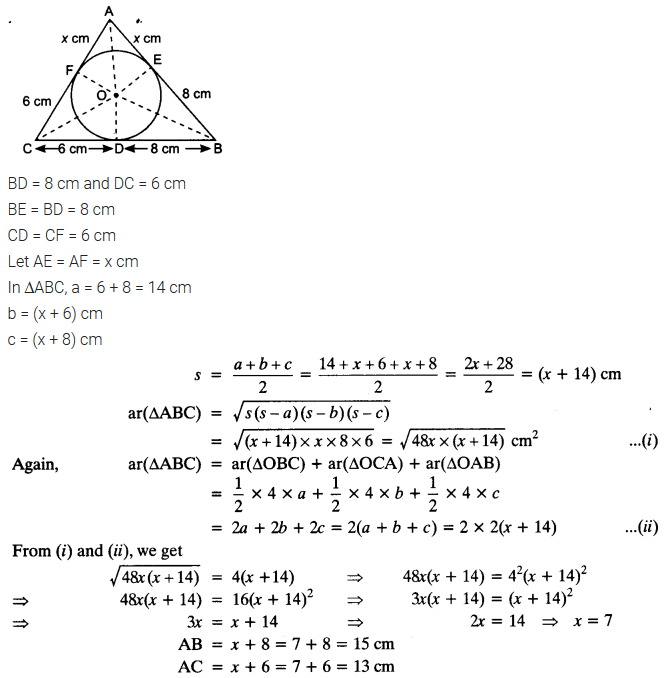

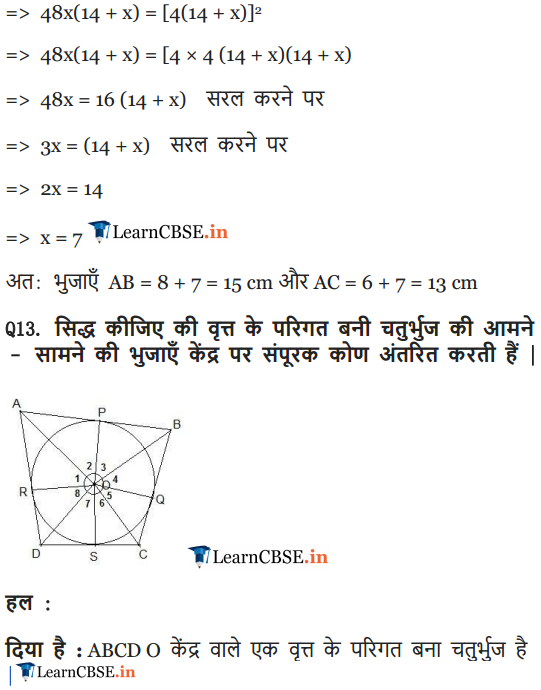
Ex 10.2 Class 10 Maths Question 13.
Prove that opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the centre of the circle.
Solution: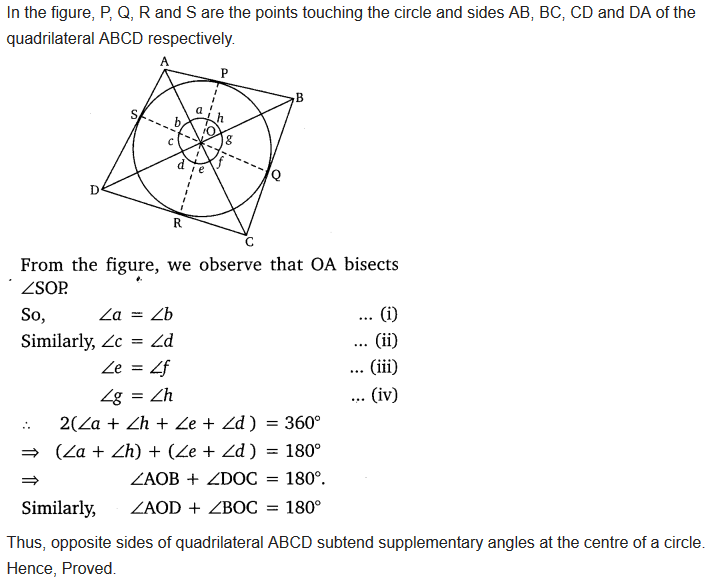

NCERT Solutions for Class 10 Maths Chapter 10 Circles (Hindi Medium) Ex 10.2

Extra Questions for Class 10 Maths Circles with Answers

Circles Class 10 Extra Questions Very Short Answer Type

Question 1.
In fig., QR is a common tangent to the given circles, touching externally at the point T. The tangent at T meet QR at P. If PT = 3.8 cm, find the length of QR.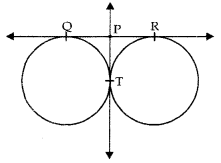

Answer:
Length of tangents drawn from external point to a circle are equal.
∴ QP = PT and PR = PT
QP = 3.8 cm and PR = 3.8 cm
Now, QR = QP + PR = 3.8 + 3.8 = 7.6 cm

Question 2.
From an external point P, tangents PA and PB are drawn to a circle with centre O. If ∠PAB = 50°, then find ∠AOB. [CBSE 2016]
Answer:
∵ PA and PB are tangents to the given circle.
∴ ∠PAO = 90° (Radius is perpendicular to the tangent at the point of contact O.)
Now, ∠PAB = 50° (Given)
∴ ∠OAB = ∠PAO – ∠PAB
= 90° – 50° = 40°
In ∆ OAB OB = OA (Radii of the circle)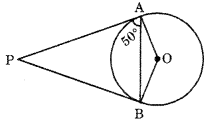

∴ ∠OAB = ∠OBA = 40°
(Angles opposite to equal sides are equal)
Now, ∠AOB + ∠OAB + ∠OBA = 180° (Angle sum property)
⇒ ∠AOB = 180° – (40° + 40°) = 100°

Question 3.
In figure, PQ is a tangent at a point C to a circle with centre O. If AB is a diameter and ∠CAB = 30°, find ∠PCA. [CBSE Outside Delhi 2016]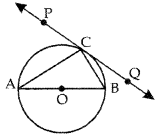

Answer:
Join OC, OA = OC [radii of same circle]
⇒ ∠ACO = ∠CAO = 30°
and ∠OCP = 90°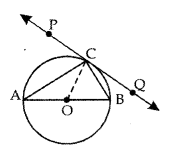

[tangent ⊥ radius at point of contact]
⇒ ∠PCA = ∠OCP – ∠AC)
= 90° – 30° = 60°

Question 4.
In fig., if AD = 15 cm, CF = 12 cm and BE = 7 cm, then find the perimeter of the triangle ABC.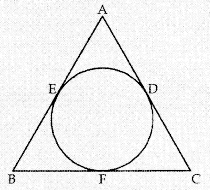

Answer:
Since, the lengths of two tangents drawn from an external point to a circle are equal.
∴ AD = AE = 15 cm, BE = BF = 7 cm,
CF = CD = 12 cm
Perimeter of ∆ABC
= AB + BC + CA
= (AE + BE) + (BF + CF) + (CD + DA)
= {(15 + 7) + (7 +12) + (12 + 15)} cm
= (22 + 19 + 27) cm = 68 cm.

Question 5.
In fig., PT1 and PT2 are tangents to the circle drawn from an external point P. CD is a third tangent touching circle at Q. If PT2 = 12 cm and CQ = 2 cm. What is the length of PC?
Answer:
Length of tangents drawn from external point are equal.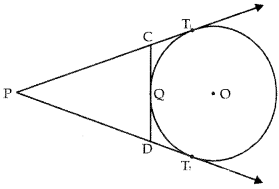

Therefore, PT1 = PT2 = 12 cm
CQ = CT1 = 2 cm
Now, PC = PT1 – CT1 = (12 – 2) cm = 10 cm

Question 6.
Two tangents are drawn to a circle from an external point P, touching the circle at the points A and B and a third tangent intersects segment PA in C and segment PB in D and touches the circle at Q. If PA = 20 units, then find the perimeter of ∆PCD.
Answer:
Since, the length of tangents drawn from an external point of a circle are equal.
∴ PA = PB, CA = CQ and DB = DQ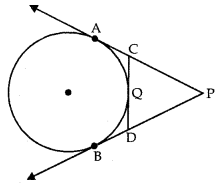

Now, perimeter of ∆PCD = PC + CD + DP
= PC + (CQ + QD) + DP
= PC + (CA + DB) + PD [∵ CQ = CA and DQ = DB]
= (PC + CA) + (PD + DB)
= PA + PB
= PA + PA [∵ PB = PA]
= 2 PA = 2 × 20 = 40 units.
Hence, the perimeter of ∆PCD is 40 units.

Question 7.
PQ and PR are two tangents drawn from the point P to the circle whose centre is at O. If ∠QOR = 260°, then find ∠QPR.
Answer: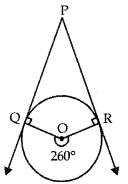

Clearly, ∠QOR of quad. PQOR is 360° – 260° = 100° and since angle between two tangents drawn from an external point to a circle are supplementary to the angle subtended by the line segments joining the point of contact at the centre.
∴ ∠QPR = 180° – 100° = 80°

Question 8.
In fig., PQ and PR are tangents drawn from P. If ∠QPR = 40°, then find ∠QSR.
Answer:
We know that, ∠QOR and ∠QPR are supplementary,
⇒ ∠QOR + ∠QPR = 180°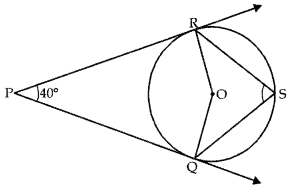

= 180° – 40° = 140°
Also we know that angle subtended at the centre is twice the angle subtended at the circumference.
∴ ∠QOR = 2 ∠QSR
⇒ ∠QSR = 12 ∠QOR = 12 × 140° = 70°

Circles Class 10 Extra Questions Short Answer Type-1

Question 1.
In the given figure, PA and PB are tangents to the circle from an external point P. CD is another tangent touching the circle at Q. If PA = 12 cm, QC = QD = 3 cm, then find PC + PD. [CBSE 2017]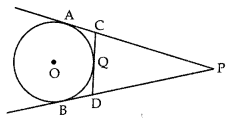

Answer:
PA = PC + CA = PC + CQ
[∵ Length of tangents drawn from external point to circle are equal ⇒ CA = CQ]
⇒ 12 = PC + 3
⇒ PC = 9 cm
⇒ Similarly, PD= 9 cm
∴ PC + PD = 18 cm

Question 2.
In the figure, AB and CD are common tangents to two circles of unequal radii. Prove that AB = CD. [CBSE Delhi 2017]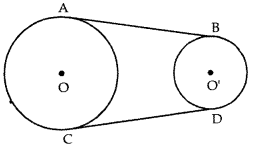

Answer:
Construction: Extend AB and CD to meet at P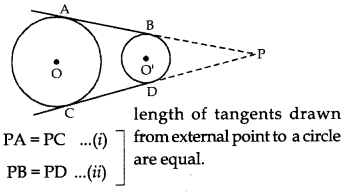

(i) – (ii) ⇒ PA – PB = PC – PD
⇒ AB = CD
Proved

Question 3.
In figure, a circle is inscribed in a ∆ ABC, such that it touches the sides AB, BC and CA at points D, E and F respectively. If the lengths of sides AB, BC and CA are 12 cm, 8 cm and 10 cm respectively, find the lengths of AD, BE and CF. [CBSE 2016]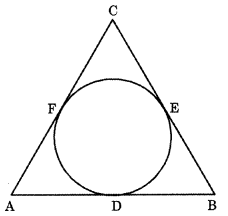

Answer:
AB = 12 cm
⇒ AD + BD = 12 cm …(1)
BC = 8 cm
⇒ BE + CE = 8 cm …(2)
CA = 10 cm
⇒ AF + CF = 10 cm …………. (3)
CF = CE ………… (4)
[Tangents drawn from external point to circle are equal]
Similarly
AF = AD …………. (5)
Also BD = BE ……………. (6)
Using (4) and (2), we get
BE + CF = 8 cm ………… (7)
Using (5) and (3), we get
AD + CF = 10 cm ……………. (8)
Using (6) and (1), we get
AD + BE = 12 cm …………….. (9)
Adding (7), (8) and (9), we get
BE + CF + AD + CF + AD + BE = 8cm + 10cm + 12cm
⇒ 2AD + 2BE + 2CF = 30 cm
⇒ 2(AD + BE + CF) = 30 cm
⇒ AD + BE + CF = 15 cm …….. (10)
Subtracting (7) from (10), we get
AD + BE + CF – BE – CF = 15 cm – 8 cm
⇒ AD = 7 cm
Subtracting (8) from (10), we get
AD + BE + CF – AD – CF = 15 cm – 10 cm
⇒ BE = 5 cm
Subtracting (9) from (10), we get
AD + BE + CF – AD – BE = 15 cm – 12 cm
⇒ CF = 3 cm
Thus, the lengths of AD, BE and CF are 7 cm, 5 cm and 3 cm, respectively.

Question 4.
In figure, a quadrilateral ABCD is drawn to circumscribe a circle, with centre O, in such a way that the sides AB, BC, CD and DA touch the circle at the points P, Q, R and S respectively. Prove that AB + CD = BC + DA. [A.I.2017, CBSE Outside Delhi 2016]
Answer:
As tangents drawn from external point are equal
∴ AP = AS, BP = BQ, CR = CQ, DR = DS
∴ AB + CD = AP + PB + CR + DR
⇒ AB + CD = AS + BQ + CQ + DS
= (AS + SD) + (BQ + CQ) = AD + BC

Question 5.
If PS and PT are tangents from an external point P such that PS = 10 cm and ∠SPT = 60°. Find the length of chord ST.
Answer:
As tangents from external point are equal in length.
∴ PT = PS
⇒ APST is isosceles A.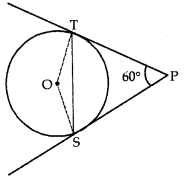

⇒ ∠PTS = ∠PST = (180∘−60∘)2 = 60°
⇒ ∆PST is equilateral.
∴ PS = PT = ST
∴ ST = 10 cm.

Question 6.
In the given figure, O is the centre of the circle, PT is the tangent and PAB is the secant passing through centre O. If PT = 8 cm and PA = 4 cm, then find the radius of the circle.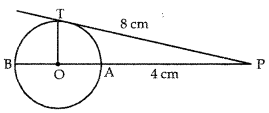

Answer:
Let x be the radius of circle.
⇒ OT = OA = X
PO = 4 + x
OT ⊥ PT
∆OTP is rt. ∠d at T.
∴ OP2 = OT2 + TP2
⇒ (4 + x)2 = x2 + 64
⇒ 16 + x2 + 8x = x2 + 64
⇒ 8x = 48
⇒ x = 6 cm.

Question 7.
ABC is a right triangle, right angled at B. A circle is inscribed in it. The lengths of the two sides containing the right angle are 6 cm and 8 cm. Find the radius of the incircle.
Answer:
Let ‘r’ be radius of the circle. Further, let D, E, F are the points where the incircle touches the sides AB, BC, CA respectively.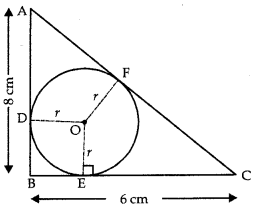

Then OD = OE = OF = r cm
Also, AB = 8 cm and BC = 6 cm
Since, the tangents to a circle from an external point are equal, we have
AF = AD = (8 – r) cm
and CF = CE = (6 – r) cm
∴ AC = AF + CF = (8 – r) + (6 – r)
= 14 – 2 r
Using Pythagoras Theorem
AC2 = AB2 + BC2
⇒ (14 – 2r)2 = 82 + 62 = 100
⇒ 14 – 2r = 10
⇒ 2r = 4
⇒ r = 2 cm
Hence, the radius of incircle is 2 cm.

Question 8.
A circle touches the side BC of a ∆ABC at P, and touches AB and AC produced at Q and R respectively as shown in fig. Show that AQ = 12 (Perimeter of ∆ABC).
Answer:
Since, lengths of tangents drawn from an external point to a circle are equal.
∴ AQ = AR ………… (i)
BP = BQ ………… (ii)
CP = CR …………. (iii)
Perimeter of ∆ABC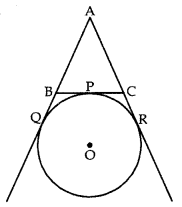

= AB + BC + CA
= AB + BP + PC + AC
= AB + BQ + CR + AC
(∵ of (ii) and (iii))
= AQ + AR = 2AQ (∵ of (i))
⇒ AQ = 12 (Perimeter of ∆ABC)

Question 9.
In fig. FA is a tangent from an external point P to a circle with centre O. If ∠POB = 115°, then find ∠APO.
Answer:
∵ ∠POA + ∠POB = 180° (Linear pair)
∴ ∠POA = 180° – 115° = 65°
Since, the tangent at any point of a circle is perpendicular to the radius through the point of contact.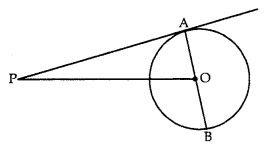

∴ ∠PAB = 90°
Now, in ∆APO,
∠APO + ∠PAO + ∠POA = 180°
or ∠APO + 90° + 65° = 180° (Sum of angles of ∆)
or ∠APO+ 155° = 180°
or ∠APO = 180° – 155° = 25°

Question 10.
In figure, AP and BP are tangents to a circle with centre O, such that AP = 5 cm and ∠APB = 60° Find the length of chord AB. [CBSE 2016]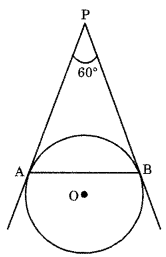

Answer:
As the lengths of the tangents drawn from an external point to a circle are equal.
∴ PA = PB
In ∆PAB, sides PA and PB are of the same length.
Hence, ∆PAB is isosceles, with PA = PB and ∠PAB = ∠PBA = x (say).
It is given that
∠APB = 60°
In ∆PAB
∠PAB + ∠PBA + ∠APB =180°
[Angle sum property of A]
∴ x + x + 60° = 180°
⇒ 2x = 120°
⇒ x = 60°
Thus, ∠PAB = ∠PBA = ∠APB = 60°
⇒ ∆PAB is equilateral with AP = BP = AB
It is given that AP = 5 cm
∴ AB = AP = 5 cm
Thus, the length of the chord AB is 5 cm.

Question 11.
In figure, from an external point P, two tangents PT and PS are drawn to a circle with centre O and radius r. If OP = 2r, show that ∠OTS = ∠OST = 30°. [CBSE Outside Delhi 2016]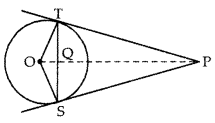

Answer:
In ∆OTP
∠OTP = 90° [radius 1 tangent]
Let ∠OPT = ∠OPS = θ
sin θ = OTOP=r2r=12
⇒ θ = 30°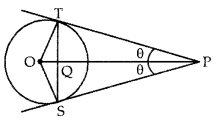

In ∆OTP using angle sum formula for ∆
∠POT = 180° – (∠OTP + θ)
= 180° – (90° + 30°) = 60°
Similarly, ∠POS = 60°
⇒ ∠SOT = 60° + 60° = 120°
Also, in ∆OTS OT = OS = r
⇒ ∠OTQ = ∠ OSQ
⇒ ∠OTQ = ∠ OSQ = (180∘−120∘2) = 30°

Circles Class 10 Extra Questions Short Answer Type-2

Question 1.
Two tangents TP and TQ are drawn to a circle with centre O from an external point T. Prove that ∠PTQ = 2∠OPQ. [CBSE Delhi 2017]
Answer:
Given: TP, TQ are tangents to circle C(o, r) at P and Q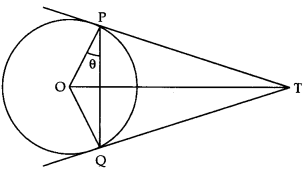

To prove: ∠PTQ = 2∠OPQ
Proof: Let ∠OPQ = θ
∠TPO = 90° [∵ Radius X Tangent]
⇒ ∠TPQ = ∠TPO-∠QPO = 90° – θ
Similarly ∠TQP = 90° – 0
But in ∆TPQ
∠TPQ + ∠TQP + ∠PTQ = 180° [Angle sum property]
90° – θ + 90° – θ + ∠PTQ = 180°
⇒ ∠PTQ = 2θ
⇒ = 2∠OPQ
Proved

Question 2.
Prove that the line segment joining the points of contact of two parallel tangents of a circle passes through its centre.
Answer: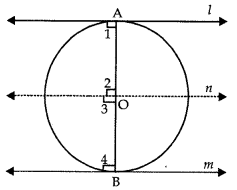

Given: l and m are two parallel tangents to the circle of centre ‘O’ at points A and B respectively.
To prove: AB is a diameter of circle i.e., AOB is a straight line.
Construction: Draw a line ‘n’ through O such that, l || n || m.
Proof: Now, l|| n and AB is a transversal.
∴ ∠1 + ∠2 = 180° [Co-interior angles are supplementary] ……. (i)
But ∠1 = 90°
[Radius OA ⊥ tangent ‘l’] …….. (ii)
(i) and (ii)
⇒ 90° + ∠2 = 180°
⇒ ∠2 = 180° – 90° = 90° …….. (iii)
Similarly, m||n and AB is a transversal.
∠3 + ∠4 = 180° … (iv)
But ∠4 = 90°
[Radius OB ⊥ tangent ‘m’] ……… (v)
(iv) and (v)
⇒ ∠3 + 90° = 180°
⇒ ∠3 = 180° – 90° = 90° …….. (vi)
Now ∠AOB = ∠2 + ∠3 = 90° + 90° = 180°
[Using (iii) and (vi)]
∴ AOB is a straight line.
Hence, AB is diameter of circle.
So, line segment joining the point of contact of two parallel tangents of a circle passes through its centre.

Question 3.
If from an external point P of a circle with centre O two tangents PQ and PR are drawn such that ∠QPR = 120°. Prove that 2PQ = PO.
Answer:
In ∆POQ and ∆POR.
∠1 = ∠2 = 90°
[90° = Angle between tangent and radius]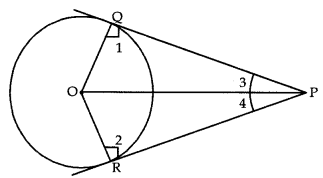

PO = OP (Common)
PQ = PR (Tangents drawn from external point are equal)
∴ ∆POQ ≅ ∆POR (By RHS)
⇒ ∠3 = ∠4 = 12 ∠QPR

Question 4.
ABC is a right-angled triangle, right angled at B and with BC = 6 cm and AB = 8 cm. A circle with centre O and radius x has been described in AABC. Find the values of x.
Answer:
We know that radius is perpendicular to tangent.
PO ⊥ BC and OQ ⊥ AB
∴ OPBQ is a rectangle.
But OP = OQ = x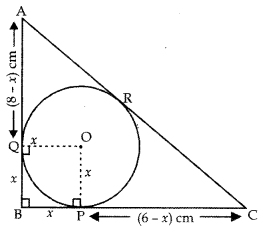

OPBQ is a square
Now, BP = x
∴ PC = (6 – x) cm
∴ OP = QB = x
∴ AQ (8 – x) cm
and PC = CR = (6 – x) cm
Now, AC = AB2+BC2−−−−−−−−−√
(By Pythagoras Theorem)
= 82+62−−−−−−√ = 642+362−−−−−−−−√ = √100
= 10 cm
AC = AR + CR
10 = (8 – x) + (6 – x)
10 = 14 – 2x
2x = 4cm
x = 2 cm

Question 5.
In the given figure ‘O’ is the centre of the circle. Determine ∠AQB and ∠AMB, if PA and PB are tangents and, ∠APB = 75°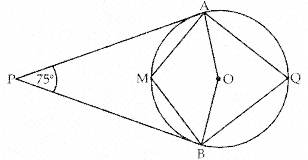

Answer:
Given: ∠APB = 75°, PA and PB are tangents.
To find: ∠AQB and ∠AMB
Proof: ∠AOB = 180° – 75° = 105° [∵ ∠P + ∠AOB = 180°]
∴ Reflex ∠AOB = 360° -105° = 255°
∴ ∠AQB = 12 ∠AOB = 12 x 255°
= 1271∘2

Question 6.
In the figure, quadrilateral ABCD circumscribes the circle. Find the length of the side CD.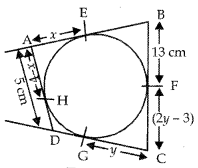

Answer:
AE = AH
[Length of tangents from external points]
x = 4 – x
⇒ 2x = 4
⇒ x = 2
DH = (5 – 2) = 3 cm
DH = DG = 3 cm
CF = CG
⇒ 2y – 3 = y
⇒ y = 3
∴ DC = DG + GC = 3 + 3 = 6 cm.

Circles Class 10 Extra Questions Long Answer Type 1

Question 1.
Prove that lengths of tangents drawn from an external point to a circle are equal. [CBSE 2017, 18]
Answer:
Given: A circle C(o, r), PA & PB are tangents drawn from external point P to the circle.
To prove: PA = PB
Construction: Join OA, OB & OP
Proof: Since radius ⊥ tangent at the point of contact.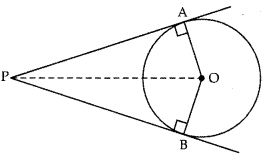

⇒ ∠PAO = ∠PBO ……………. (i)
In ∆OAP & ∆OBP
OA = OB
OP = OP
∠PAO = ∠PBO
⇒ ∆OAP ≅ ∆OBP
⇒ PA = PB [Hence Proved] c.p.c.t.

Question 2.
Prove that the lengths of tangents drawn from an external point to a circle are equal. [CBSE 2016]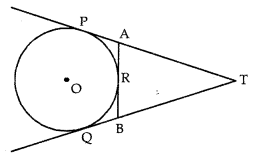

Using the above, do the following:
In figure TP and TQ are tangents from T to the circle with centre O and R is any point on the circle. If AB is tangent to the circle at R, prove that TA + AR = TB + BR.
Answer:
Refer Theorem II in Synopsis for first part.
Next,
TP = TQ [∵ Theorem II]
⇒ TA + AP = TB + BQ ………. (i)
But AP = AR ………………. (ii) [AP, AR are tangents drawn from external point A]
Similarly, BQ = BR ……………. (iii)
Putting for AP and BQ in (i) from (ii) and (iii) we get
TA + AR = TB + BR (Proved)

Question 3.
The centre of a circle of radius 13 cm is the point C (3, 6) and P (7, 9). is a point inside the circle. APB is a chord of the circle such that AP = PB. Calculate the length of AB.
Answer:
Given that AC = 13 cm.
Also, C (3, 6) and P (7,9)
∴ CP = (7−3)2+(9−6)2−−−−−−−−−−−−−−−√ (Distance formula)
= 16+9−−−−−√ = √25 = 5 cm

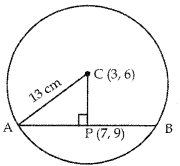
Also, CP ⊥ APB
∴ In right angled ∆CPA,
AC2 = AP2 + CP2 [By Pythagoras Theorem]
or (13)2 = AP2 + (5)2
or AP2 = 169 – 25 = 144
or AP2 = (12)2
or AP = 12
But AP = PB …………….. (Given)
⇒ AB = 2AP = 2 (12) cm = 24 cm.

Question 4.
AB and CD are two parallels of a circle such that AB = 10 cm and CD = 24 cm. If the chords are on the opposite sides of the centre and the distances between them is 17 cm, find the radius of the circle.
Answer:
Let radius of the circle be r cm.
Draw OE ⊥ CD and OF ⊥ AB.
Join OB and OD.
Also, OF = xcm
OE = (17 – x) cm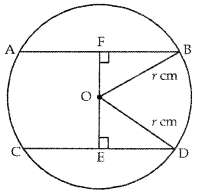

AB = 10 cm (Given)
∴ FB = 12 AB = 12 × 10 = 5 cm
Similarly, ED = 12 CD = 12 (24) = 12 cm
In right angled ∆OFB,
OB2 = OF2 + FB2
r2 = x2 + (5)2
r2 = x2 + 25 ……………. (1)
Also, in right angled AOED,
OD2 = OE2 + ED2
r2 = (17 – x)2 + (12)2
r2 = 289 + x2 – 34x + 144
r2 = x2 – 34x + 433 ……………… (2)
From (1) and (2), we get
x2 + 25 = x2 – 34x + 433
34x = 408
x = 40834 = 12
Putting the value of x in (1), we get
r2 = (12)2 + 25 = 144 + 25 = (13)2
r = 13 cm
Hence, radius of the circle is 13 cm.

Question 5.
Two circles of radii 10 cm and 8 cm intersect and the length of the common chord is 12 cm. Find the distance between their centres.
Answer:
Two circles having centre O and O’ and OA = 10 cm; O’A = 8 cm respectively.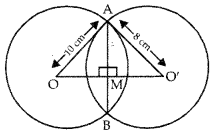

Also, AB = 12 cm be the length of common chord.
∴ AM = 12 = 12 (12) = 6 cm
In right angled ∆OMA,
OA2 = OM2 + AM2
(10)2 = OM2 + (6)2
or OM2 = 100 – 36
or OM2 = 64 = (8)2
or OM = 8 cm
Now, in right ∆ O’MA,
O’A2 = O’M2 + AM2
(8)2 = O’M2 + (6)2
or O’M2 = 64 – 36 = 28
or O’M = √28 = 5.29 cm.
∴ Required, distance between the centres
= OO’ = OM + MO’
= (8 + 5.29) cm
= 13.29 cm.

Question 6.
In the given figure, AB is the chord of a circle with centre O. AB is produced to C such that BC = OB. CO is joined and produced to meet the circle in D. If ∠ACD = y° and ∠AOD = x°, prove that x° = 3y°.
Answer: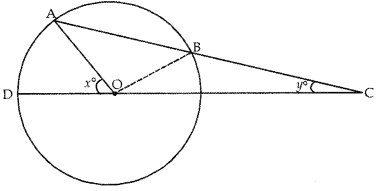

Given that,
BC = OB
⇒ ∠OCB = ∠BOC = y°.
In ∆OBC,
Exterior ∠OBA = ∠BOC +∠OCB
= y° + y° = 2y°
Now, OA = OB (Radii of same circle)
⇒ ∠OAB = ∠OBA = 2y°
In ∆AOC,
Exterior ∠AOD = ∠OAC + ∠OCA
= 2y° + y° = 3y°
But, ∠AOD = x° (Given that)
∴ x° = 3y°

Question 7.
In figure, two equal circles, with centres O and O’, touch each other at X. OO’ produced meets the circle with centre O’ at A. AC is tangent to the circle with centre O, at the point C. O’D is perpendicular to AC. Find the value of 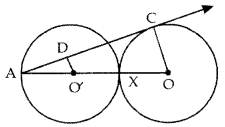DO′CO. [CBSE Outside Delhi 2016]

Answer:
Given: Two circles C(O’, r) and C(O, r).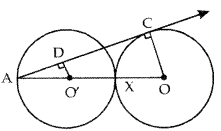

AX is diameter of C(O’, r) and AC is tangent to C (O, r).O’D ⊥ AC
To find: DO′CO
In ∆AO’D and ∆AOC
∠A = ∠A [Common angle]
∠ADO’ = ∠ACO [90° each]
⇒ ∆AO’D ~ ∆AOC
⇒ DO′CO=ADAC=AO′AO ……………. (1)
But AO’ = r
AO = AO’ + O’X + XO
= r + r + r = 3r
(1) ⇒ DO′CO=203=r3r=13
∴ DO′CO=13

Question 8.
In figure, O is the centre of a circle of radius 5 cm. T is a point such that OT = 13 cm and OT intersects circle at E. If AB is a tangent to the circle at E, find the length of AB, where TP and TQ are two tangents to the circle. [CBSE 2016]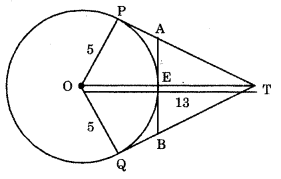

Answer:
From the given figure, we have TP = TQ
[∴ Tangents, drawn form an external point to a circle, have equal length.]
and ∠TQO = ∠TPO = 90°
[∵ Tangent to a circle is perpendicular to the radius through the point of contact]
In ∆ TOQ,
QT2 + OQ2 = OT2
⇒ QT2 = 132 – 52 = 144
⇒ QT = 12 cm
Now, OT – OE = ET
= 13 – 5 = 8 cm
Let QB = x cm
∴ QB = EB = x
[∵ Tangents, drawn from an external point to a circle, have equal length.]
Also, ∠OEB = 90°
[Tangent to a circle is perpendicular to the radius through the point of contact.]
In ∆TEB EB2 + ET2 = TB2
⇒ x2 + 82 = (12 – x)2
⇒ x2 + 64 = 144 + x2 – 24x
⇒ 24x = 80
⇒ x = 8024=103
AB = 2x = cm
∴ Thus, the length of AB is 203 cm.

Circles Class 10 Extra Questions HOTS

Question 1.
Let A be one point of intersection of two intersecting circles with centres O and Q. The tangents at A to the two circles meet the circles again at B and C respectively. Let the point P be located so that AOPQ is a parallelogram. Prove that P is the circumcentre of the triangle ABC.
Answer:
AQ is the radius and AB is a tangent to the circle with centre Q.
⇒ AQ ⊥ AB
[Radius is perpendicular to tangent through the point of contact]
Again OPQA is a || gm.
⇒ AQ || OP
Now AQ || OP and AQ ⊥ AB
⇒ OP⊥ AB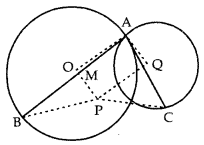

Let OP intersect AB at M
∴ OM ⊥ AB
∴ AM = BM
[∵ Perpendicular from the centre of a circle to a chord bisects the chord.]
∴ OM and hence OP is perpendicular bisector of AB.
Similarly, we can show that PQ is perpendicular bisector of AC.
Now in ∆ABC,
OP is the perpendicular bisector of side AB.
∴ PA = PB – [Any point on the perpendicular bisector of line segment is equidistant from the end points.]
Similarly, PA = PC
PA = PB = PC
⇒ P is equidistant from three vertices of ∆ABC.
⇒ The circle with P as centre and its distance from any vertex as radius passes through the three vertices of ∆ ABC and the point P is the circumcentre of the ∆ABC.

Question 2.
In the adj oining figure from an external point P, a tangent PT and a line segment PAB is drawn to a circle with centre O. ON is perpendicular on the chord AB. Prove that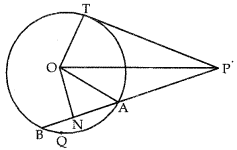

(i) PA.PB = PN2 – AN2
(ii) PN2 – AN2 = OP2 – OT2
(iii) PA.PB = PT2
Answer:
Observe that PA = PN – AN and PB = PN + BN
(i) ∴ PA. PB = (PN – AN) (PN + BN)
= (PN – AN) (PN + AN)
[AN = BN as perpendicular from centre bisects the chord]
= PN2 – AN2 ……………… (i)

(ii) In right ∆ONP,
OP2 = ON2 + NP2 ⇒ NP2
= OP2 – ON2 ………….. (a)
and in right 2ONA,
ON2 + AN2 = OA2 ………….. (b)
∴ PN2 – AN2 = (OP2 – ON2) – AN2 [using (a)]
= OP2 – (ON2 + AN2)
= OP2 – OA2 [using (b)] …………….. (ii)
= OP2 – OT2 [∵ OA = OT]

(iii) From (i) and (ii)
⇒ PA. PB = OP2 – OT2 = PT2
[in right ∠d ∆, OP2 = OT2 + PT2].

Question 3.
In the adjoining fig., AB is a line segment ’ and M is its mid-point. Semicircles are drawn with AM, MB and AB as diameters on the same side of line AB. A circle C(O, r) is drawn so that it touches all the three semicircles.
Prove that r = 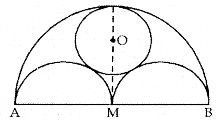16 AB.

Answer:
Let us mark ‘V and ‘N’ as mid-points of AM and MB. Join OL and ON.
Let AB = x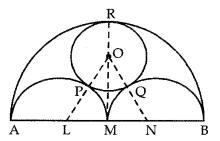

Note that O, P, L, are collinear and the points O, Q, N are collinear.
In rt. ∠d AOML
OL2 = OM2 + LM2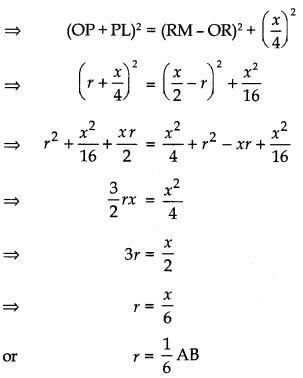

Question 4.
From point P outside the circle, with centre O, tangents PA and PB are drawn in the adjoining fig. If OP is equal to the diameter of the circle, prove that PAB is an equilateral triangle.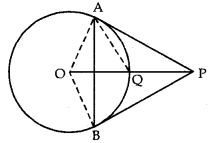

Answer:
Let us join OA, OB, AQ
Now, OP = 2OQ [∵ Diameter = 2 Radius]
⇒ OQ = PQ …….. (i)
or Q is mid-point of OP.
Also, OA ⊥ PA [Radius ⊥ tangent through the point of contact]
∆OAP is a right angled triangle.
Q is mid-point of hypotenuse OP.
⇒ QA = OQ = PQ
[As mid-point of hypotenuse of a right triangle is equidistant from three vertices] …… (ii)
But OQ = OA [Radii of same circle] ……. (iii)
(ii) and (iii)
⇒ OA = OQ = QA
⇒ ∆OAQ is an equilateral triangle.
⇒ ∠AOQ = 60°
But in ∆OAP,
∠APO + ∠OAP + ∠AOP = 180°
⇒∠APO + 90° + 60° = 180° [∴ ∠AOQ = ∠AOP = 60°]
⇒ ∠APO = 180° – 150° = 30°
Similarly we show that,
∠BPO = 30°
⇒ ∠APB = ∠APO + ∠BPO
= 30°+ 30° = 60° …(iv)
Aso in ∆APB,
PA = PB
[Tangents from external point P]
∠PAB = ∠PBA ………….. (v)
In ∆APB, using angle sum property of triangle.
∠PAB + ∠PBA + ∠APB = 180°
⇒ 2∠PAB + 60° = 180°
⇒ 2∠PAB = 180° – 60° = 120°
⇒ ∠PAB = 60° ………….. (vi)
(iv), (v) and (vi)
⇒ ∠APB = ∠PAB = ∠PBA = 60° each.
⇒ ∆PAB is an equilateral ∆.

Question 5.
Two circles with radii a and b touch each other externally. Let c be the radius of a circle which touches these two circles as well as a common tangent to the two circles, prove that: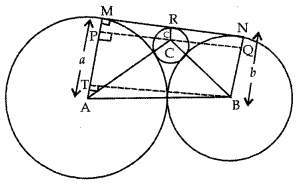
1c√=1a√+1b√

Answer:
Let us draw a line through centre C of smaller circle parallel to MN let it meet AM and BN at P and Q respectively. Join AC and BC. clearly ∠APC = 90° and ∠BQC = 90°
AP = AM – PM = a – c, AC = a + c
and BQ = BN – QN = b – c, BC = b + c
In right angled ∆APC,
PC = BC2−BQ2−−−−−−−−−√ = (b+c)2−(b−c)2−−−−−−−−−−−−−−√
= √4bc = 2√ac
Similarly, in right ∆BQC,
QC ⇒ BC2−BQ2−−−−−−−−−√ = (b+c)2−(b−c)2−−−−−−−−−−−−−−√
= √4bc = 2√bc
Also, draw BT || MN meeting AM at T.
Now, AB = a + b and AT = AM – MT = a – b
In right ∆ABT,
BT = AB2−AT2−−−−−−−−−√ = (a+b)2−(a−b)2−−−−−−−−−−−−−−−√
= √4ab = 2√ab
But BT = MN
⇒ MN = 2√ab
But MN = MR + RN = PC + QC
⇒ 2√ab = 2√ac + 2√bc
Dividing throughout by 2√abc, we get
1c√=1b√+1a√

Question 6.
In the given figure, AOC is a diameter of the circle. If AB = 7 cm, BC = 6 cm and CD = 2 cm, find the perimeter of cyclic quadrilateral ABCD.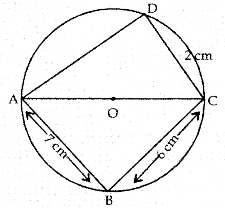

Answer:
AOC is a diameter of the circle.
∴ ∠ABC = 90° (Angle in semicircle)
So, in rt. angled ∆ ABC,
AC2 = AB2 + BC2
or AC2 = (7)2 + (6)2 = 49 + 36
or AC2 = 85 ……….. (1)
Similarly, ∠ADC = 90° (Angle in semicircle)
So, in right angled ∆ADC,
AC2 = AD2 + DC2
or 85 = AD2 + (2)2
or AD2 = 85 – 4 = 81
or AD2 = (9)2
or AD = 9 cm
Now, perimeter of cyclic quadrilateral ABCD
= AB + BC + CD + DA
= (7 + 6 + 2 + 9) cm
= 24 cm.

Question 7.
In ∆ABC, AB = 8 cm, BC = 6 cm, CA = 4 cm. With the vertices of triangle as centre, three circles are described, each touching the other two externally. Find the radii of each circle.
Answer:
Let x cm, y cm, z cm be the radii of circle I, II and III respectively as shown in the figure.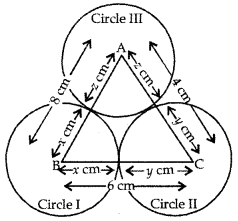

∴ x + y = 6 cm …(1)
y + z = 4 cm …(2)
z + x = 8 cm …(3)
Adding (1), (2), (3), we get
2 (x + y + z) = 18
x + y + z = 9 …(4)
(4) – (1) gives, z = 3
(4) – (2) gives, x = 5
(4) – (3) gives, y = 1
∴ Radii of circles are 5 cm, 1 cm and 3 cm.

Multiple Choice Questions

Choose the correct option for each of the following:

Question 1.
In fig., if the semiperimeter of ∆ ABC = 23 cm, then AF + BD + CE is: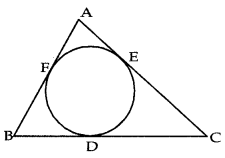

(a) 46 cm
(b) 11.5 cm
(c) 23 cm
(d) 34.5 cm
Answer:
(b) 11.5 cm

Question 2.
In fig., AP = 2 cm, BQ = 3 cm and RC = 4 cm, then the perimeter of ∆ ABC (in cm) is: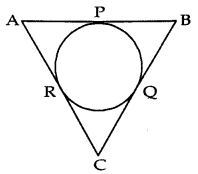

(a) 16
(b) 18
(c) 20
(d) 21
Answer:
(b) 18

Question 3.
In fig., two circles with centres A and B touch each other externally at point R.
The length of PQ (in cm) is: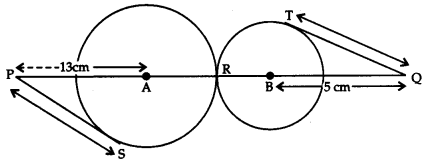

(a) 27
(b) 18
(c) 24
(d) 20
Answer:
(a) 27

Question 4.
In fig., two concentric circles with centre O are shown. AB and APQ are tangents to the inner circle from point A lying on the outer circle. If AB = 7.5 cm, then AQ is equal to: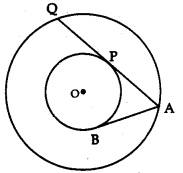

(a) 18 cm
(b) 15 cm
(c) 12 cm
(d) 10 cm
Answer:
(b) 15 cm

Question 5.
Quadrilateral ABCD circumscribes a circle as shown in fig. The side of quadrilateral which is equal to AP + BR is :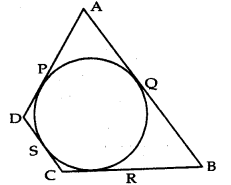

(a) AD
(b) BC
(c) AB
(d) BQ
Answer:
(c) AB

Question 6.
A tangent PT is drawn from an external point P to a circle of radius 3√2 cm such that distance of the point P from O is 6 cm as shown in fig. The value of ∠TPO is: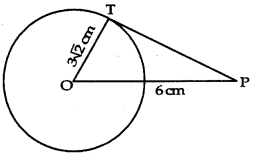

(a) 30°
(b) 45°
(c) 60°
(d) 75°
Answer:
(b) 45°

Question 7.
In fig., from an external point T, TP and TQ are two tangents to a circle with centre O so that ∠POQ = 110°, then ∠PTQ is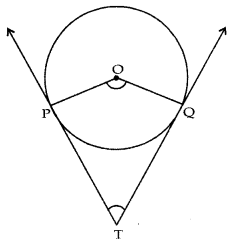

(a) 60°
(b) 70°
(c) 80°
(d) 90°
Answer:
(b) 70°

Question 8.
In fig., measure of ∠QSR is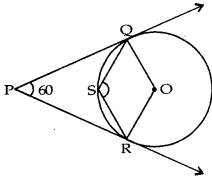

(a) 60°
(b) 100°
(c) 110°
(d) 120°
Answer:
(d) 120°

Question 9.
In fig., AB is a chord of the circle and AOC is its diameter such that ∠ACB = 50°. If AT is the tangent to the circle at the point A, then ∠BAT is equal to: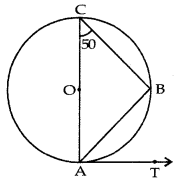

(a) 65°
(b) 60°
(c) 50°
(d) 40°
Answer:
(c) 50°

Question 10.
In fig., if O is the centre of a circle, PQ is a chord and the tangent PR at P makes an angle of 50° with PQ, then ∠POQ is equal to: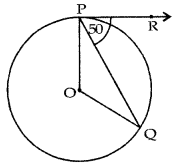

(a) 100°
(b) 80°
(c) 90°
(d) 75°
Answer:
(a) 100°

Question 11.
In fig., if PA and PB are tangents to the circle with centre O such that ∠APB = 50°, then ∠OAB is equal to: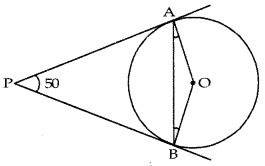

(a) 25°
(b) 30°
(c) 40°
(d) 50°
Answer:
(a) 25°

Question 12.
PQ and PT are tangents to a circle with centre O and radius 5 cm. If OP = 13 cm, then perimeter of quadrilateral PQOT is: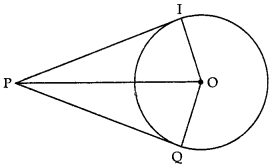

(a) 24 cm
(b) 34 cm
(c) 17 cm
(d) 20 cm
Answer:
(b) 34 cm

Question 13.
In fig., if OA = 5 cm and OM = 3 cm, the length of the chord AB (in cm) is: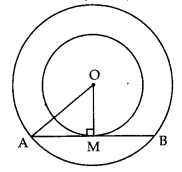

(a) 8
(b) 10
(c) 6
(d) 4
Answer:
(a) 8

Question 14.
In fig., AT is a tangent to the circle with centre O such that OT = 4 cm and ∠OTA = 30°. Then AT is equal to: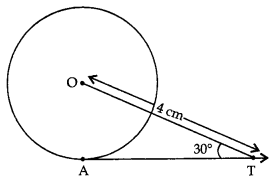

(a) 4 cm
(b) 2 cm
(c) 2√3 cm
(d) 4√3 cm
Answer:
(c) 2√3 cm

Question 15.
In fig., a quadrilateral ABCD is drawn to circumscribe a circle. Then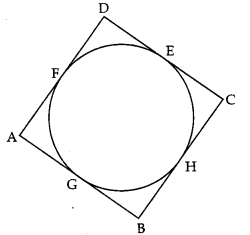

(a) AD + BC = AB + CD
(b) AB + BC = AD + CD
(c) BC + CD = AD + AB
(d) AB + BC + CD + AD = AC + BD
Answer:
(a) AD + BC = AB + CD

Fill in the Blanks

Question 1.
A line can intersect a circle at the most at _____________ points.
Answer:
two

Question 2.
A line intersecting the circle at two points is called a _____________ .
Answer:
secant

Question 3.
A line intersecting the circle exactly at one point is called a _____________ .
Answer:
tangent

Question 4.
Portion of secant intercepted by a circle is called _____________ of the circle.
Answer:
chord

Question 5.
The common point of tangent to a circle and the circle is called the _____________ .
Answer:
point of contact

Question 6.
Every point of the either in the interior or on the circle _____________ .
Answer:
chord

Question 7.
Every point of a to the circle except the point of _____________ lie outside the circle.
Answer:
tangent, contact

Question 8.
The tangent at any point of a circle is _____________ to the radius through the point of contact.
Answer:
perpendicular

Question 9.
A circle can have _____________ parallel tangents at the most whereas it can have parallel secants.
Answer:
two, infinite

Question 10.
We can draw no tangent from a point lying _____________ the circle.
Answer:
in the interior of

Important Questions for Class 10 Maths Chapter 10 Circles

Circles Class 10 Important Questions Very Short Answer (1 Mark)

Question 1.
In the given figure, O is the centre of a circle, AB is a chord and AT is the tangent at A. If ∠AOB = 100°, then calculate ∠BAT. (2011D)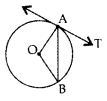

Solution: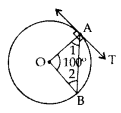

∠1 = ∠2
∠1 + ∠2 + 100° = 180°
∠1 + ∠1 = 80°
⇒ 2∠1 = 80°
⇒ ∠1 = 40°
∠1 + ∠BAT = 90°
∠BAT = 90° – 40° = 50°

Question 2.
In the given figure, PA and PB are tangents to the circle with centre O. If ∠APB = 60°, then calculate ∠OAB, (2011D)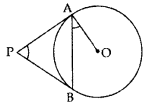

Solution: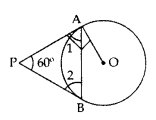

∠1 = ∠2
∠1 + ∠2 + ∠APB = 180°
∠1 + ∠1 + 60° = 180°
2∠1 = 180° – 60° = 120°
∠1 = 120∘2 = 60°
∠1 + ∠OAB = 90°
60° +∠OAB = 90°
∠OAB = 90° – 60° = 30°

Question 3.
In the given figure, O is the centre of a circle, PQ is a chord and PT is the tangent at P. If ∠POQ = 70°, then calculate ∠TPQuestion (2011OD)

Solution: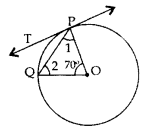

∠1 = ∠2
∠1 + ∠2 + 70° = 180°
∠1 + ∠1 = 180° – 70°
2∠1 = 110° ⇒ ∠1 = 55°
∠1 + ∠TPQ = 90°
55° + ∠TPQ = 90°
⇒ ∠TPQ = 90° – 55° = 35°

Question 4.
A chord of a circle of radius 10 cm subtends a right angle at its centre. Calculate the length of the chord (in cm). (2014OD)
Solution:
AB2 = OA2 + OB2 …[Pythagoras’ theorem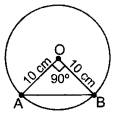

AB2 = 102 + 102
AB2 = 2(10)2
AB = 102–√ cm

Question 5.
In the given figure, PQ R is a tangent at a point C to a circle with centre O. If AB is a diameter and ∠CAB = 30°. Find ∠PCA. (2016OD)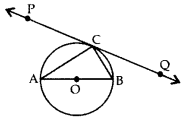

Solution:
∠ACB = 90° …[Angle in the semi-circle
In ∆ABC,
∠CAB + ∠ACB + ∠CBA = 180°
30 + 90° + ∠CBA = 180°
∠CBA = 180° – 30° – 90° = 60°
∠PCA = ∠CBA …[Angle in the alternate segment
∴ ∠PCA = 60°

Question 6.
In the given figure, AB and AC are tangents to the circle with centre o such that ∠BAC = 40°. Then calculate ∠BOC. (2011OD)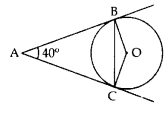

Solution: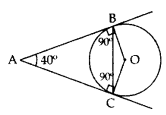

AB and AC are tangents
∴ ∠ABO = ∠ACO = 90°
In ABOC,
∠ABO + ∠ACO + ∠BAC + ∠BOC = 360°
90° + 90° + 40° + ∠BOC = 360°
∠BOC = 360 – 220° = 140°

Question 7.
In the given figure, a circle touches the side DF of AEDF at H and touches ED and EF produced at K&M respectively. If EK = 9 cm, calculate the perimeter of AEDF (in cm). (2012D)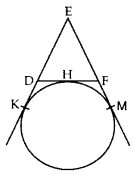

Solution:
Perimeter of ∆EDF
= 2(EK) = 2(9) = 18 cm

Question 8.
In the given figure, AP, AQ and BC are tangents to the circle. If AB = 5 cm, AC = 6 cm and BC = 4 cm, then calculate the length of AP (in cm). (2012OD)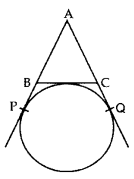

Solution:
2AP = Perimeter of ∆
2AP = 5 + 6 + 4 = 15 cm
AP = 152 = 7.5 cm

Question 9.
In the given figure, PA and PB are two tangents drawn from an external point P to a circle with centre C and radius 4 cm. If PA ⊥ PB, then find the length of each tangent. (2013D)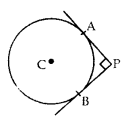

Solution: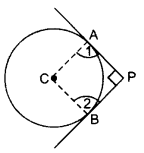

Construction: Join AC and BC.
Proof: ∠1 = ∠2 = 90° ….[Tangent is I to the radius (through the point of contact
∴ APBC is a square.
Length of each tangent
= AP = PB = 4 cm
= AC = radius = 4 cm

Question 10.
In the given figure, PQ and PR are two tangents to a circle with centre O. If ∠QPR = 46°, then calculate ∠QOR. (2014D)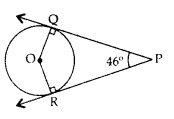

Solution:
∠OQP = 900
∠ORP = 90°
∠OQP + ∠QPR + ∠ORP + ∠QOR = 360° …[Angle sum property of a quad.
90° + 46° + 90° + ∠QOR = 360°
∠QOR = 360° – 90° – 46° – 90° = 134°

Question 11.
In the given figure, PA and PB are tangents to the circle with centre O such that ∠APB = 50°. Write the measure of ∠OAB. (2015D)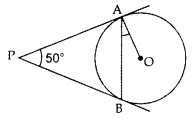

Solution:
PA = PB …[∵ Tangents drawn from external point are equal
∠OAP = ∠OBP = 90°
∠OAB = ∠OBA … [Angles opposite equal sides
∠OAP + ∠AOB + ∠OBP + ∠APB = 360° … [Quadratic rule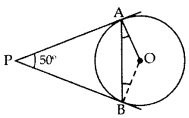

90° + ∠AOB + 90° + 50° = 360°
∠AOB = 360° – 230°
= 130°
∠AOB + ∠OAB + ∠OBA = 180° … [∆ rule
130° + 2∠OAB = 180° … [From (i)
2∠OAB = 50°
⇒ ∠OAB = 25°

Question 12.
From an external point P, tangents PA and PB are drawn to a circle with centre 0. If ∠PAB = 50°, then find ∠AOB. (2016D)
Solution:
PA = PB …[∵ Tangents drawn from external point are equal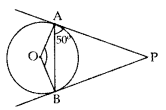

∠PBA = ∠PAB = 50° …[Angles equal to opposite sides
In ∆ABP, ∠PBA + ∠PAB + ∠APB = 180° …[Angle-sum-property of a ∆
50° + 50° + ∠APB = 180°
∠APB = 180° – 50° – 50° = 80°
In cyclic quadrilateral OAPB
∠AOB + ∠APB = 180° ……[Sum of opposite angles of a cyclic (quadrilateral is 180°
∠AOB + 80o = 180°
∠AOB = 180° – 80° = 100°

Question 13.
In the given figure, PQ is a chord of a circle with centre O and PT is a tangent. If ∠QPT = 60°, find ∠PRQ. (2015OD)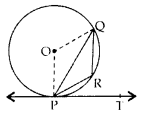

Solution:
PQ is the chord of the circle and PT is tangent.
∴ ∠OPT = 90° …[Tangent is I to the radius through the point of contact
Now ∠QPT = 60° … [Given
∠OPQ = ∠OPT – ∠QPT
⇒ ∠OPQ = 90° – 60° = 30°
In ∆OPQ, OP = OQ
∠OQP = ∠OPQ = 30° … [In a ∆, equal sides have equal ∠s opp. them
Now, ∠OQP + ∠OPQ + ∠POQ = 180°
∴ ∠POQ = 120° …[∠POQ = 180o – (30° + 30°)
⇒ Reflex ∠POQ = 360° – 120° = 240° …[We know that the angle subtended by an arc at the centre of a circle is twice the angle subtended by it at any point on the remaining part of the circle
∴ Reflex ∠POQ = 2∠PRO
⇒ 240° = 2∠PRQ
⇒ ∠PRQ = 240∘2 = 120°

Question 14.
In the given figure, the sides AB, BC and CA of a triangle ABC touch a circle at P, Q and R respectively. If PA = 4 cm, BP = 3 cm and AC = 11 cm, find the length of BC (in cm). (2012D)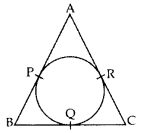

Solution: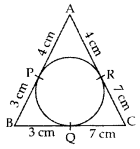

AP = AR = 4 cm
RC = 11 – 4 = 7 cm
RC = QC = 7 cm
BQ = BP = 3 cm
BC = BQ + QC
= 3 + 7 = 10 cm

Question 15.
In a right triangle ABC, right-angled at B, BC = 12 cm and AB = 5 cm. Calculate the radius of the circle inscribed in the triangle (in cm). (2014OD)
Solution: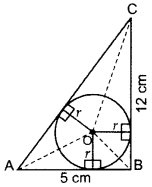

AC2 = AB2 + BC2 …[Pythagoras’ theorem
= (5)2 + (12)2
AC2 = 25 + 144
AC = 169−−−√ = 13 cm
Area of ∆ABC = Area of ∆AOB + ar. of ∆BOC + ar. of ∆AOC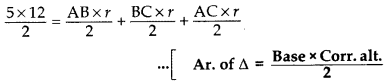

60 = r(AB + BC + AC)
60 = r(5 + 12 + 13)
60 = 30r ⇒ r = 2 cm

Question 16.
Find the perimeter (in cm) of a square circum scribing a circle of radius a cm. (2011OD)
Solution: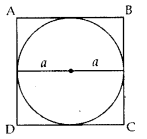

Radius = R
AB = a + a = 2a
∴ Perimeter = 4(AB)
= 4(2a)
= 8a cm

Question 17.
In the given figure, a circle is inscribed in a quadrilateral ABCD touching its sides AB, BC, CD and AD at P, Q, R and S respectively. If the radius DA of the circle is 10 cm, BC = 38 cm, PB = 27 cm and AD ⊥ CD, then calculate the length of CD. (2013OD)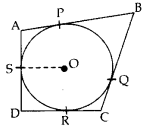

Solution:
Const. Join OR
Proof. ∠1 = ∠2 = 90° … [Tangent is ⊥ to the radius through the point of contact
∠3 = 90° …[Given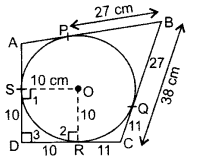

∴ ORDS is a square.
DR = OS = 10 cm …(i)
BP = BQ = 27 cm …[Tangents drawn from an external point
∴ CQ = 38 – 27 = 11 cm
RC = CO = 11 cm …[Tangents drawn from an external point
DC = DR + RC = 10 + 11 = 21 cm …[From (i) & (ii)

Circles Class 10 Important Questions Short Answer-I (2 Marks)

Question 18.
Prove that the tangents drawn at the ends of a diameter of a circle are parallel. (2012OD)
Solution: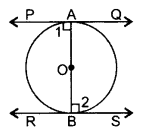

Proof: ∠1 = 90° …(i)
∠2 = 90° …(ii)
∠1 = ∠2 … [From (i) & (ii)
But these are alternate interior angles
∴PQ || RS

Question 19.
In the figure, AB is the diameter of a circle with centre O and AT is a tangent. If ∠AOQ = 58°, find ∠ATQ.  (2015D)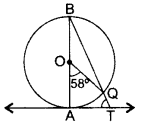

Solution:
∠ABQ = 12 ∠AOQ = 58∘2 = 29°
∠BAT = 90° ….[Tangent is ⊥ to the radius through the point of contact
∠ATQ = 180° – (∠ABQ + ∠BAT)
= 180 – (29 + 90) = 180° – 119° = 61°

Question 20.
Two concentric circles are of radii 7 cm and r cm respectively, where r > 7. A chord of the larger circle, of length 48 cm, touches the smaller circle. Find the value of r. (2011D)
Solution: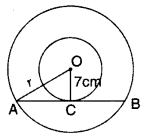

Given: OC = 7 cm, AB = 48 cm
To find: r = ?
∠OCA = 90° ..[Tangent is ⊥ to the radius through the point of contact
∴ OC ⊥ AB
AC = 12 (AB) … [⊥ from the centre bisects the chord
⇒ AC = 12 (48) = 24 cm
In rt. ∆OCA, OA2 = OC2 + AC2 … [Pythagoras’ theorem
r2 = (7)2 + (24)2
= 49 + 576 = 625
∴ r= 625−−−√ = 25 cm

Question 21.
In the figure, the chord AB of the larger of the two concentric circles, with centre O, touches the smaller circle at C. Prove that AC = CB. (2012D)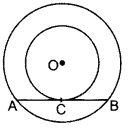

Solution: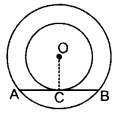

Const.: Join OC
Proof: AB is a tangent to smaller circle and OC is a radius.
∴ ∠OCB = 90° … above theorem
In the larger circle, AB is a chord and OC ⊥ AB.
∴ AC = CB … [⊥ from the centre bisects the chord

Question 22.
In the given figure, a circle touches all the four sides of a quadrilateral ABCD whose sides are AB = 6 cm, BC = 9 cm and CD = 8 cm. Find the length of side AD. (2011OD)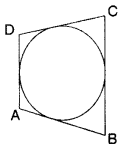

Solution:
AB + CD = AD + BC
6 + 8 = AD + 9
14 – 9 = AD ⇒ AD = 5 cm

Question 23.
Prove that the parallelogram circumscribing a circle is a rhombus. (2012D, 2013D)
Solution:
Given. ABCD is a ॥gm.
To prove. ABCD is a rhombus.
Proof. In ॥gm, opposite sides are equal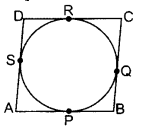

AB = CD
and AD = BC ..(i)
AP = AS …[Tangents drawn from an external point are equal in length
PB = BQ
CR = CO
DR = DS
By adding these tangents,
(AP + PB) + (CR + DR) = AS + BQ + CQ + DS
AB + CD = (AS + DS) + (BQ + CQ)
AB + CD = AD + BC
AB + AB = BC + BC … [From (i)
2AB = 2 BC
AB = BC …(ii)
From (i) and (ii), AB = BC = CD = DA
∴ ॥gm ABCD is a rhombus.

Question 24.
In figure, a quadrilateral ABCD is drawn to circum- DA scribe a circle, with centre O, in such a way that the sides AB, BC, CD and DA touch the circle at the points P, Q, RA and S respectively. Prove that: AB + CD = BC + DA. (2013 OD, 2016 OD)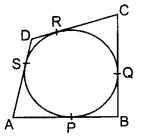

Solution: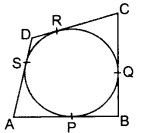

AP = AS ……(i) (Tangents drawn from an external point are equal in length
BP = BO …(ii)
CR = CQ ….(iii)
DR = DS ..(iv)
By adding (i) to (iv)
(AP + BP) + (CR + DR) = AS + BQ + CQ + DS
AB + CD = (BQ + CQ) + (AS + DS)
∴ AB + CD = BC + AD (Hence proved)

Question 25.
In the given figure, an isosceles ∆ABC, with AB = AC, circumscribes a circle. Prove that the point of contact P bisects the base BC. (2012D)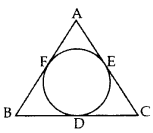

Solution:
Given: The incircle of ∆ABC touches the sides BC, CA and AB at D, E and F F respectively.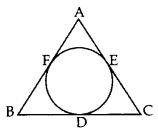

AB = AC
To prove: BD = CD
Proof: Since the lengths of tangents drawn from an external point to a circle are equal
∴ AF = AE … (i)
BF = BD …(ii)
CD = CE …(iii)
Adding (i), (ii) and (iii), we get
AF + BF + CD = AE + BD + CE
⇒ AB + CD = AC + BD
But AB = AC … [Given
∴ CD = BD

Question 26.
In Figure, a right triangle ABC, circumscribes a circle of radius r. If AB and BC are of lengths 8 cm and 6 cm respectively, find the value of r. (2012OD)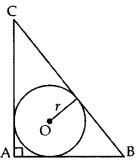

Solution:
Const.: Join AO, OB, CO
Proof: area of ∆ABC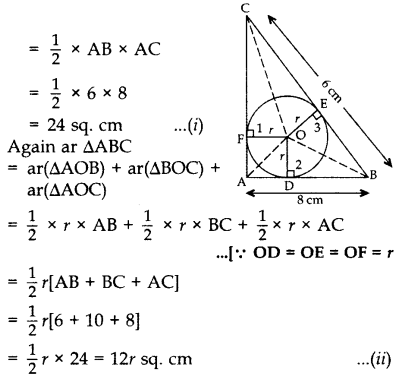

From (i) and (ii), we get 12r = 24
∴ r = 2 cm

Question 27.
In the given figure, a circle inscribed in ∆ABC touches its sides AB, BC and AC at points D, E & F K respectively. If AB = 12 cm, BC = 8 cm and AC = 10 cm, then find the lengths of AD, BE and CF. (2013D)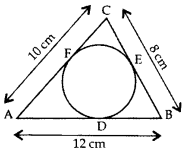

Solution:
Let AD = AF = x
BD = BE = y …[Two tangents drawn from and an external point are equal
CE = CF = z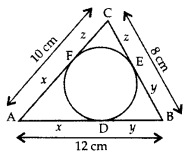

AB = 12 cm …[Given
∴ x + y = 12 cm …(i)
Similarly,
y + z = 8 cm …(ii)
and x + z = 10 cm …(iii)
By adding (i), (ii) & (iii)
2(x + y + z) = 30
x + y + z = 15 …[∵ x + y = 12
z = 15 – 12 = 3
Putting the value of z in (ii) & (iii),
y + 3 = 8
y = 8 – 3 = 5
x + 3 = 10
x = 10 – 3 = 7
∴ AD = 7 cm, BE = 5 cm, CF = 3 cm

Question 28.
The incircle of an isosceles triangle ABC, in which AB = AC, touches the sides BC, CA and AB at D, E and F respectively. Prove that BD = DC. (2014OD)
Solution:
Given: The incircle of ∆ABC touches the sides BC, CA and AB at D, E and F respectively.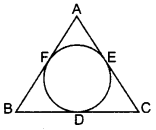

AB = AC
To prove: BD = CD
Proof: AF = AE ..(i)
BF = BD …(ii)
CD = CE …(iii)
Adding (i), (ii) and (iii), we get
AF + BF + CD = AE + BD + CE
⇒ AB + CD = AC + BD
But AB = AC …[Given
∴ CD = BD

Question 29.
In the figure, a ∆ABC is drawn to circumscribe a circle of radius 3 cm, such that the segments BD and DC are respectively 6 cm 9 cm of lengths 6 cm and 9 cm. If the area of ∆ABC is 54 cm2, then find the lengths of sides AB and AC. (2011D, 2011OD, 2015 OD)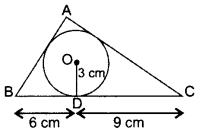

Solution:
Given: OD = 3 cm; OE = 3 cm; OF = 3 cm ar(∆ABC) = 54 cm2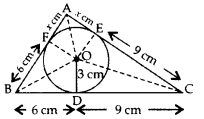

Joint: OA, OF, OE, OB and OC
Let AF = AE = x
BD = BF = 6 cm
CD = CE = 9 cm
∴ AB = AF + BF = x + 6 …(i)
AC = AE + CE = x + 9 …(ii)
BC = DB + CD = 6 + 9 = 15 cm …(iii)
In ∆ABC,
Area of ∆ABC = 54 cm2 …[Given
ar(∆ABC) = ar(∆BOC) + ar(∆AOC) + ar(∆AOB)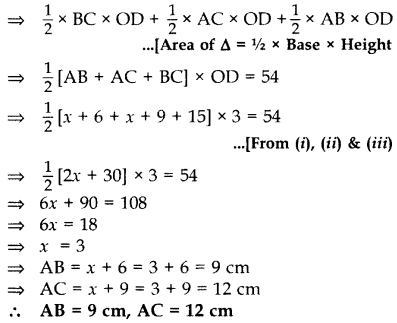

Question 30.
In the figure, a circle is inscribed in a ∆ABC, such that it touches the sides AB, BC and CA at points D, E and F respectively. If the lengths of sides AB, BC, and CA are 12 cm, 8 cm and 10 cm respectively, find the lengths of AD, BE and CF. (2016D)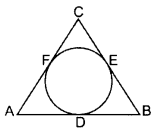

Solution:
AB = 12 cm, BC = 8 cm, CA = 10 cm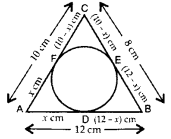

As we know,
AF = AD
CF = CE
BD = BE
Let AD = AF = x cm
then, DB = AB – AD
= (12 – x) cm
∴ BE = (12 – x) cm ..[Tangents drawn from an external point are equal
Similarly,
CF = CE = AC – AF = (10 – x) cm
BC = 8 cm …[Given
⇒ BE + CE = 8 ⇒ 12 – x + 10 – x = 8
⇒ 22 – 8 = 2x ⇒ 2x = 14
∴ x = 7 ∴ AD = x = 7 cm
BE = 12 – x = 12 – 7 = 5 cm
CF = 10 – x = 10 – 7 = 3 cm

Question 31.
In Figure, common tangents AB and CD to the two circles with lo, centres O1 and O2 intersect at E. Prove that AB = CD. (2014OD)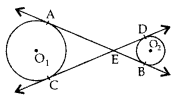

Solution:
EA = EC …(i) ….[Tangents drawn from an external point are equal
EB = ED …(ii)
EA + EB = EC + ED …[Adding (i) & (ii)
∴ AB = CD (Hence proved)

Question 32.
If from an external point P of a circle with centre O, two tangents PQ and PR are drawn such that ∠QPR = 120°, prove that 2PQ = PO. (2014D)
Solution:
∠OPQ = 12(∠QPR) ..[Tangents drawn from an external point are equal
= 12(120°) = 60° …[Tangent is ⊥ to the radius through the point of contact
∠OQP = 90°
In rt. ∆OQP, cos 60° = PQPO
12=PQPO ∴ 2PQ = PO

Question 33.
From a point T outside a circle of centre O, tangents TP and TQ are drawn to the circle. Prove that OT is the right bisector of line segment PQuestion (2015D)
Solution:
In ∆s’ TPC and TQC ….[Tangents drawn from an external point are equal
TP = TQ
TC = TC …[Common
∠1 = ∠2 …[TP and TQ are equally inclined to OT
∴ ∆TPC = ∆TQC … [SAS
∴ PC = QC …[CPCT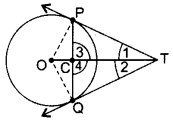

∠3 = ∠4 …(i)
⇒ ∠3 + 24 = 180° … [Linear pair
⇒ ∠3 + ∠3 = 180°…[From (i)
⇒ 2∠3 = 180° ⇒ ∠3 = 90°
∴ ∠3 = ∠4 = 90°
∴ OT is the right bisector of PQuestion

Question 34.
In the figure, two tangents RQ and RP are drawn from an external point R to the circle with centre O. If ∠PRQ = 120°, then prove that OR = PR + R. (2015OD)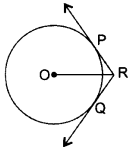

Solution:
Join OP and OO
∠OPR = 90°
PR = RQ … [Tangents drawn from an external point are equal
∠PRO = 12 ∠PRQ = 12 × 120° = 60°
Now, In ∆OPR,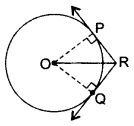

⇒ ∠OPR + ∠POR + ∠ORP = 180° …[∆ Rule
⇒ 90° + ∠POR + 60° = 180°
⇒ ∠POR + 150° = 180°
⇒ ∠POR = 30°
⇒ sin 30° = PROR ⇒ 12=PROR
⇒ OR = 2PR
⇒ OR = PR + QR (∵ PR = RQ) …(Hence proved)

Question 35.
In the figure, AP and BP are tangents to a circle with centre 0, such that AP = 5 cm and ∠APB = 60°. Find the length of chord AB. (2016D)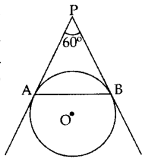

Solution:
PA = PB …[Tangents drawn from an external point are equal
Given:
∠APB = 60°
∠PAB = ∠PBA … (i) …(Angles opposite to equal sides
In ∆PAB, ∠PAB + ∠PBA + ∠APB = 180° …[Angle-sum-property of a ∆
⇒ ∠PAB + ∠PAB + 60° = 180°
⇒ 2∠PAB = 180° – 60o = 120°
⇒ ∠PAB = 60°
⇒ ∠PAB = ∠PBA = ∠APB = 60°
∴ APAB is an equilateral triangle
Hence, AB = AP = 5 cm …[∵ All sides of an equilateral A are equal

Question 36.
In the figure, from an external point P, two tangents PT and PS are drawn to a circle with centre O and radius r. If OP = 2r, show that ∠OTS = ∠OST = 30°. (2016OD)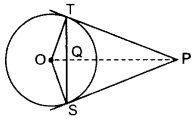

Solution:
Let ∠TOP = θ …[Tangent is ⊥ to the radius through the point of contact
∠OTP = 90°
OT = OS = r … [Given
In rt. ∆OTP, cos θ = OTOP
⇒ cos θ = r2r ⇒ cos θ = 12
⇒ cos θ = cos 60° ⇒ θ = 60°
∴ ∠TOS = 60° + 60° = 120°
In ATOS,
∠OTS = ∠OST …[Angles opposite to equal sides
In ∠TOS,
∠TOS + ∠OTS + ∠OST = 180° … [Angle-sum-property of a ∆
120° + ∠OTS + ∠OTS = 180° … [From (i)
2∠OTS = 180° – 120°
∠OTS = 60°/2 = 30°
∴ ∠OTS = ∠OST = 30°

Question 37.
In the given figure, PA and PB are tangents to the circle from an external point P. CD is another tangent touching the circle at Question If PA = 12 cm, QC = QD = 3 cm, then find PC + PD. (2017D)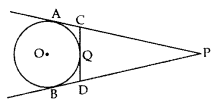

Solution: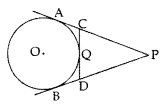

PA = PB = 12 cm …(i)
QC = AC = 3 cm …(ii)
QD = BD = 3 cm …(iii)
To find: PC + PD
= (PA – AC) + (PB – BD)
= (12 – 3) + (12 – 3) … [From (i), (ii) & (iii)
= 9 + 9 = 18 cm

Question 38.
In the figure, two circles touch each other at the point C. Prove that the common tangent to the circles at C, bisects the common tangent at P and Q. (2013 OD)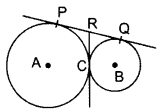

Solution:
To prove: PR = RQ
Proof: PR = RC … (i)
QR = RC
From (i) and (ii), PR = QR (Hence proved)

Circles Class 10 Important Questions Short Answer-II (3 Marks)

Question 39.
In the figure, a circle is inscribed in a triangle PQR with PQ = 10 cm, QR = 8 cm and PR = 12 cm. Find the lengths of QM, RN and PI. (2012OD)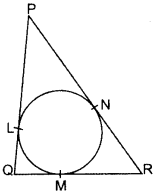

Solution:
Let PL = PN = x cm
QL = QM = y cm
RN = MR = z cm
PQ = 10 cm = x + y = 10 …(i)
QR = 8 cm = y + z = 8 …(ii)
PR = 12 cm = x + z = 12 …(iii)
By adding (i), (ii) and (iii),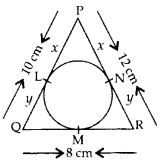

We get,
⇒ 2x + 2y + 2z = 10 + 8 + 12
⇒ 2(x + y + z) = 30
⇒ x + y + z = 15
⇒ 10 + z = 15 … [From (i)
∴ z = 15 – 10 = 5 cm
From (ii)
y + 5 = 8
y = 8 – 5
y = 3 cm
From (iii)
x + 5 = 12
x = 12 – 5
x = 7 cm
∴ QM = 3 cm, RN = 5 cm, PL = 7 cm

Question 40.
Prove that opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the centre of the circle. (2012D)
Solution:
1st method:
To prove. (i) ∠AOD + ∠BOC = 180°
(ii) ∠AOB + ∠COD = 180°
Proof. In ∆BPO and ∆BQO …[Tangents drawn from an external point are equal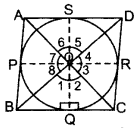

PO = 20 … [radii
BO = BO … [Common
∆BPO = ∆BQO … [SSS Congruency rule
∠8 = ∠1 …(i) (c.p.c.t.)
Similarly,
∠2 = ∠3, ∠4 = ∠5 and ∠6 = ∠7
∠1 + ∠2 + 23+ 24 + 25 + 26+ 27 + ∠8 = 360° …(Complete angles
∠1 + ∠2 + 22+ 25 + 25 + 26+ ∠6+ ∠1 = 360°
2(∠1 + ∠2 + 25 + 26) = 360°
∠BOC + ∠AOD = 180°…(i) [Proved part I
∠AOB + ∠BOC + ∠COD + ∠DOA = 360° …(Complete angles
∠AOB + ∠COD + 180o = 360° … [From (i)
∴ ∠AOB + ∠COD = 360° – 180o = 180° …(proved)

2nd method:
To prove:
(i) ∠6 + ∠8 = 180°
(ii) ∠5 + ∠7 = 180°
Proof. As AS and AP are tangents to the circle from a point A
∴ O lies on the bisector of ∠SAP
∴ ∠1 = 12 ∠BAD …(i)
Similarly BO, CO and DO are the bisectors of
∠ABC, ∠BCD and ∠ADC respectively. …(ii)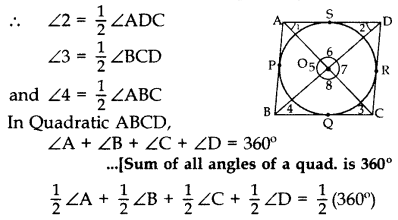

∴ ∠1 + ∠4 + ∠3 + ∠2 =180°…(iii) ..[From (1) & (ii)
In ∆AOD, ∠1 + ∠2 + 26 = 180° …[Angle-sum-Prop. of a ∆
In ∆BOC, ∠3 + ∠4 + ∠8 = 180° …(v)
Adding (iv) and (v)
(∠1 + ∠2 + 23 + 24) + 26 + 28 = 180° + 180°
180° + 26 + 28 = 180° + 180° … [From (iii)
∴∠6 + 28 = 180°
Now ∠5 + ∠6 + ∠7 + ∠8 = 360° … (Complete angles
(∠5 + ∠7) + (∠6 + ∠8) = 360°
(∠5 + ∠7) + 180° = 360°
∠5 + ∠7 = 360° – 180° = 180°
∠5 + ∠7 = 180°

Question 41.
Two tangents TP and TQ are drawn to a circle with centre O from an external point T. Prove that ∠PTQ = 2∠OPQ. (2017D)
Solution:
We are given a circle with centre O, an external point T and two tangents TP and TQ to the circle, where P, Q are the points of contact (see Figure).

We need to prove that:
∠PTQ = 2∠OPQ
Let ∠PTQ = θ
Now, TP = TQuestion ….[∵ Lengths of tangents drawn from an external pt. to a circle are equal
So, TPQ is an isosceles triangle.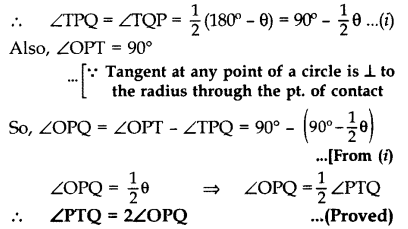

Circles Class 10 Important Questions Long Answer (4 Marks)

Question 42.
Prove that the tangent at any point of a circle is perpendicular to the radius through the point of contact. (2011OD, 2012OD, 2013D, 2014OD, 2015D)
Solution: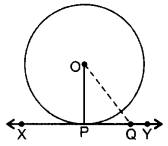

Given: XY is a tangent at point P to the circle with centre O.
To prove: OP ⊥ XY
Const.: Take a point Q on XY other than P and join to OQuestion
Proof: If point Q lies inside the circle, then XY will become a secant and not a tangent to the circle.
∴ OQ > OP
This happens with every point on the line XY except the point P.
OP is the shortest of all the distances of the point O to the points of XY
∴ OP ⊥ XY … [Shortest side is ⊥

Question 43.
Prove that the lengths of tangents drawn from an external point to a circle are equal. (2011D, 2012OD, 2013OD, 2014, 2015D & OD
2016D & OD, 2017D)
Solution:
Given: PT and PS are tangents from an external point P to the circle with centre O.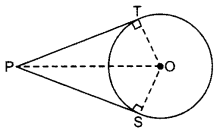

To prove: PT = PS
Const.: Join O to P,
T & S
Proof: In ∆OTP and
∆OSP,
OT = OS …[radii of same circle
OP = OP …[circle
∠OTP – ∠OSP …[Each 90°
∴ AOTP = AOSP …[R.H.S
PT = PS …[c.p.c.t

Question 44.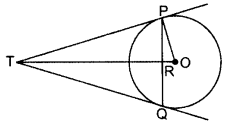

In the above figure, PQ is a chord of length 16 cm, of a circle of radius 10 cm. The tangents at P and Q intersect at a point T. Find the length of TP. (2014OD)
Solution:
TP = TQuestion .. [Tangents drawn from an external point
∆TPQ is an isosceles ∆ and TO is the bisector of ∠PTQ ,
OT ⊥ PQ …[Tangent is ⊥ to the radius through the point of contact
∴ OT bisects PQ
∴ PR = RQ = 16 = 8 cm …[Given
In rt. ∆PRO,
PR2 + RO2 = PO2 … [Pythagoras’ theorem
82 + RO2 = (10)2
RO2 = 100 – 64 = 36
∴ RO = 6 cm
Let TP = x cm and TR = y cm
Then OT = (y + 6) cm
In rt. ∆PRT, x2 = y2 + 82 …(i) …[Pythagoras’ theorem
In rt. ∆OPT,
OT2 = TP2 + PO2 …(Pythagoras’ theorem
(y + 6)2 = x2 + 102
y2 + 12y + 36 = y2 +64 + 100 …[From (i)
12y = 164 – 36 = 128 ⇒ y = 12812=323
Putting the value of y in (i),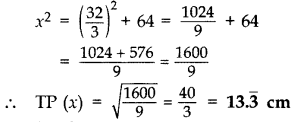

Question 45.
In the figure, tangents PQ and PR are drawn from an external point P to a circle with centre O, such that ∠RPQ = 30°. A chord RS is drawn parallel to the tangent PQuestion Find ∠RQS. (2015D)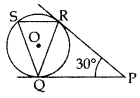

Solution:
PR = PO …[∵ Tangents drawn from an external point are equal
⇒ ∠PRQ = ∠PQR …[∵ Angles opposite equal sides are equal
In ∆PQR,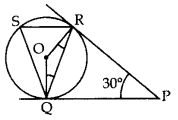

⇒ ∠PRQ + ∠RPQ + ∠POR = 180°…[∆ Rule
⇒ 30° + 2∠PQR = 180°
⇒ ∠PQR=(180−30)∘2
= 75°
⇒ SR || QP and QR is a transversal
∵ ∠SRQ = ∠PQR … [Alternate interior angle
∴ ∠SRO = 75° …..[Tangent is I to the radius through the point of contact
⇒ ∠ORP = 90°
∴ ∠ORP = ∠ORQ + ∠QRP
90° = ∠ORQ + 75°
∠ORQ = 90° – 75o = 150
Similarly, ∠RQO = 15°
In ∆QOR,
∠QOR + ∠QRO + ∠OQR = 180° …[∆ Rule
∴∠QOR + 15° + 15° = 180°
∠QOR = 180° – 30° = 150°
⇒ ∠QSR = 12∠QOR
⇒ ∠QSR = 150∘2 = 750 … [Used ∠SRQ = 75° as solved above
In ARSQ, ∠RSQ + ∠QRS + ∠RQS = 180° … [∆ Rule
∴ 75° + 75° + ∠RQS = 180°
∠RQS = 180° – 150o = 30°

Question 46.
Prove that the tangent drawn at the mid-point of an arc of a circle is parallel to the chord joining the end points of the arc. (2015OD)
Solution: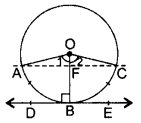

B is the mid point of arc (ABC)
OA = OC …[Radius
OF = OF …[Common
∴ ∠1 = ∠2 …[Equal angles opposite equal sides
∴ ∆OAF = ∆OCF (SAS)
∴ ∠AFO = ∠CFO = 90° …[c.p.c.t
⇒ ∠AFO = ∠DBO = 90° …[Tangent is ⊥to the radius through the point of contact
But these are corresponding angles,
∴ AC || DE

Question 47.
In the figure, O is the centre of a circle of radius 5 cm. T is a point such that OT = 13 cm and OT intersects circle at E. If AB is a tangent to the circle at E, find the length of AB, where TP and TQ are two tangents to the circle. (2016D)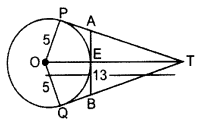

Solution:
∠OPT = 90° …[Tangent is ⊥ to the radius through the point of contact
We have, OP = 5 cm, OT = 13 cm
In rt. ∆OPT,
OP2 + PT2 = OT? …[Pythagoras’ theorem
⇒ (5)2 + PT2 = (13)2
⇒ PT2 = 169 – 25 = 144 cm
⇒ PT = 144−−−√
= 12 cm
OP = OQ = OE = 5 cm … [Radius of the circle
ET = OT – OE
= 13 – 5 = 8 cm
Let, PA = x cm, then AT = (12 – x) cm
PA = AE = x cm …[Tangent drawn from an external point
In rt. ∆AET,
AE2 + ET2 = AT2 …(Pythagoras’ theorem
⇒ x2 + (8)2 = (12 – x)2
⇒ x2 + 64 = 144 + x2 – 24x
⇒ 24x = 144 – 64
x = 8024=103 cm
AB = AE + EB = AE + AE = 2AE = 2x :
∴ AB = 2(103)=203cm=623 cm
or 6.67 cm or 6.6 cm

Question 48.
In the figure, two equal circles, with centres 0 and O’, touch each other A at X. OO’ produced meets the circle with centre O’ at A. AC is tangent to the circle with centre O, at the point C. O’D is perpendicular to AC. Find the value of 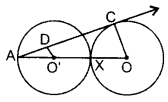DO′CO. (2016OD)

Solution:
Given: Two equal circles, with centres O and O’, touch each other at point X. OO’ is produced to meet the circle with centre (at A. AC is tangent to the circle with centre O, at the point C. OʻD is perpendicular to AC.
To find: = DO′CO
Proof: ∠ACO = 90° … [Tangent is ⊥ to the radius through the point of contact
In ∆AO’D and ∆AOC
∠O’AD = ∠OAC …(Common
∴ ∠ADO = ∠ACO …[Each 90°
∴ ∆AO’D ~ ∴AOC …(AA similarity
AO′AO=DO′CO … [In ~ As corresponding sides are proportional
r3r=DO′CO …[Let AO’ = O’X = OX = r ⇒ AO = r +r+ r = 3r
∴ DO′CO=13

Question 49.
In the figure, l and m are two parallel tangents to a circle with centre O, touching the circle at A and B respectively. Another tangent at C intersects the line I at D and m at E. Prove that ∠DOE = 90°. (2013D)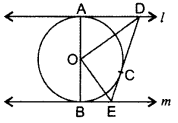

Solution:
Proof: Let I be XY and m be XY’
∠XDE + ∠X’ED = 180° … [Consecutive interior angles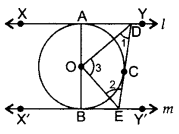

12XDE + 12∠X’ED =
= 12 (180°)
= ∠1 + ∠2 = 90° …[OD is equally inclined to the tangents
In ∆DOE, ∠1 + ∠2 + 23 = 180° …[Angle-sum-property of a ∆
90° + 23 = 180°
⇒ ∠3 = 180° – 90o = 90°
∴ ∠DOE = 90° …(proved)

Question 50.
In the figure, the sides AB, BC and CA of triangle ABC touch a circle with centre o and radius r at P, Q and R. respectively. (2013OD)
Prove that:
(i) AB + CQ = AC + BQ
(ii) Area (AABC) = 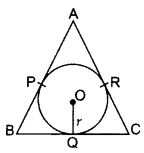12 (Perimeter of ∆ABC ) × r

Solution: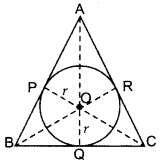

Part I:
Proof: AP = AR …(i)
BP = BQ … (ii)
CQ = CR … (iii)
Adding (i), (ii) & (iii)
AP + BP + CQ
= AR + BQ + CR
AB + CQ = AC + BQ
Part II: Join OP, OR, OQ, OA, OB and OC
Proof: OQ ⊥ BC; OR ⊥ AC; OP ⊥ AB
ar(∆ABC) = ar(∆AOB) + ar(∆BOC) + ar (∆AOC)
Area of (∆ABC)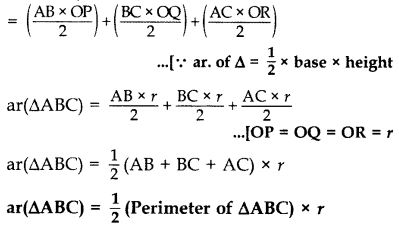

Question 51.
In the figure, a triangle ABC is drawn to circumscribe a circle of radius 4 cm, such that the segments BD and DC are of lengths 8 cm and 6 cm respectively. Find the sides AB and AC. (2014OD)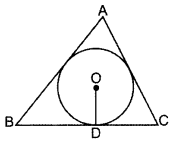

Solution: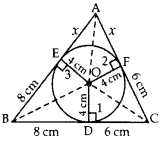

Let AE = x ∴ AF = x
BC = 8 + 6 = 14 cm
AB = (x + 8) cm
AC = (x + 6) cm
∠1 = ∠2 = 23 = 90° …[ Tangent is ⊥ to the radius B [through the point of contact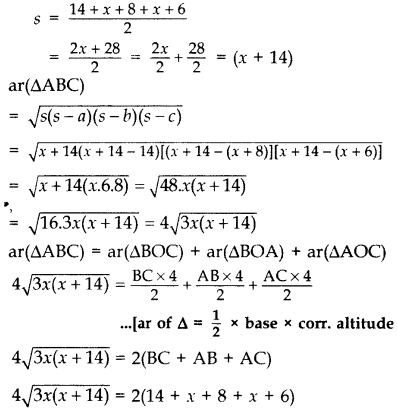

43x(x+14)−−−−−−−−−√ = 2(2x + 28)
43x(x+14)−−−−−−−−−√ = 2.2(x + 14)
3x(x + 14) = (x + 14)2 … [Squaring both sides
3x(x + 14) – (x + 14)2 = 0
(x + 14) [3x – (x + 14)] = 0
(x + 14) (2x – 14) = 0
x = -14 or x = 7
∴ x = 7 … [As side of ∆ cannot be -ve
∴ AB = x + 8 = 15 cm
and AC = x + 6 = 13 cm

Question 52.
Prove that the line segment joining the points of contact of two parallel tangents of a circle, passes through its centre. (2014 D)
Solution: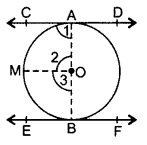

Given: CD and EF are two C parallel tangents at points A and B of a circle with centre O.
To prove: AB passes through centre O or AOB is diameter of the circle.
Const.: Join OA and OB. Draw OM || CD.
Proof: ∠1 = 90° … (i)
…[∵ Tangent is I to the radius through the point of contact
OM || CD
∴ ∠1 + ∠2 = 180° …(Co-interior angles
90° + ∠2 = 180° …[From (i)
∠2 = 180° – 90o = 90°
Similarly, ∠3 = 90°
∠2 + ∠3 = 90° + 90° = 180°
∴ AOB is a straight line.
Hence AOB is a diameter of the circle with centre O.
∴ AB passes through centre 0.

Class 10 Maths Notes Chapter 10 Circles

Circle: A circle is a collection of all points in a plane which are at a constant distance from a fixed point.

Centre: The fixed point is called the centre.

Radius: The constant distance from the centre is called the radius.

Chord: A line segment joining any two points on a circle is called a chord.

Diameter: A chord passing through the centre of the circle is called diameter. It is the longest chord.

Tangent: When a line meets the circle at one point or two coincidings The line is known as points, a tangent.
The tangent to a circle is perpendicular to the radius through the point of contact.
⇒ OP ⊥ AB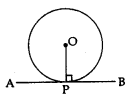

The lengths of the two tangents from an external point to a circle are equal.
⇒ AP = PB

Length of Tangent Segment
PB and PA are normally called the lengths of tangents from outside point P.

Properties of Tangent to Circle

Theorem 1: Prove that the tangent at any point of a circle is perpendicular to the radius through the point of contact.
Given: XY is a tangent at point P to the circle with centre O.
To prove: OP ⊥ XY
Construction: Take a point Q on XY other than P and join OQ
Proof: If point Q lies inside the circle, then XY will become a secant and not a tangent to the circle
OQ > OP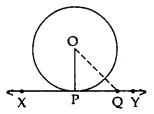

This happens with every point on line XY except point P. OP is the shortest of all the distances of point O the points of XY
OP ⊥ XY …[Shortest side is the perpendicular]

Theorem 2: A line drawn through the endpoint of a radius and perpendicular to it, is tangent to the circle.
Given: A circle C(O, r) and a line APB is perpendicular to OP, where OP is the radius.
To prove: AB is tangent at P.
Construction: Take a point Q on line AB, different from P, and join OQ.
Proof: Since OP ⊥ AB
OP < OQ ⇒ OQ > OP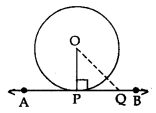

Point Q lies outside the circle.
Therefore, every point on AB, other than P, lies outside the circle.
This shows that AB meets the circle at point P.
Hence, AP is tangent to the circle at P.

Theorem 3: Prove that the lengths of tangents drawn from an external point to a circle are equal
Given: PT and PS are tangents from an external point P to the circle with centre O.
To prove: PT = PS
Construction: Join O to P, T and S.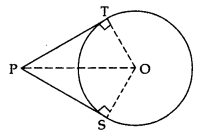

Proof: In ∆OTP and ∆OSP.
OT = OS …[radii of the same circle]
OP = OP …[common]
∠OTP = ∠OSP …[each 90°]
∆OTP = ∆OSP …[R.H.S.]
PT = PS …[c.p.c.t.]

Note: If two tangents are drawn to a circle from an external point, then:

• They subtend equal angles at the centre i.e., ∠1 = ∠2.
• They are equally inclined to the segment joining the centre to that point i.e., ∠3 = ∠4.
  ∠OAP = ∠OAQ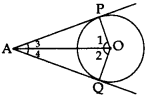
  

Here Is The Class 10 Maths All NCERT Solutions In Hindi + English With Extra Questions, Notes And Important Questions

• Chapter 1 Real Numbers
• Chapter 2 Polynomials
• Chapter 3 Pair of Linear Equations in Two Variables
• Chapter 4 Quadratic Equations
• Chapter 5 Arithmetic Progressions
• Chapter 6 Triangles
• Chapter 7 Coordinate Geometry
• Chapter 8 Introduction to Trigonometry
• Chapter 9 Applications of Trigonometry
• Chapter 10 Circle
• Chapter 11 Constructions
• Chapter 12 Areas related to Circles
• Chapter 13 Surface Areas and Volumes
• Chapter 14 Statistics
• Chapter 15 Probability