Class 10 Maths Chapter 6 Triangles (English + Hindi) NCERT Solutions

Class 10 Maths Chapter 6 Triangles (English + Hindi) NCERT Solutions

Table Of Content

• Ex.6.1
• Ex.6.2
• Ex.6.3
• Ex.6.4
• Ex.6.5
• Ex.6.6
• Extra Questions for Class 10 Maths Triangles
• Triangles Class 10 Notes Maths Chapter 6
• NCERT Exemplar Class 10 Maths Chapter 6 Triangles
• Important Questions for Class 10 Maths Chapter 6 Triangles
• Triangles Class 10 Notes

Ex 6.1 Class 10 Maths Question 1.
Fill in the blanks by using the correct word given in brackets.
(i) All circles are ……………. . (congruent/similar)
(ii) All squares are …………… . (similar/congruent)
(iii) All …………….. triangles are similar. (isosceles/equilateral)
(iv) Two polygons of the same number of sides are similar, if
(a) their corresponding angles are …………… and
(b) their corresponding sides are …………… (equal/proportional)
Solution:

Ex 6.1 Class 10 Maths Question 2.
Give two different examples of pairs of
(i) similar figures.
(ii) non-similar figures.
Solution:

Ex 6.1 Class 10 Maths Question 3.
State whether the following quadrilaterals are similar or not.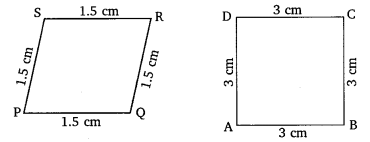

Solution: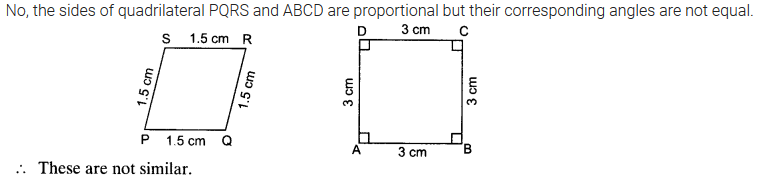

Triangles Class 10 Ex 6.2

Ex 6.2 Class 10 Maths Question 1.
In the given figure (i) and (ii), DE || BC. Find EC in (i) and AD in (ii).

Solution:

Ex 6.2 Class 10 Maths Question 2.
E and F are points on the sides PQ and PR respectively of a ∆PQR. For each of the following cases, state whether EF || QR:
(i) PE = 3.9 cm, EQ = 3 cm, PF = 3.6 cm and FR = 2.4 cm
(ii) PE = 4 cm, QE = 4.5 cm, PF = 8 cm and RF = 9 cm
(iii) PQ = 1.28 cm, PR = 2.56 cm, PE = 0.18 cm and PF = 0.36 cm
Solution:

Ex 6.2 Class 10 Maths Question 3.
In the given figure, if LM || CB and LN || CD.
Prove that 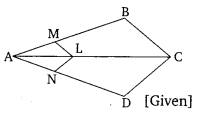AMAB=ANAD∙

Solution: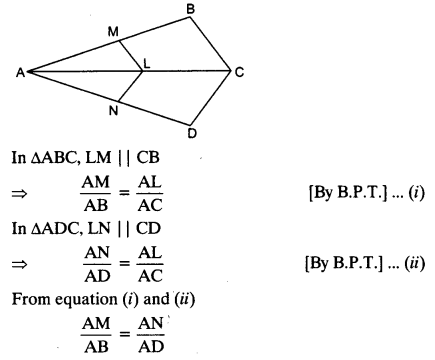

Ex 6.2 Class 10 Maths Question 4.
In the given figure, DE || AC and DF || AE.
Prove that BFFE=BEEC∙

Solution:

Ex 6.2 Class 10 Maths Question 5.
In the given figure, DE || OQ and DF || OR. Show that EF || QR.

Solution: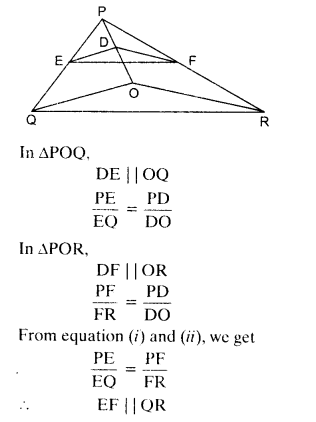

Ex 6.2 Class 10 Maths Question 6.
In the given figure, A, B and C are points on OP, OQ and OR respectively such that AB || PQ and AC || PR. Show that BC || QR.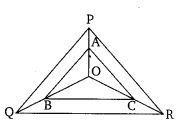

Solution:

Ex 6.2 Class 10 Maths Question 7.
Using B.P.T., prove that a line drawn through the mid-point of one side of a triangle parallel to another side bisects the third side. (Recall that your have proved it in class IX)
Solution:

Ex 6.2 Class 10 Maths Question 8.
Using converse of B.P.T., prove that the line joining the mid-points of any two sides of a triangle is parallel to the third side.  (Recall that your have done it in class IX)
Solution: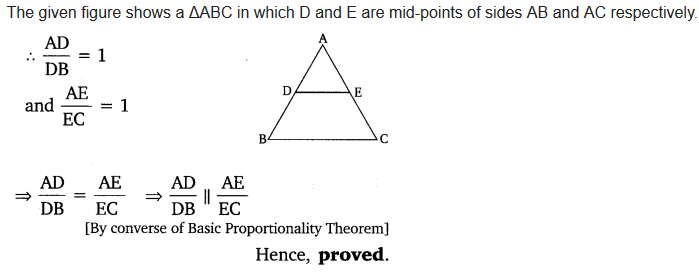

Ex 6.2 Class 10 Maths Question 9.
ABCD is a trapezium in which AB || DC and its diagonals intersect each other at the point O. Show that AOBO=CODO∙
Solution: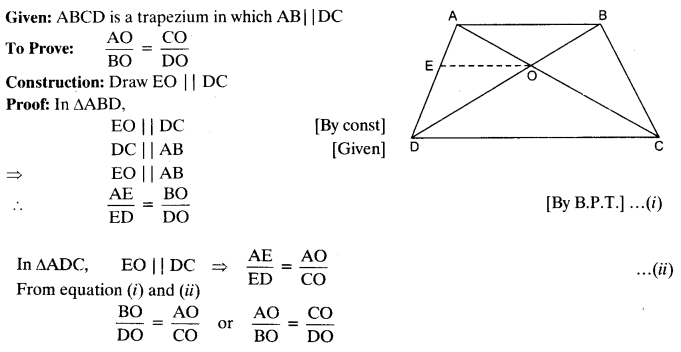

Ex 6.2 Class 10 Maths Question 10.
The diagonals of a quadrilateral ABCD intersect each other at the point O such that AOBO=CODO∙ Show that ABCD is a trapezium.
Solution:

Triangles Class 10 Ex 6.3

Ex 6.3 Class 10 Maths Question 1.
State which pairs of triangles in the given figures are similar. Write the similarity criterion used by you for answering the question and also write the pairs of similar triangles in the symbolic form :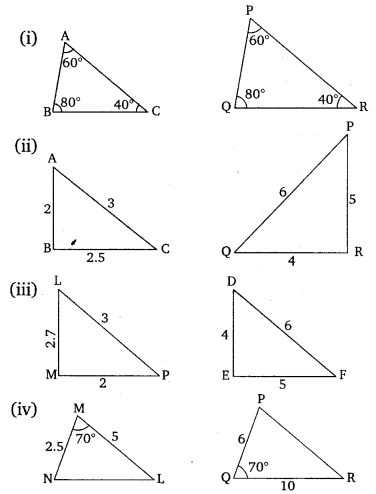

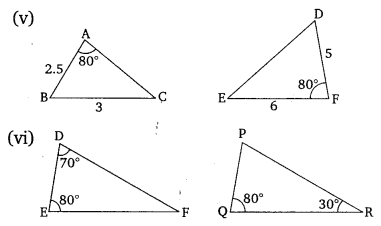
Solution: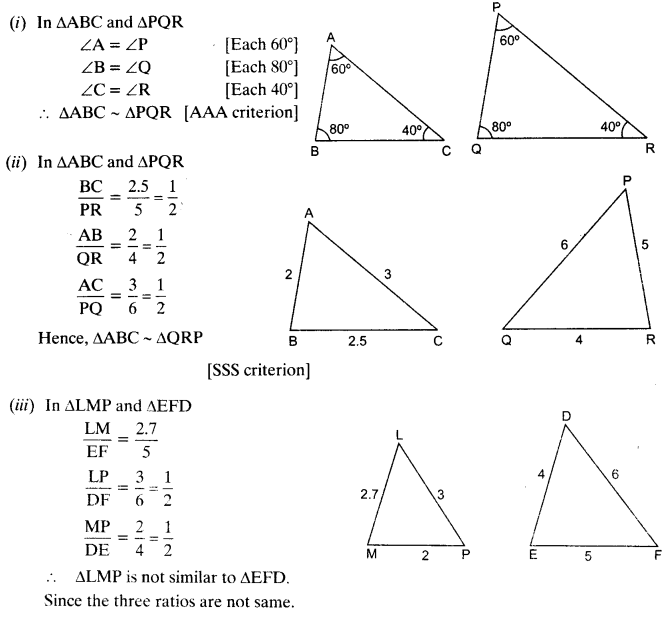

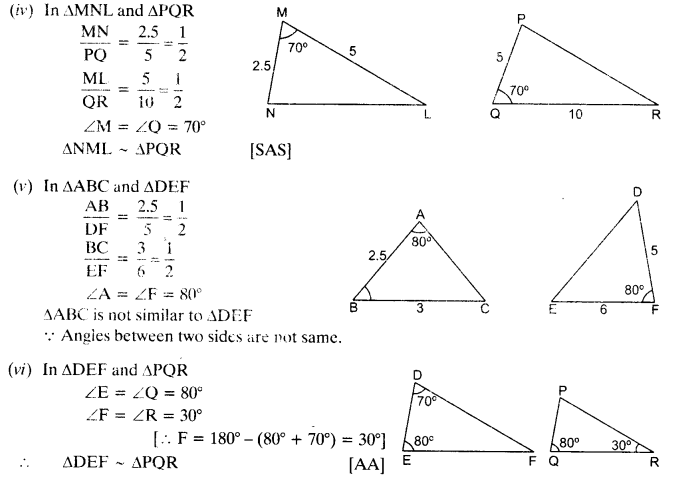
Ex 6.3 Class 10 Maths Question 2.
In the given figure, ∆ODC ~ ∆OBA, ∠BOC = 125° and ∠CDO = 70°. Find ∠DOC, ∠DCO and ∠OAB.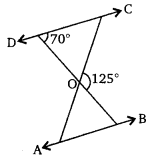

Solution: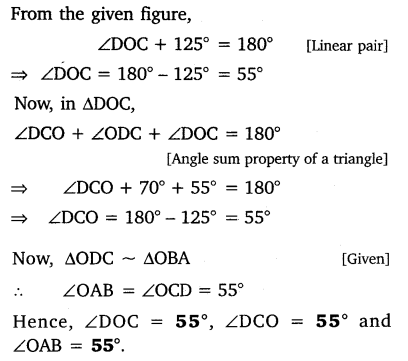

NCVT MIS

Ex 6.3 Class 10 Maths Question 3.
Diagonals AC and BD of a trape∠ium ABCD with AB || DC intersect each other at the point O. Using a similarity criterion for two triangles, show that OAOC=OBOD∙
Solution:

Ex 6.3 Class 10 Maths Question 4.
In the given figure, 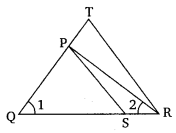QRQS=QTPR and ∠1 = ∠2. show that ∆PQR ~ ∆TQR.

Solution:

Ex 6.3 Class 10 Maths Question 5.
S and T are points on sides PR and QR of ∆PQR such that ∠P = ∠RTS. Show that ∆RPQ ~ ∆RTS.
Solution:

Ex 6.3 Class 10 Maths Question 6.
In the given figure, if ∆ABE ≅ ∆ACD, show that ∆ADE ~ ∆ABC.

Solution:

Ex 6.3 Class 10 Maths Question 7.
In the given figure, altitudes AD and CE of ∆ABC intersect each other at the point P. Show that:
(i) ∆AEP ~ ∆CDP
(ii) ∆ABD ~ ∆CBE
(iii) ∆AEP ~ ∆ADB
(iv) ∆PDC ~ ∆BEC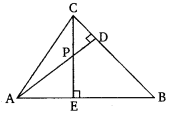

Solution: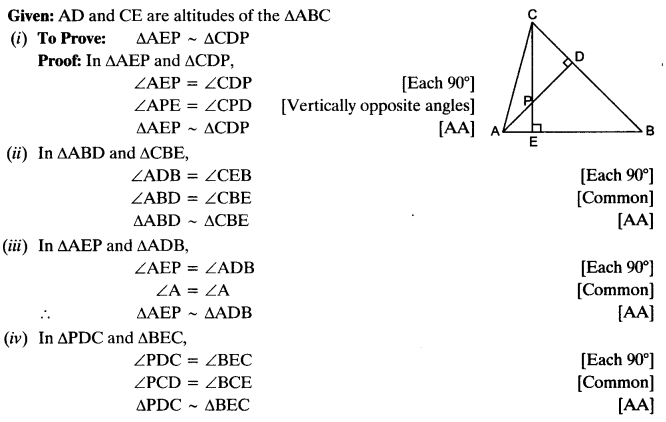

Ex 6.3 Class 10 Maths Question 8.
E is a point on the side AD produced of a parallelogram ABCD and BE intersects CD at F. Show that ∆ABE ~ ∆CFB.
Solution: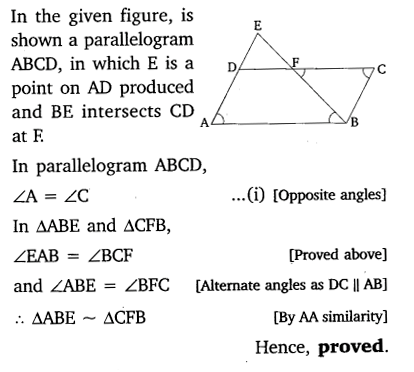

Ex 6.3 Class 10 Maths Question 9.
In the given figure, ABC and AMP are two right triangles, right angled at B and M respectively. Prove that: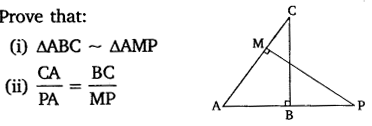

Solution: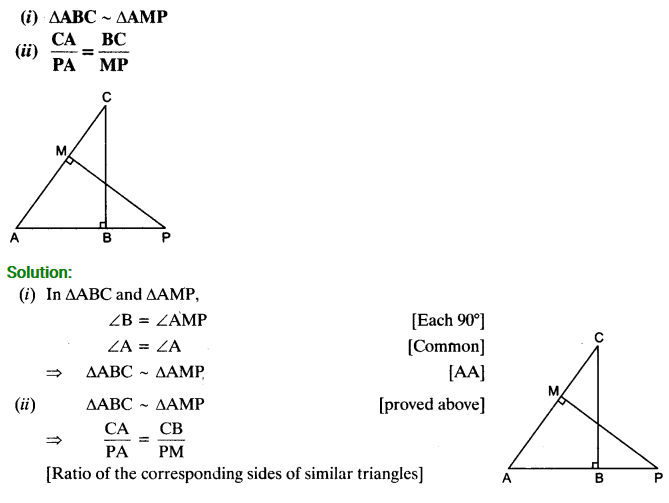

Ex 6.3 Class 10 Maths Question 10.
CD and GH are respectively the bisectors of ∠ACB and ∠EGF such that D and H lie on sides AB and FE of ∆ABC and ∆EFG respectively. If ∆ABC ~ ∆FEG, show that

Solution: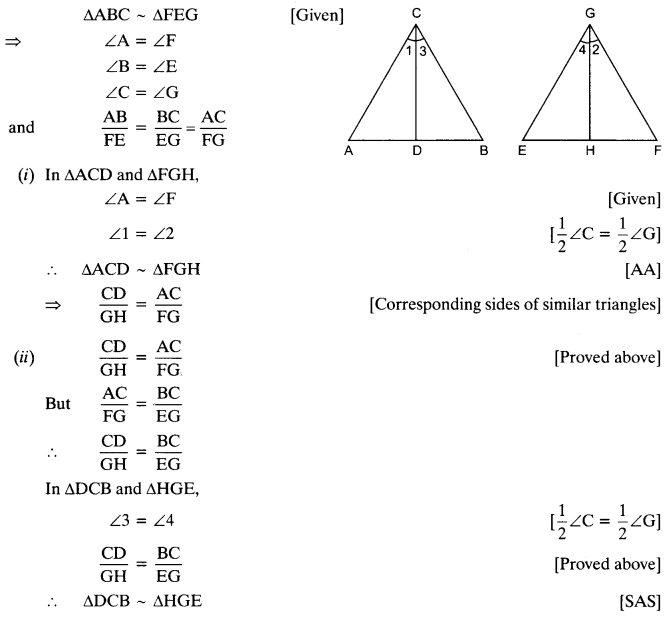

Ex 6.3 Class 10 Maths Question 11.
In the given figure, E is a point on side CB produced of an isosceles triangle ABC with AB = AC. If AD ⊥ BC and EF ⊥ AC, prove that ∆ABD ~ ∆ECF.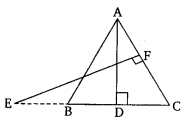

Solution:

Ex 6.3 Class 10 Maths Question 12.
Sides AB and BC and median AD of a triangle ABC are respectively proportional to sides PQ and QR and median PM of ∆PQR (see in given figure). Show that ∆ABC ~ ∆bPQR.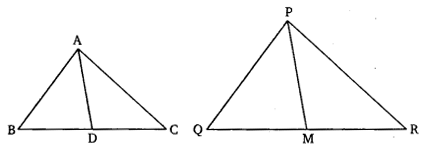

Solution: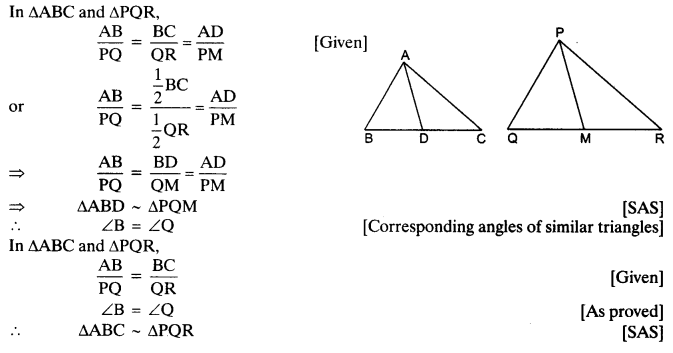

Ex 6.3 Class 10 Maths Question 13.
D is a point on the side BC of a triangle ABC, such that ∠ADC = ∠BAC. Show that CA² = CB.CD.
Solution: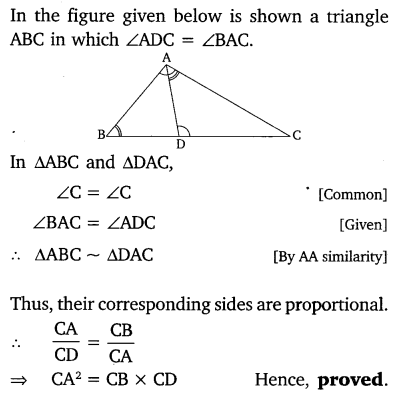

Ex 6.3 Class 10 Maths Question 14.
Sides AB and AC and median AD of a triangle ABC are respectively proportional to sides PQ and PR and median PM of another triangle PQR. Show that ∆ABC ~ ∆PQR.
Solution: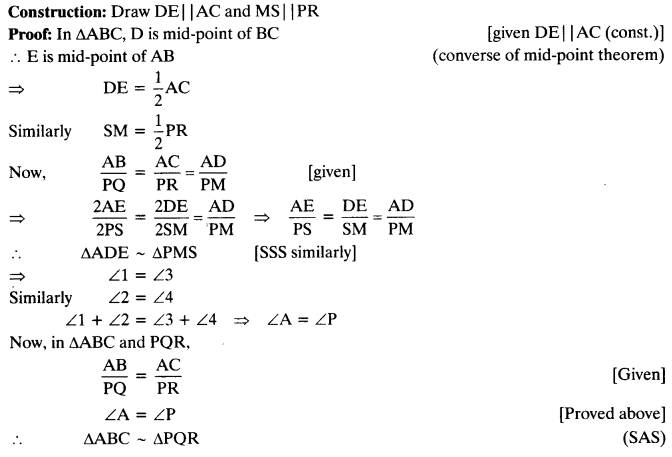

Ex 6.3 Class 10 Maths Question 15.
A vertical pole of length 6 m casts a shadow 4 m long on the ground and at the same time a tower casts a shadow 28 m long. Find the height of the tower.
Solution:

Ex 6.3 Class 10 Maths Question 16.
If AD and PM are medians of triangles ABC and PQR respectively, where
∆ABC ~ ∆PQR. Prove that ABPQ=ADPM∙
Solution: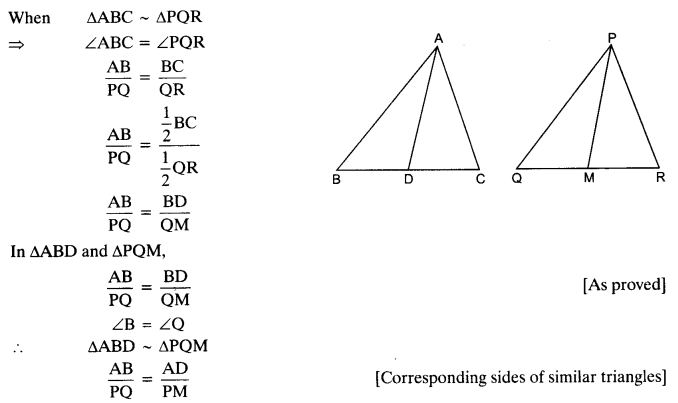

Triangles Class 10 Ex 6.4

Ex 6.4 Class 10 Maths Question 1.
Let ∆ABC ~ ∆DEF and their areas be, respectively, 64 cm2 and 121 cm2. If EF = 15.4 cm, find BC.
Solution: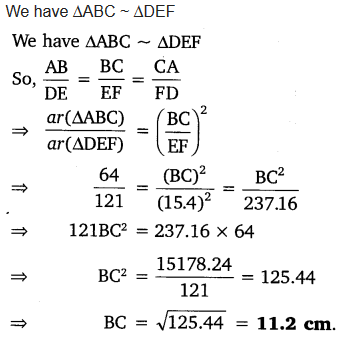

Ex 6.4 Class 10 Maths Question 2.
Diagonals of a trapezium ABCD with AB || DC intersect each other at the point O. If AB = 2 CD, find the ratio of the areas of triangles AOB and COD.
Solution: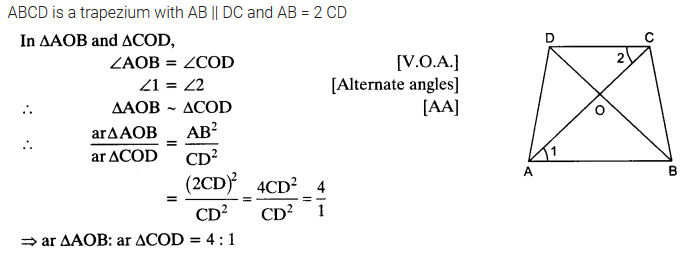

Ex 6.4 Class 10 Maths Question 3.
In the given figure, ABC and DBC are two triangles on the same base BC. If AD intersects BC at O, show that: 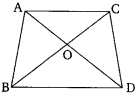ar(ABC)ar(DBC)=AODO

Solution: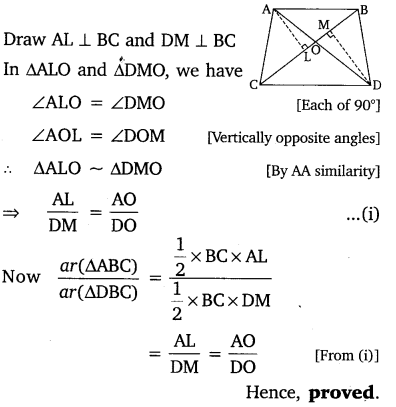

Ex 6.4 Class 10 Maths Question 4.
If the areas of two similar triangles are equal, prove that they are congruent.
Solution: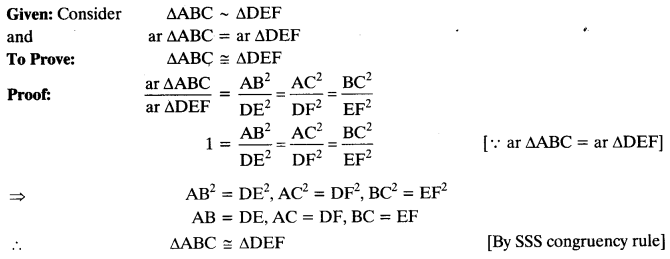

Ex 6.4 Class 10 Maths Question 5.
D, E and F are respectively the mid-points of sides AB, BC and CA of ∆ABC. Find the ratio of the areas of ∆DEF and ∆ABC.
Solution: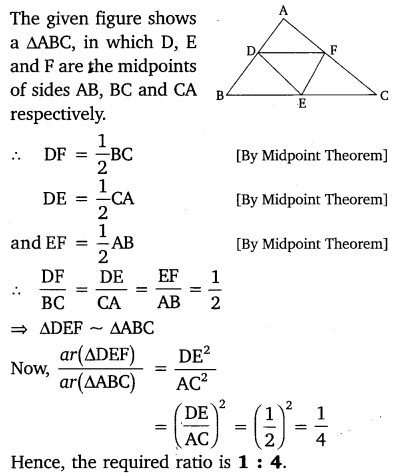

Ex 6.4 Class 10 Maths Question 6.
Prove that the ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding medians.
Solution:

Ex 6.4 Class 10 Maths Question 7.
Prove that the area of an equilateral triangle described on one side of a square is equal to half the area of the equilateral triangle described on one of its diagonals.
Solution: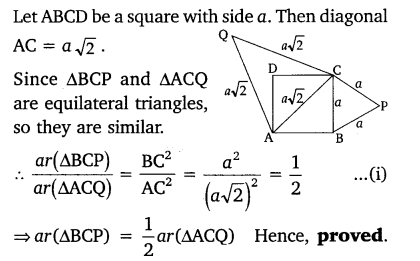

Ex 6.4 Class 10 Maths Question 8.
Tick the correct answer and justify
(i) ABC and BDE are two equilateral triangles such that D is the mid-point of BC. Ratio of the areas of triangles ABC and BDE is
(a) 2 :1
(b) 1:2
(c) 4 :1
(d) 1:4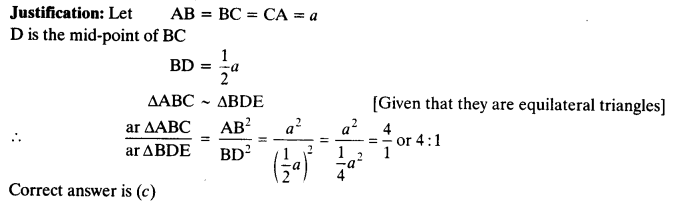

(ii) Sides of two similar triangles are in the ratio 4 : 9. Areas of these triangles are in the ratio
(a) 2 : 3
(b) 4 : 9
(c) 81 : 16
(d) 16 : 81

Triangles Class 10 Ex 6.5

Ex 6.5 Class 10 Maths Question 1.
Sides of triangles are given below. Determine which of them are right triangles. In case of a right triangle, write the length of its hypotenuse.
(i) 7 cm, 24 cm, 25 cm
(ii) 3 cm, 8 cm, 6 cm
(iii) 50 cm, 80 cm, 100 cm
(iv) 13 cm, 12 cm, 5 cm
Solution:

Ex 6.5 Class 10 Maths Question 2.
PQR is a triangle right angled at P and M is a point on QR such that PM ⊥ QR. Show that PM2 = QM X MR.
Solution: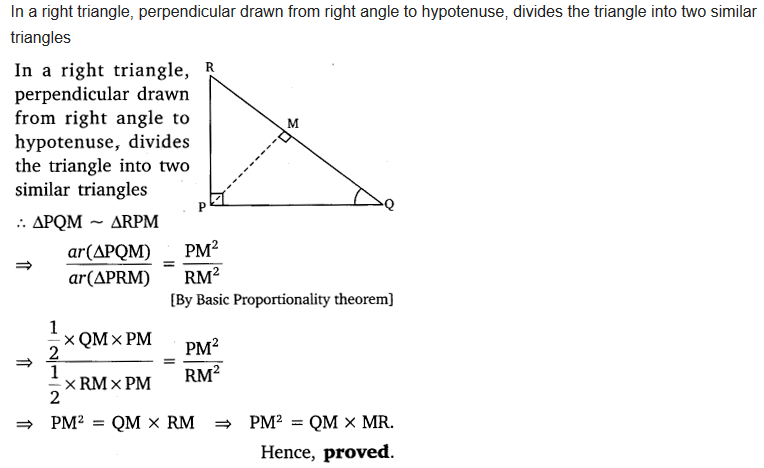

Ex 6.5 Class 10 Maths Question 3.
In the given figure, ABD is a triangle right angled at A and AC i. BD. Show that
(i) AB2 = BC.BD
(ii) AC2 = BC.DC
(iii) AD2 = BD.CD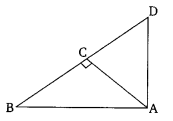

Solution:

Ex 6.5 Class 10 Maths Question 4.
ABC is an isosceles triangle right angled at C. Prove that AB2 = 2AC2.
Solution: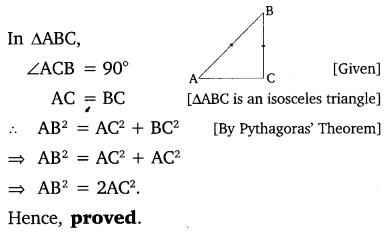

Ex 6.5 Class 10 Maths Question 5.
ABC is an isosceles triangle with AC = BC. If AB2 = 2AC2 , Prove that ABC is a right triangle.
Solution: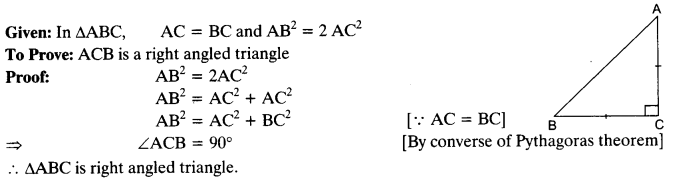

Ex 6.5 Class 10 Maths Question 6.
ABC is an equilateral triangle of side la. Find each of its altitudes.
Solution: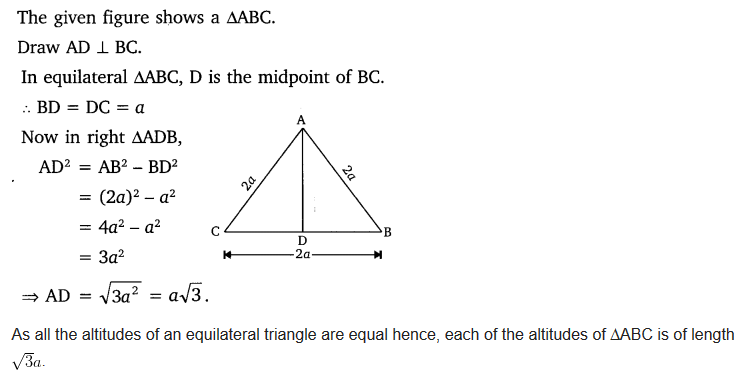

Ex 6.5 Class 10 Maths Question 7.
Prove that the sum of the squares of the sides of a rhombus is equal to the sum of the squares of its diagonals.
Solution:

Ex 6.5 Class 10 Maths Question 8.
In the given figure, O is a point in the interior of a triangle ABC, OD ⊥ BC, OE ⊥ AC and OF ⊥ AB. Show that
(i) OA2 + OB2 + OC2 – OD2 – OE2 – OF2 = AF2 + BD2 + CE2
(ii) AF2 + BD2 + CE2 = AE2 + CD2 + BF2.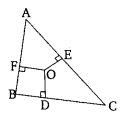

Solution: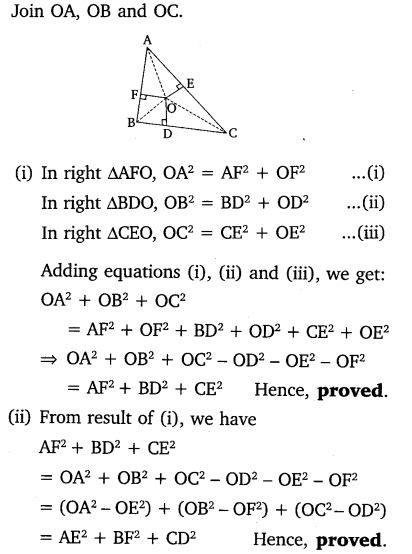

Ex 6.5 Class 10 Maths Question 9.
A ladder 10 m long reaches a window 8 m above the ground. ind the distance of the foot of the ladder from base of the wall.
Solution:

Ex 6.5 Class 10 Maths Question 10.
A guy wire attached to a vertical pole of height 18 m is 24 m long and has a stake attached to the other end. How far from the base of the pole should the stake be driven so that the wire will be taut?
Solution:

Ex 6.5 Class 10 Maths Question 11.
An aeroplane leaves an airport and flies due north at a speed of 1000 km per hour. At the same time, another aeroplane leaves the same airport and flies due west at a speed of 1200 km per hour. How far apart will be the two planes after 112 hours?
Solution: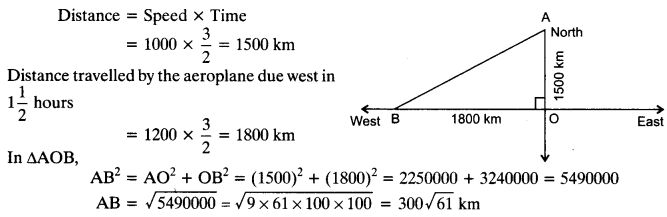

Ex 6.5 Class 10 Maths Question 12.
Two poles of heights 6 m and 11m stand on a plane ground. If the distance between the feet of the poles is 12 m, find the distance between their tops.
Solution:

Ex 6.5 Class 10 Maths Question 13.
D and E are points on the sides CA and CB respectively of a triangle ABC right angled at C. Prove that AE2 + BD2 = AB2 + DE2.
Solution: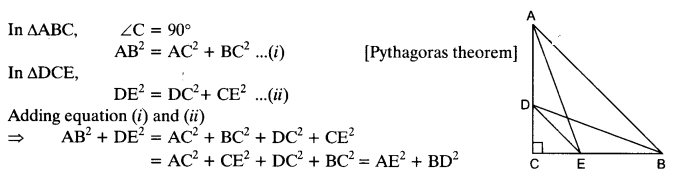

Ex 6.5 Class 10 Maths Question 14.
The perpendicular from A on side BC of a ∆ABC intersects BC at D such that DB = 3CD (see the figure). Prove that 2AB2 = 2AC2 + BC2.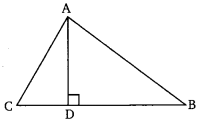

Solution:

Ex 6.5 Class 10 Maths Question 15.
In an equilateral triangle ABC, D is a point on side BC, such that BD = 13BC. Prove that 9AD2 = 7AB2.
Solution: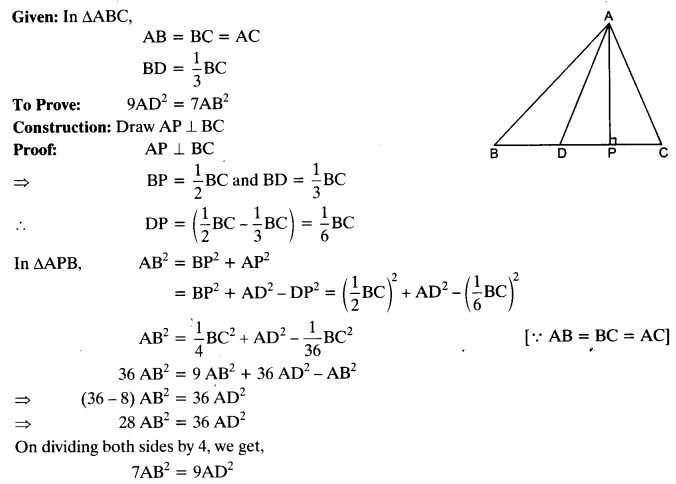

Ex 6.5 Class 10 Maths Question 16.
In an equilateral triangle, prove that three times the square of one side is equal to four times the square of one of its altitudes.
Solution: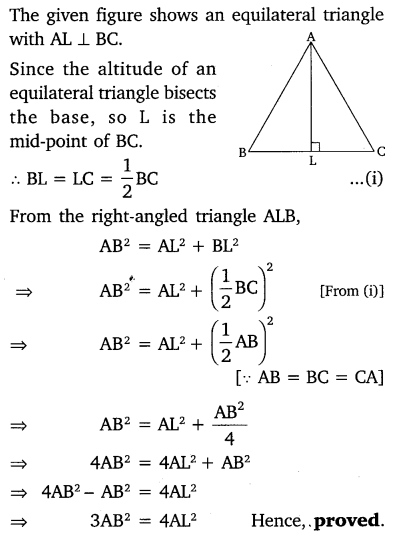

Ex 6.5 Class 10 Maths Question 17.
Tick the correct answer and justify : In ∆ABC, AB = 63–√cm, AC = 12 cm and BC = 6 cm. The angle B is:
(a) 120°
(b) 60°
(c) 90°
(d) 45
Solution: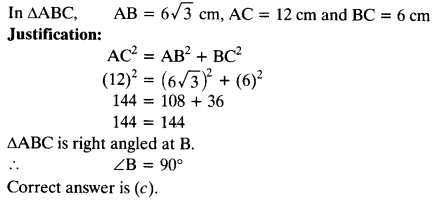

Triangles Class 10 Ex 6.6

Ex 6.6 Class 10 Maths Question 1.
In the given figure, PS is the bisector of ∠QPR of ∆PQR. Prove that 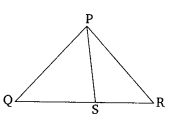QSSR=PQPR

Solution: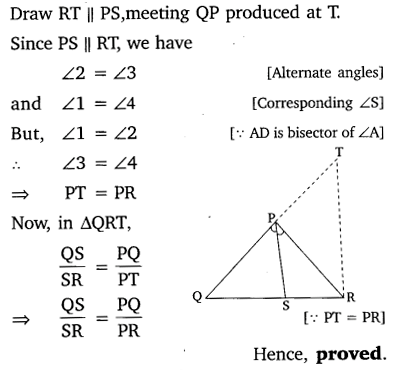

Ex 6.6 Class 10 Maths Question 2.
In the given figure, D is a point on hypotenuse AC of ∆ABC, DM ⊥ BC and DN ⊥ AB. Prove that:
(i) DM2 = DN X MC
(ii) DN2 = DM X AN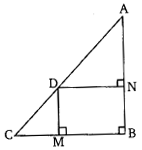

Solution:

Ex 6.6 Class 10 Maths Question 3.
In the given figure, ABc is triangle in which ∠ABC > 90° and AD ⊥ CB produced. Prove that AC2 = AB2 + BC2  + 2BC X BD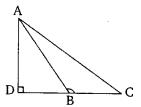

Solution:

Ex 6.6 Class 10 Maths Question 4.
In the given figure, ABC is atriangle in which ∠ABC 90° and AD ⊥ CB. Prove that AC2 = AB2 + BC2 – 2BC X BD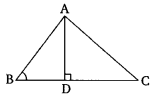

Solution:

Ex 6.6 Class 10 Maths Question 5.
In the given figure, Ad is a median of a triangle ABC and AM ⊥ BC. Prove that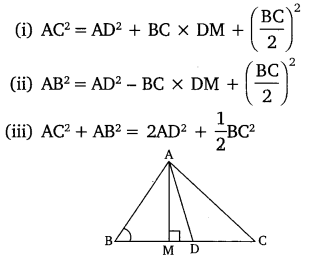

Solution:

Ex 6.6 Class 10 Maths Question 6.
Prove that the sum of the squares of the diagonals of parallelogram is equal to the sum of the squares of its sides.
Solution: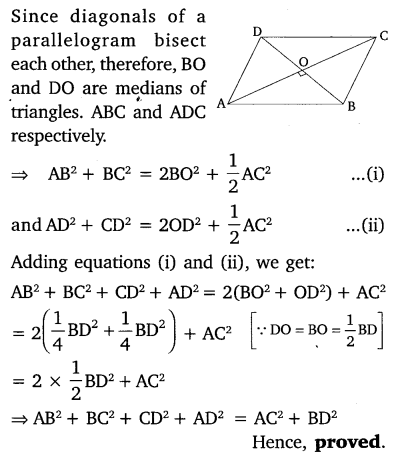

Ex 6.6 Class 10 Maths Question 7.
In the given figure, two chords AB and CD intersect each other at the point P. Prove that:
(i) ∆APC ~∆DPB
(ii) AP X PB = CP X DP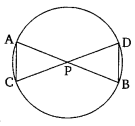

Solution: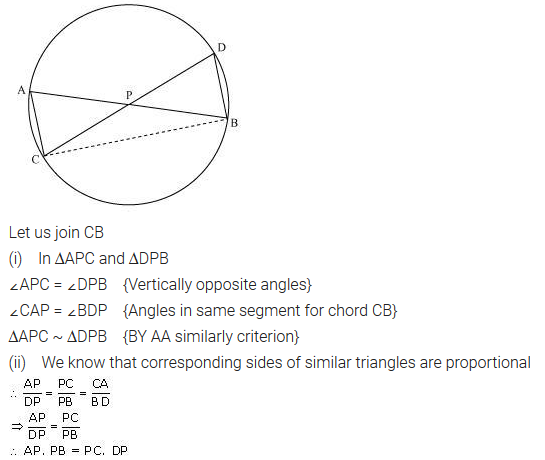

Ex 6.6 Class 10 Maths Question 8.
In the given figure, two chords Ab and CD of a circle intersect each other at the point P (when produced) outside the circle. Prove that:
(i) ∆PAC ~ ∆PDB
(ii)PA X PB = PC X PD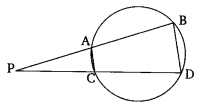

Solution:

Ex 6.6 Class 10 Maths Question 9.
In the given figure, D is a point on side BC of ∆ABC, such that 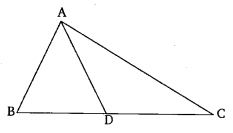BDCD=ABAC∙ Prove that AD is the bisector of ∆BAC.

Solution: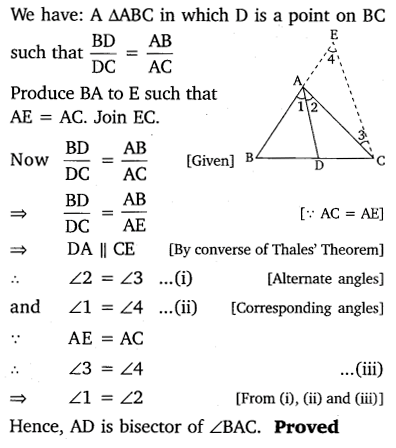

Ex 6.6 Class 10 Maths Question 10.
Nazima is fly fishing in a stream. The trip of her fishing rod is 1.8m above the surface of the water and the fly at the end of the string rests on the water 3.6m away and 2.4 m from a point directly under the trip of the rod. Assuming that her string (from the trip of the rod to the fly) is that, how much string does she have out (see the figure)? If she pills in the string at the rate of 5 cm per second, what will be the horizontal distance of the fly from her after 12 seconds?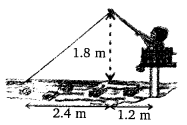

Solution:

NCERT Solutions For Class 10 Maths Chapter 6 Triangles Ex 6.1 in Hindi Medium

प्र. 1. कोष्ठकों में दिए शब्दों में से सही शब्दों का प्रयोग करते हुए, रिक्त स्थानों को भरिए :
(i) सभी वृत्त …….. होते है| (सर्वांगसम, समरूप)
(ii) सभी वर्ग…… होते हैं| (समरूप, सर्वांगसम)
(iii) सभी …….. त्रिभुज समरूप होते है | (समद्विबाहु, समबाहु)
(iv) भुजाओं की समान संख्या वाले दो बहुभुज समरूप होते हैं, यदि
(i) उनके संगत कोण ……..हो तथा
(ii) उनकी संगत ……भुजाएँ हों| (बराबर, समानुपाती|
हलः
(i) सभी वृत्त समरूप होते हैं।
(ii) सभी वर्ग समरूप होते हैं।
(iii) सभी समबाहु त्रिभुज समरूप होते हैं।
(iv) भुजाओं की समान संख्या वाले दो बहुभुजे समरूप होते हैं, यदि
(i) उनके संगत कोण बराबर हों तथा
(ii) उनकी संगत समानुपाती भुजाएँ हों।

प्र० 2. निम्नलिखित युग्मों के दो भिन्न-भिन्न उदाहरण दीजिएः
(i) समरूप आकृतियाँ
(ii) ऐसी आकृतियाँ जो समरूप नहीं हैं।
हलः
(i) (a) दो वृत्त परस्पर समरूप होते हैं।
(b) दो वर्ग परस्पर समरूप होते हैं।
(ii) (a) एक वृत्त और एक त्रिभुज समरूप नहीं होते हैं।
(b) एक समद्विबाहु त्रिभुज और एक विषमबाहु। त्रिभुज समरूप आकृतियाँ नहीं होती हैं।

प्र० 3. बताइए कि निम्न चतुर्भुज समरूप हैं या नहीं:

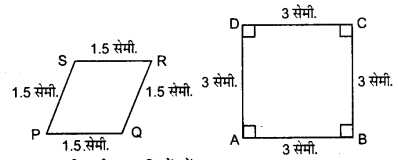
हलः 

संगत भुजाएँ समानुपाती हैं, परन्तु इनके संगत कोण समान नहीं हैं। ये आकृतियाँ समरूप नहीं हैं।

Class 10 Maths Triangles Mind Map

Similar Figures

Two figures having the same shape but not necessarily the same size are called similar figures
Two figures having the same shape as well as same size are called congruent figures
Note that all congruent figures are similar but the similar figures need not be congruent.

Similarity of Polygons

Two polygons of the same number of sides are similar if
(i) their corresponding angles are equal and
(ii) their corresponding sides are in the same ratio (or proportion)

Similarity of Triangles

Two triangles are similar if
(i) their corresponding angles are equal and
(ii) their corresponding sides are in the same ratio (or proportion)
Note : If the corresponding angles of two triangles are equal, then they are known as equiangular triangles.
The ratio of any two corresponding sides in two equiangular triangles is always the same.

Basic Proportionality Theorem (BPT) and its Converse

Basic Proportionality Theorem
If a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, then other two sides are divided in the same ratio. Thus in ∆ABC, if DE || BC, then

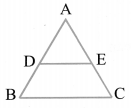
Converse of BPT
If a line divides any two sides of a triangle in the same ratio, then the line is parallel to the third side,

Criteria For Similarity of Triangles

(i) AAA Similarity Criterion : If in two triangles, corresponding angles are equal then their corresponding sides are in the same ratio and hence the two triangles are similar.
(ii) AA Similarity Criterion : If in two triangles, two angles of one triangle are respectively equal to the two angles of the other triangle, then the two triangles are similar.
(iii) SSS Similarity Criterion : If in two triangles, corresponding sides are in the same ratio then their corresponding angles are equal and hence the triangles are similar.
(iv) SAS Similarity Criterion : If one angle of a triangle is equal to one angle of another triangle and the sides including these angles are in the same ratio (proportion), then the two triangles are similar.

Areas of Similar Triangles

The ratio of the area of two similar triangles is equal to the ratio of the squares for their corresponding sides thus if ∆ABC – ∆PQR, then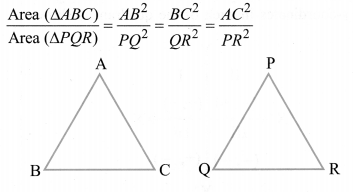

Pythagoras Theorem and its Converse

(i) If perpendicular is drawn from the vertex of the right angle of a right triangle to the hypotenuse then the triangles on both sides of the perpendicular are similar to the whole triangle and also to each other.
(ii) Pythagoras Theorem : In a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides. Thus in right ∆ABC right angled at B
AC2 = AB2 + BC2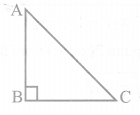

(iii) Converse of Pythagoras Theorem : If in a triangle, square of one side is equal to the sum of the squares of the other two sides, then the angle opposite the first side is a right angle.

Class 10 Maths Notes Chapter 6 Triangles

SIMILAR FIGURES

• Two figures having the same shape but not necessary the same size are called similar figures.
• All congruent figures are similar but all similar figures are not congruent.

SIMILAR POLYGONS
Two polygons are said to be similar to each other, if:
(i) their corresponding angles are equal, and
(ii) the lengths of their corresponding sides are proportional

Example:
Any two line segments are similar since length are proportional

Any two circles are similar since radii are proportional

Any two squares are similar since corresponding angles are equal and lengths are proportional.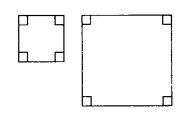

Note:
Similar figures are congruent if there is one to one correspondence between the figures.
∴ From above we deduce:

Any two triangles are similar, if their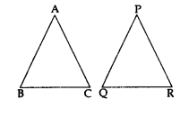

(i) Corresponding angles are equal
∠A = ∠P
∠B = ∠Q
∠C = ∠R

(ii) Corresponding sides are proportional
ABPQ=ACPR=BCQR

THALES THEOREM OR BASIC PROPORTIONALITY THEORY

Theorem 1:
State and prove Thales’ Theorem.
Statement:
If a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, the other two sides are divided in the same ratio.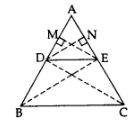

Given: In ∆ABC, DE || BC.
To prove: ADDB=AEEC
Const.: Draw EM ⊥ AD and DN ⊥ AE. Join B to E and C to D.
Proof: In ∆ADE and ∆BDE,
ar(ΔADE)ar(ΔBDE)=12×AD×EM12×DB×EM=ADDB ……..(i) [Area of ∆ = 12 x base x corresponding altitude
In ∆ADE and ∆CDE,
ar(ΔADE)ar(ΔCDE)=12×AE×DN12×EC×DN=AEEC
∵ DE || BC …[Given
∴ ar(∆BDE) = ar(∆CDE)
…[∵ As on the same base and between the same parallel sides are equal in area
From (i), (ii) and (iii),
ADDB=AEEC

CRITERION FOR SIMILARITY OF TRIANGLES

Two triangles are similar if either of the following three criterion’s are satisfied:

• AAA similarity Criterion. If two triangles are equiangular, then they are similar.
• Corollary(AA similarity). If two angles of one triangle are respectively equal to two angles of another triangle, then the two triangles are similar.
• SSS Similarity Criterion. If the corresponding sides of two triangles are proportional, then they are similar.
• SAS Similarity Criterion. If in two triangles, one pair of corresponding sides are proportional and the included angles are equal, then the two triangles are similar.

Results in Similar Triangles based on Similarity Criterion:

1. Ratio of corresponding sides = Ratio of corresponding perimeters
2. Ratio of corresponding sides = Ratio of corresponding medians
3. Ratio of corresponding sides = Ratio of corresponding altitudes
4. Ratio of corresponding sides = Ratio of corresponding angle bisector segments.

AREA OF SIMILAR TRIANGLES

Theorem 2.
The ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides.
Given: ∆ABC ~ ∆DEF
To prove: ar(ΔABC)ar(ΔDEF)=AB2DE2=BC2EF2=AC2DF2
Const.: Draw AM ⊥ BC and DN ⊥ EF.
Proof: In ∆ABC and ∆DEF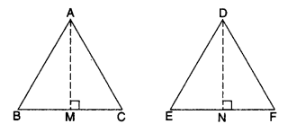

ar(ΔABC)ar(ΔDEF)=12×BC×AM12×EF×DN=BCEF.AMDN …(i) ……[Area of ∆ = 12 x base x corresponding altitude
∵ ∆ABC ~ ∆DEF
∴ ABDE=BCEF …..(ii) …[Sides are proportional
∠B = ∠E ……..[∵ ∆ABC ~ ∆DEF
∠M = ∠N …..[each 90°
∴ ∆ABM ~ ∆DEN …………[AA similarity
∴ ABDE=AMDN …..(iii) …[Sides are proportional
From (ii) and (iii), we have: BCEF=AMDN …(iv)
From (i) and (iv), we have: ar(ΔABC)ar(ΔDEF)=BCEF.BCEF=BC2EF2
Similarly, we can prove that
ar(ΔABC)ar(ΔDEF)=AB2DE2=AC2DF2
∴ar(ΔABC)ar(ΔDEF)=AB2DE2=BC2EF2=AC2DF2

Results based on Area Theorem:

1. Ratio of areas of two similar triangles = Ratio of squares of corresponding altitudes
2. Ratio of areas of two similar triangles = Ratio of squares of corresponding medians
3. Ratio of areas of two similar triangles = Ratio of squares of corresponding angle bisector segments.

Note:
If the areas of two similar triangles are equal, the triangles are congruent.

PYTHAGORAS THEOREM

Theorem 3:
State and prove Pythagoras’ Theorem.
Statement:
Prove that, in a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
Given: ∆ABC is a right triangle right-angled at B.
To prove: AB² + BC² = AC²
Const.: Draw BD ⊥ AC
Proof: In ∆s ABC and ADB,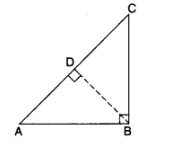

∠A = ∠A …[common
∠ABC = ∠ADB …[each 90°
∴ ∆ABC ~ ∆ADB …[AA Similarity
∴ ABAD=ACAB ………[sides are proportional]
⇒ AB² = AC.AD
Now in ∆ABC and ∆BDC
∠C = ∠C …..[common]
∠ABC = ∠BDC ….[each 90°]
∴ ∆ABC ~ ∆BDC …..[AA similarity]
∴ BCDC=ACBC ……..[sides are proportional]
BC² = AC.DC …(ii)
On adding (i) and (ii), we get
AB² + BC² = ACAD + AC.DC
⇒ AB² + BC² = AC.(AD + DC)
AB² + BC² = AC.AC
∴AB² + BC² = AC²

CONVERSE OF PYTHAGORAS THEOREM

Theorem 4:
State and prove the converse of Pythagoras’ Theorem.
Statement:
Prove that, in a triangle, if square of one side is equal to the sum of the squares of the other two sides, then the angle opposite the first side is a right angle.

Given: In ∆ABC, AB² + BC² = AC²
To prove: ∠ABC = 90°
Const.: Draw a right angled ∆DEF in which DE = AB and EF = BC
Proof: In ∆ABC,
AB² + BC² = AC² …(i) [given]
In rt. ∆DEF
DE² + EF² = DF² …[by pythagoras theorem]
AB² + BC² = DF² …..(ii) …[DE = AB, EF = BC]
From (i) and (ii), we get
AC² = DF²
⇒ AC = DF
Now, DE = AB …[by cont]
EF = BC …[by cont]
DF = AC …….[proved above]
∴ ∆DEF ≅ ∆ABC ……[sss congruence]
∴ ∠DEF = ∠ABC …..[CPCT]
∠DEF = 90° …[by cont]
∴ ∠ABC = 90°

Results based on Pythagoras’ Theorem:
(i) Result on obtuse Triangles.
If ∆ABC is an obtuse angled triangle, obtuse angled at B,
If AD ⊥ CB, then
AC² = AB² + BC² + 2 BC.BD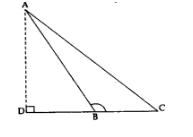

(ii) Result on Acute Triangles.
If ∆ABC is an acute angled triangle, acute angled at B, and AD ⊥ BC, then
AC² = AB² + BC² – 2 BD.BC.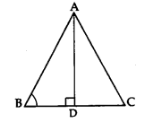

Exemplar Class 10 Maths Chapter 6 Triangles

NCERT Exemplar Class 10 Maths Chapter 6 Exercise 6.1

Choose the correct answer from the given four options:

Question 1.
In the figure, if ∠BAC = 90° and AD ⊥ BC. Then,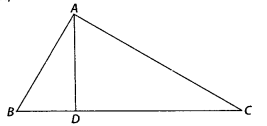

(A) BD . CD = BC2
(B) AB . AC = BC2
(C) BD . CD = AD2
(D) AB . AC = AD2
Solution:
(C)
In ∆ABC,
∠B + ∠BAC + ∠C = 180°
⇒ ∠B + 90° + ∠C = 180°
⇒ ∠B = 90° – ∠C
Similarly, In ∆ADC, ∠D AC = 90° – ∠C
In ∆ADB and ∆ADC,
∠D = ∠D = 90°
∠DBA = ∠D AC [each equal to (90° – ∠C)
∴ ∆ADB ~ ∆CDA
[by AA similarity criterion]
∴ BDAD=ADCD
⇒ BD . CD = AD2

Question 2.
The lengths of the diagonals of a rhombus are 16 cm and 12 cm. Then, the length of the side of the rhombus is
(A) 9 cm
(B) 10 cm
(C) 8 cm
(D) 20 cm
Solution:
(B)
We know that the diagonals of a rhombus are perpendicular bisectors of each other.
Given, AC = 16 cm and BD = 12 cm
∴ AO = 8 cm, BO = 6 cm and ∠AOB = 90°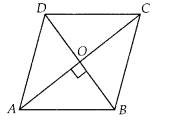

In right angled ∆AOB,
AB2 = AO2 + OB2 [by Pythagoras theorem]
⇒ AB2 = 82 + 62 = 64 + 36 = 100
∴ AB = 10 cm

Question 3.
If ∆ABC ~ ∆EDFand ∆ABC is not similar to ∆DEF, then which of the following is not true?
(A) BC . EF = AC . FD
(B) AB . EF = AC . DE
(C) BC . DE = AB . EF
(D) BC . DE = AB . FD
Solution:
(C)
Given, ∆ABC ~ ∆EDF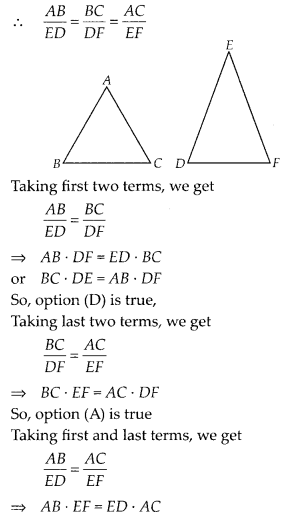

Hence, option (B) is true.

Question 4.
If in two triangles ABC and PQR, ABQR=BCPR=CAPQ then
(A) ∆PQR ~ ∆CAB
(B) ∆PQR ~ ∆ABC
(C) ∆CBA ~ ∆PQR
(D) ∆BCA ~ ∆PQR
Solution:
(A)
Given, in triangles ABC and PQR,
ABQR=BCPR=CAPQ
which shows that sides of one triangle are proportional to the sides of the other triangle, then their corresponding angles are also equal, so by SSS similarity, triangles are similar i.e., ∆CAB ~ ∆PQR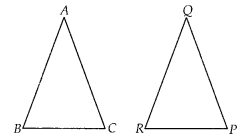

Question 5.
In the figure, two line segments AC and BD intersect each other at the point P such that PA = 6 cm, PB = 3 cm, PC = 2.5 cm, PD = 5 cm, ∠APB = 50° and ∠CDP = 30°. Then, ∠ PBA is equal to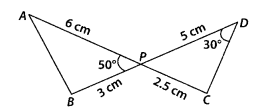

(A) 50°
(B) 30°
(C) 60°
(D) 100°
Solution:
(D): In ∆APB and ∆CPD, ∠APB = ∠CPD = 50°
[vertically opposite angles]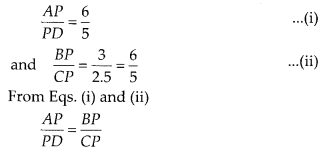

∴ ∆APB ~ ∆DPC [by SAS similarity criterion]
∴ ∠A = ∠D = 30° [corresponding angles of similar triangles]
In ∆APB, ∠A + ∠B + ∠APB = 180° [sum of angles of a triangle = 180°]
⇒ 30° + ∠B + 50° = 180°
∴ ∠B = 180° – (50° + 30°) = 100°
i.e., ∠PBA = 100°

Question 6.
If in two triangles DEF and PQR, ∠D = ∠Q and ∠R = ∠E, then which of the following is not true?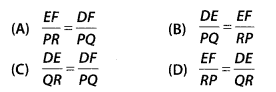

Solution:
(B)
Given, in ∆DEF and ∆PQR, ∠D = ∠Q, ∠R = ∠E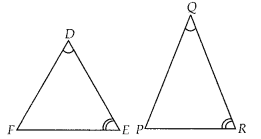

∴ ∆DEF ~ ∆QRP            [by AAA similarity criterion]
⇒ ∠F = ∠P
[corresponding angles of similar triangles]
∴DFQP=EDRQ=FEPR

Question 7.
In ∆ABC and ∆DEF, ∠B = ∠E, ∠F = ∠C and AB = 3 DE. Then, the two triangles are
(A) congruent but not similar
(B) similar but not congruent
(C) neither congruent nor similar
(D) congruent as well as similar
Solution:
(B)
In ∆ABC and ∆DEF, ∠B = ∠E,
∠F = ∠C and AB = 3DE

We know that, if in two triangles corresponding two angles are same, then they are similar by AA similarity criterion.
Since, AB ≠ DE
Therefore ∆ABC and ∆DEF are not congruent.

Question 8.
It is given that ∆ABC ~ ∆PQR with BCQR=13 then ar(ΔPRQ)ar(ΔBCA) equal to
(A) 9
(B) 3
(C) 13
(D) 19
Solution:
(A)
Given, ∆ABC ~ ∆QR and BCQR=13
We know that, the ratio of the areas of two similar triangles is equal to square of the ratio of their corresponding sides.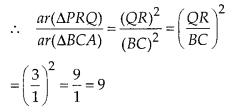

Question 9.
It is given that ∆ABC ~ ∆DFE, ∠A =30°, ∠C = 50°, AB = 5 cm, AC = 8 cm and DF= 7.5 cm. Then, the following is true:
(A) DE= 12 cm, ∠F= 50°
(B) DE= 12 cm, ∠F= 100°
(C) EF= 12 cm, ∠D = 100°
(D) EF= 12 cm, ∠D = 30°
Solution:
(B)
Given, ∆ABC ~ ∆DFE, then ∠A = ∠D = 30°, ∠C = ∠E = 50°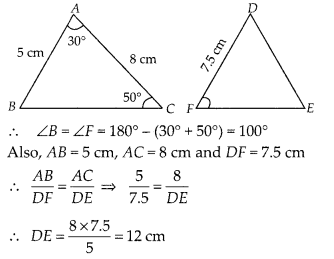

Hence, DE = 12 cm, ∠F = 100°

Question 10.
If in ∆ABC and ∆DEF, ABDE=BCFD, then they will be similar, when
(A) ∠B = ∠E
(B) ∠A = ∠D
(C) ∠B = ∠D
(D) ∠A = ∠F
Solution:
(C)
Given, in ∆ABC and ∆EDF,

So, ∆ABC ~ ∆EDF if ∠B = ∠D [By SAS similarity criterion]

Question 11.
If ∆ABC ~ ∆QRP, ar(ΔABC)ar(ΔPQR)=94, AB= 18 cm and BC = 15 cm, then PR is equal to
(A) 10 cm
(B) 12 cm
(C) 203 cm
(D) 8 cm
Solution:
(A)
Given, ∆ABC ~ ∆QRP, AB = 18 cm and BC = 15 cm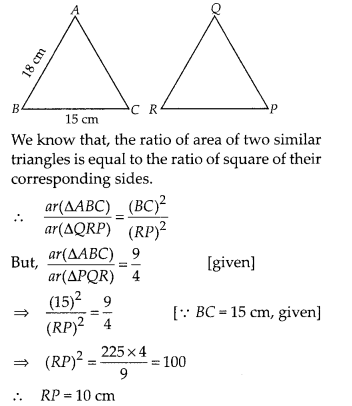

Question 12.
If S is a point on side PQ of a ∆PQR such that PS = QS = RS, then
(A) PR – QR = RS2
(B) QS2 + RS2 = QR2
(C) PR2 + QR2 = PQ2
(D) PS2 + RS2 = PR2
Solution:
(C)
Given, in ∆PQR,
PS = QS = RS …………. (i)
In ∆PSR, PS = RS [from Eq(i)]
⇒ ∠1 = ∠2 ………… (ii)
[Angles opposite to equal sides are equal]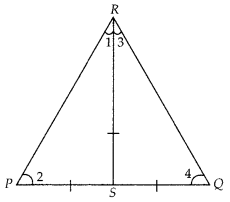

Similarly, in ∆RSQ, RS = SQ
⇒ ∠3 = ∠4 …………. (iii)
[angles opposite to equal sides are equal]
Now, in ∆PQR, sum of angles = 180°
⇒ ∠P + ∠Q + ∠P = 180°
⇒ ∠2 + ∠4 + ∠1 + ∠3 = 180°
⇒ ∠1 + ∠3 + ∠1 + ∠3 = 180°
⇒ 2(∠1 + ∠3) = 180°
⇒ ∠l + ∠3 = 180∘2 = 90°
∴ ∠R = 90°
In ∆PQR, by Pythagoras theorem,
PR2 + QR2 = PQ2

NCERT Exemplar Class 10 Maths Chapter 6 Exercise – 6.2

Question 1.
Is the triangle with sides 25 cm, 5 cm and 24 cm a right triangle? Give reasons for your answer.
Solution:
False
Let a = 25 cm, b = 5 cm and c = 24 cm
Now, b2 + c2 = (5)2 + (24)2
= 25 + 576 = 601 ≠ (25)2
Hence, given sides do not make a right triangle because it does not satisfy the property of Pythagoras theorem.

Question 2.
It is given that ∆DEF ~ ∆RPQ. Is it true to say that ∠D = ∠R and ∠F = ∠P? Why?
Solution:
False
We know that, if two triangles are similar, then their corresponding angles are equal.
∴ ∠D = ∠R, ∠E = ∠P and ∠F = Q

Question 3.
A and B are respectively the points on the sides PQ and PR of A PQR such that PQ = 12.5 cm, PA = 5 cm, BR = 6 cm and PB = 4 cm. Is 4B||Q/?? Give reasons for your answer.
Solution:
True
Given, PQ = 12.5 cm, PA = 5 cm, BR = 6 cm and PB = 4 cm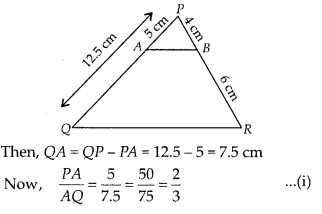

and PBBR=46=23
From Eqs. (i) and (ii), PAAQ=PBBR
By converse of basic proportionality theorem, AB || QR

Question 4.
In the figure, BD and CE intersect each other at the point P. Is A∆PBC ~ ∆PDE?Why?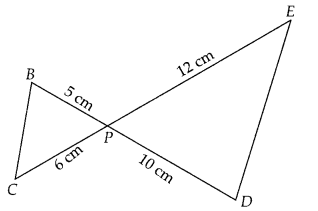

Solution:
True
In ∆PBC and ∆PDE,
∠BPC = ∠EPD [vertically opposite angles]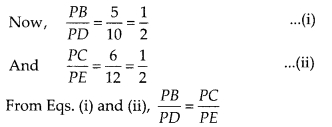

Since, one angle of ∆PBC is equal to one angle of ∆PDE and the sides including these angles are proportional, so both triangles are similar.
Hence, ∆PBC ~ ∆PDE, by SAS similarity criterion.

Question 5.
In ∆PQR and ∆MST, ∠P = 55°, ∠Q = 25°, ∠M = 100° and ∠S = 25°. Is ∆QPR ~ ∆TSM? Why?
Solution:
False
We know that, the sum of three angles of a triangle is 180°.
In ∆PQR, ∠P +∠Q +∠R = 180°
⇒ 55° + 25 ° + ∠R = 180°
⇒∠R = 180° – (55° + 25 °)
= 180° – 80° = 100°
In ∆TSM, ∠T + ∠S + ∠M = 180°
⇒ ∠T + ∠25° + 100° = 180°
⇒ ∠T = 180° – (25° + 100°) = 180° – 125° = 55°

In ∆PQR and ∆TSM,
∠P = ∠T, ∠Q = ∠S and ∠R = ∠M
∴ ∠PQR = ∠TSM
[since, all corresponding angles are equal]
Hence, ∆QPR is not similar to ∆TSM, since correct correspondence is P ↔ T, Q ↔ S and R ↔ M.

Question 6.
Is the following statement true? Why? “Two quadrilaterals are similar, if their corresponding angles are equal”.
Solution:
False
Two quadrilaterals are similar if their corresponding angles are equal and corresponding sides must also be proportional.

Question 7.
Two sides and the perimeter of one triangle are respectively three times the corresponding sides and the perimeter of the other triangle. Are the two triangles similar? Why?
Solution:
True
Here, the corresponding two sides and the perimeters of two triangles are proportional, then the third side of both triangles will also in proportion.

Question 8.
If in two right triangles, one of the acute angles of one triangle is equal to an acute angle of the other triangle, can you say that the two triangles will be similar? Why?
Solution:
True
Let two right angled triangles be ∆ABC and ∆PQR

In which, ∠A = ∠P = 90° and ∠B = ∠Q = acute angle (Given)
Then, by AA similarity criterion, ∆ABC ~ ∆PQR

Question 9.
The ratio of the corresponding altitudes of two similar triangles is 35.Is it correct to say that ratio of their areas is 65 ? Why?
Solution:
False
Ratio of corresponding altitudes of two triangles having areas A1 and A2 respectively is 35.
By the property of area of two similar triangles,
⇒(A1A2)=(35)2⇒925≠65
So, the given statement is not correct.

Question 10.
D is a point on side QR of ∆PQR such that PD ⊥ QR. Will it be correct to say that ∆PQD ~ A∆RPD? Why?
Solution:
False
In ∆PQD and ∆RPD,
PD = PD [common side]
∠PDQ = ∠PDR [each 90°]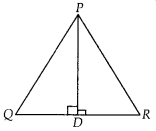

Here, no other sides or angles are equal, so we can say that ∆PQD is not similar to ∆RPD. But if ∠P = 90°, then ∠DPQ = ∠PRD
[each equal to 90° – ∠Q and by ASA similarity criterion, ∆PQD ~ ∆RPD]

Question 11.
In the figure, if ∠D = ∠C, then is it true that ∆ADE ~ ∆ACB? Why?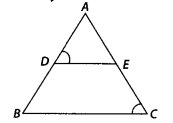

Solution:
True
In ∆ADE and ∆ACB,
∠A = ∠A [common angle]
∠D = ∠C [given]
∴ ∆ADE ~ ∆ACB [by AA similarity criterion]

Question 12.
Is it true to say that if in two triangles, an angle of one triangle is equal to an angle of another triangle and two sides of one triangle are proportional to the two sides of the other triangle, then the triangles are similar? Give reasons for your answer.
Solution:
False
Because, according to SAS similarity criterion, if one angle of a triangle is equal to an angle of the other triangle and the sides including these angles are proportional, then the two triangles are similar.
Here, one angle and two sides of two triangles are equal but these sides not including equal angle, so given statement is not correct.

NCERT Exemplar Class 10 Maths Chapter 6 Exercise – 6.3

Question 1.
In a ∆PQR, PR2 – PQ2 = QR2 and M is a point on side PR such that QM⊥ PR. Prove that QM2 = PM × MR.
Solution:
Given, In ∆PQR,
PR2 – PQ2 = QR2 and QM ⊥ PR
To prove : QM2 = PM × MR
Proof : Since, PR2 – PQ2 = QR2
⇒ PR2 = PQ2 + QR2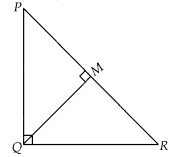

So, ∆PQR is right angled triangle right angle at Q.
In ∆QMR and ∆PMQ, ∠M = ∠M [each 90°]
∠MQR = ∠QPM [each equal to 90° – ∠R]
∴ ∆QMR ~ ∆PMQ [by AA similarity criterion]
Now, using property of area of similar triangles, we get

Question 2.
Find the value of x for which DE || AB is given figure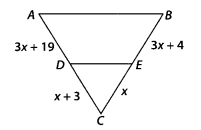

Solution:
Given, DE || AB
∴ CDAD=CEBE [by basic proportionality theorem]
x+33x+19=x3x+4
⇒ (x + 3)(3x + 4) = x (3x + 19)
⇒ 3x2 + 4x + 9x + 12 = 3x2 + 19x
⇒ 19x – 13x = 12
⇒ 6x = 12
∴ x = 126 = 2
Hence, the required value of x is 2.

Question 3.
In the figure, if ∠1 = ∠2and ∆NSQ ≅ ∆MTR, then prove that ∆PTS ~ ∆PRQ.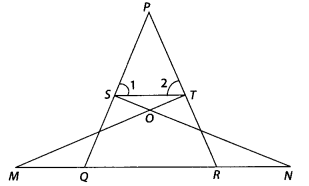

Solution:
Given ∆NSQ ≅ ∆MTR and ∠1 = ∠2
To prove : ∆PTS ~ ∆PRQ
Proof : Since, ∆NSQ ≅ ∆MTR
So, SQ = TR ………….. (i)
Also, ∠1 = ∠2 ⇒ PT = PS ………… (ii)
[since, sides opposite to equal angles are also equal]
From Eqs.(i) and (ii), PSSQ=PTTR
⇒ ST || QR            [by converse of basic proportionality theorem]
∴ ∠1 = ∠PQR          [Corresponding angles]
and ∠2 = ∠PRQ
In ∆PTS and ∆PRQ,
∠P = ∠P [common angles]
∠1 = ∠PQR
∠2 = ∠PRQ
∴ ∆PTS ~ ∆PRQ              [by AAA similarity criterion]

Question 4.
Diagonals of a trapezium PQRS intersect each other at the point O, PQ || RS and PQ = 3 RS. Find the ratio of the areas of ∆POQ and ∆ROS.
Solution:
Given PQRS is a trapezium in which PQ || RS and PQ = 3RS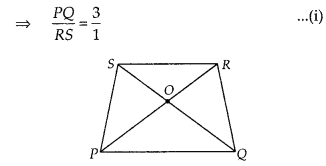

In ∆POQ and ∆ROS,
∠SOR = ∠QOP     [vertically opposite angles]
∠SRP = ∠RPQ     [alternate angles]
∴ ∆POQ ~ ∆ROS       [by AA similarity criterion]
By property of area of similar triangles,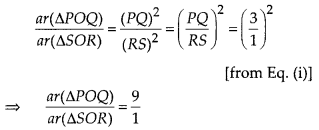

Hence, the required ratio is 9 : 1

Question 5.
In the figure if AB || DC and AC and PQ intersect each other at the point O, prove that OA . CQ = OC . AP.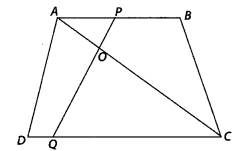

Solution:
Given AC an PQ intersect each other at point O and AB || DC
To prove : OA . CQ = OC . AP
Proof: In ∆AOP and ∆COQ,
∠AOP = ∠COQ [vertically opposite angles]
∠APO = ∠CQO
[since AB || DC and PQ is transversal, so alternate angles]
∴ ∆AOP ~ ∆COQ          [by AA similarity criterion]
Then, OAOC=APCQ
[since, corresponding sides are proportional]
⇒ OA . CQ = OC . AP Hence proved.

Question 6.
Find the altitude of an equilateral triangle of side 8 cm.
Solution:
Let ABC be an equilateral triangle of side 8 cm i.e., AB = BC = CA = 8 cm
Draw altitude AD which is perpendicular to BC. Then, D is the mid-point of BC.
∴ BD = CD = 12 BC = 82 = 4 cm
Now, AB2 = AD2 + BD2 [by Pythagoras theorem]

⇒ (8)2 = AD2 + (4)2
⇒ 64 = AD2 + 16
⇒ AD2 = 64 – 16 = 48
⇒ AD = 48−−√ = 43–√ cm
Hence, altitude of an equilateral triangle is 43–√ cm

Question 7.
If ∆ABC ~ ∆DEF, AB = 4 cm, DE = 6 cm, EF = 9 cm and FD = 12 cm, find the perimeter of ∆ABC.
Solution:
Given AB = 4 cm, DE = 6 cm and EF = 9 cm and FD = 12 cm
Also, ∆ABC ~ ∆DEF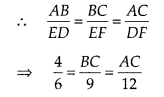


Now, perimeter of ∆ABC = AB + BC + AC = 4 + 6 + 8 = 18 cm

Question 8.
In the figure, if DE || BC, find the ratio of ar(∆ADE) and ar(∆ECB).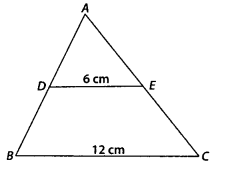

Solution:
Given, DE || BC, DE = 6 cm and BC = 12 cm
In ∆ABC and ∆ADE,
∠ABC = ∠ADE         [corresponding angle]
and ∠A = ∠A         [common side]
∴ ∆ABC ~ ∆ADE          [by AA similarity criterion]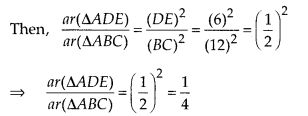

Let ar(∆ADE) = k, then ar(∆ABC) = 4k
Now, ar(∆ECB) = ar(ABC) – ar(ADE) = 4k – k = 3k
∴ Required ratio = ar(ADE): ar(DECB)
= k : 3k = 1 : 3

Question 9.
ABCD is a trapezium in which AB || DC and P, Q are points on AD and BC, respectively such that PQ || DC. If PD = 18 cm, BQ = 35 cm and QC = 15 cm, find AD.
Solution:
Given, a trapezium ABCD in which AB || DC. P and Q are points on AD and BC, respectively such that PQ || DC. Thus,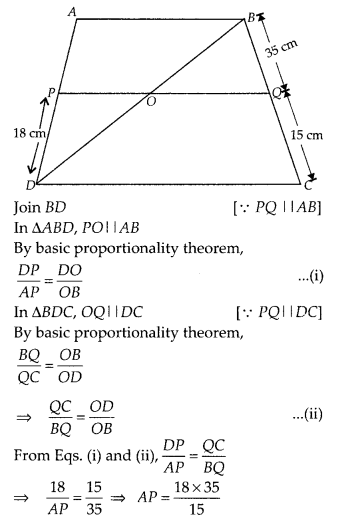 
⇒ AP = 42 cm.
Now; AD = AP + PD = 42 + 18 = 60
∴ AD = 60 cm

Question 10.
Corresponding sides of two similar triangles are in the ratio of 2 : 3. If the area of the smaller triangle is 48 cm2, find the area of the larger triangle.
Solution:
Given, ratio of corresponding sides of two similar triangles is 2 : 3 or 23
Area of smaller triangle = 48 cm2
By the property of area of two similar triangles,
Ratio of area of both triangles = (Ratio of their corresponding sides)2

Question 11.
In a ∆PQR, N is a point on PR, such that QN ⊥ PR. If PN . NR = QN2, prove that ∠PQR = 90°
Solution:
Given, ∆PQR, N is a point on PR, such that QN ⊥ PR and PN . NR = QN2
To prove : ∠PQR = 90°
Proof: We have, PN . NR = QNc
⇒ PN . NR = QN . QN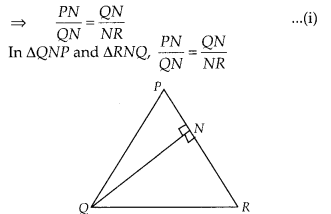

and ∠PNQ = ∠RNQ [each equal to 90° ]
∴ ∆QNP ~ ∆RNQ        [by SAS similarity criterion]
Then, ∆QNP and ∆RNQ are equiangulars.
i.e., ∠PQN = ∠QRN
⇒ ∠RQN-∠QPN
On adding both sides, we get
∠PQN + ∠RQN = ∠QRN + ∠QPN
⇒ ∠PQR = ∠QRN + ∠QPN …………… (ii)
We know that, sum of angles of a triangle is 180°
In ∆PQR, ∠PQR + ∠QPR + ∠QRP = 180°
⇒ ∠PQR + ∠QPN + ∠QRN = 180°
[ ∵∠QPR = ∠QPN and ∠QRP = ∠QRN]
⇒ ∠PQR + ∠PQR = 180° [using Eq. (ii)]
⇒ 2∠PQR = 180°
⇒ ∠PQR = 180∘2 = 90°
∴ ∠PQR = 90° Hence proved.

Question 12.
Areas of two similar triangles are 36 cm2 and 100 cm2 . If the length of a side of the larger triangle is 20 cm, find the length of the corresponding side of the smaller triangle.
Solution:
Given, area of smaller triangle = 36 cm2
and area of larger triangle= 100 cm2
Also, length of a side of the larger triangle = 20 cm
Let length of the corresponding side of the smaller triangle = x cm
By property of area of similar triangles,

Question 13.
In the figure, if ∠ACB = ∠CDA, AC = 8 cm and AD = 3 cm, find BD.

Solution:
Given, AC = 8 cm, AD = 3 cm
and ∠ACB = ∠CDA
In ∆ACD and ∆ABC,
∠A = ∠A       [Common angle]
∠ADC = ∠ACB      [Given]
∴ ∆ADC ~ ∆ACB      [By AA similarity criterion]

Question 14.
A 15 metres high tower casts a shadow 24 metres long at a certain time and at the same time, a telephone pole casts a shadow 16 metres long. Find the height of the telephone pole.
Solution:
Let BC = 15 m be the tower and its shadow AB is 24 m. At that time ∠CAB = θ. Again, let EF = h be a telephone pole and its shadow DE = 16 m. At the same time ∠EDF = θ. Here, ∆ABC and ∆DEF both are right angled triangles.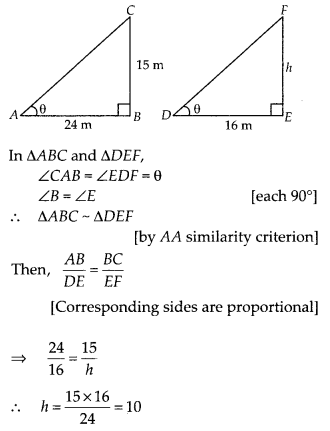

Hence, the height of the point on the wall where the top of the ladder reaches is 8 m.

Question 15.
Foot of a 10 m long ladder leaning against a vertical wall is 6 m away from the base of the wall. Find the height of the point on the wall where the top of the ladder reaches.
Solution:
Let AB be a vertical wall and AC = 10 m is a ladder. The top of the ladder reached to A and distance of ladder from the base of the wall BC is 6 m.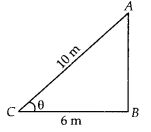

In right angled ∆ABC
AC2 = AB2 + BC2 [by Pythagoras theorem]
⇒ (10)2 = AB2 + (6)2
⇒ 100 = AB2 + 36
⇒ AB2 = 100 – 36 = 64
∴ AB = 64−−√ = 8 m
Hence the height of the point on th wall where the top of the ladder reaches is 8 m.

NCERT Exemplar Class 10 Maths Chapter 6 Exercise – 6.4

Question 1.
In the given figure, if ∠A = ∠C, AB = 6 cm, BP = 15 cm, AP = 12 cm and CP = 4 cm, then find the lengths of PD and CD.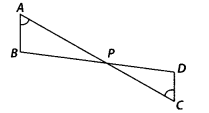

Solution:
Given ∠A = ∠C, AB = 6 cm, BP = 15 cm,
AP = 12 cm and CP = 4 cm
In ∆APB and ∆CPD,
∠A = ∠C [given]
∠APB = ∠CPD [vertically opposite angles]
∴ ∆APB ~ ∆CPD [by AA similarity criterion]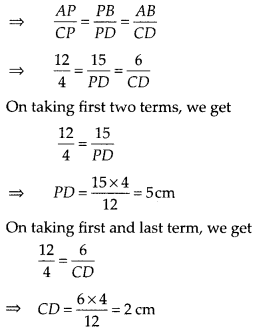

Hence, length of PD is 5 cm and length of CD is 2 cm.

Question 2.
It is given that ∆ABC ~ ∆EDF such that AB = 5 cm, AC = 7 cm, DF = 15 cm and DE = 12 cm. Find the lengths of the remaining sides of the triangles.
Solution:
Given, ∆ABC ~ ∆EDF, so the corresponding sides of ∆ABC and ∆EDF are in the same ratio
i.e., 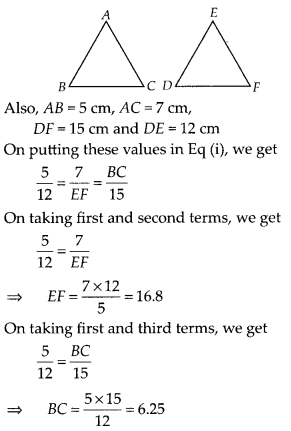ABED=ACEF=BCDF ………………. (i)

Hence, lengths of the remaining sides of the triangles are EF = 16.8 cm and BC = 6.25 cm.

Question 3.
Prove that if a line is drawn parallel to one side of a triangle to intersect the other two sides, then the two sides are divided in the same ratio.
Solution:
Let a ∆ABC in which a line DE parallel to BC intersects AB at D and AC at E.
To prove : DE divides the two sides in the same ratio.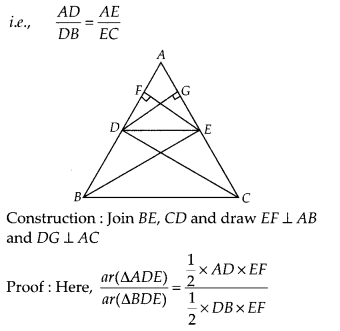


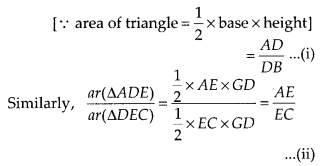
Now, since, ∆BDE and ∆DEC lie between the same parallel lines DE and BC and on the same base DE
So, ar(∆BDE) = ar(∆DEC) ………….. (iii)
From Eqs. (i), (ii) and (iii),
ADDB=AEEC
Hence proved

Question 4.
In the figure, if PQRS is a parallelogram and AB || PS, then prove that OC || SR.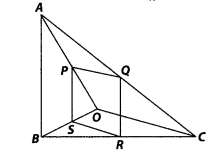

Solution:
Given PQRS is a parallelogram, so PQ || SR and PS || QR. Also AB || PS.
To prove : OC || SR
Proof : In ∆OPS and ∆OAB, PS || AB
∠POS = ∠AOB    [common angle]
∠OSP = ∠OBA        [corresponding angles]
∴ ∆OPS ~ ∆OAB           [by AA similarity criterion]
Then, PSAB=OSOB ………… (i)
In ∆CQE and ∆CAB, QR || PS || AB
∠QCR = ∠ACB [common angle]
∠CRQ = ∠CBA [corresponding angles]
∴ ∆CQR ~ ∆CAB

On subtracting 1 from both sides, we get OB CB

By converse of basic proportionality theorem, SR || OC.
Hence proved

Question 5.
A 5 m long ladder is placed leaning towards a vertical wall such that it reaches the wall at a point 4 m high. If the foot of the ladder is moved 1.6 m towards the wall, then find the distance by which the top of the ladder would slide upwards on the wall.
Solution:
Let AC be the ladder of length 5 m and BC = 4 m be the height of the wall, which ladder is placed. If the foot of the ladder is moved 1.6 m towards the wall i.e, AD = 1.6 m, then the ladder is slide upward i.e., CE = x m.
In right angled ∆ABC,
AC2 = AB2 + BC2     [by Pythagoras theorem]
⇒ (5)2 = (AB)2 + (4)2
⇒ AB2 = 25 – 16 = 9
⇒ AB = 3m
Now, DB = AB – AD = 3 – 1.6 = 1.4 m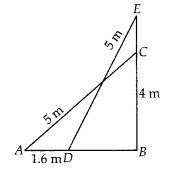

In right angled ∆EBD,
ED2 = EB2 + BD2       [by Pythagoras theorem]
⇒ (5)2 = (EB)2 + (1.4)2 [ ∵ BD = 1.4 m]
⇒ 25 = (EB)2 + 1.96
⇒ (EB)2 = 25 – 1.96 = 23.04
⇒ EB = 23.04−−−−√ = 4.8
Now, EC = EB – BC = 4.8 – 4 = 0.8
Hence, the top of the ladder would slide upwards on the wall at distance is 0.8 m.

Question 6.
For going to a city B from city A, there is a route via city C such that AC ⊥ CB, AC = 2x km and CB = 2 (x + 7) km. It is proposed to construct a 26 km highway which directly connects the two cities A and B. Find how much distance will be saved in reaching city B from city A after the construction of the highway.
Solution:
Given, AC ⊥ CB, AC = 2xkm,CB = 2(x + 7)km and AB = 26 km
On drawing the figure, we get the right angle ∆ACB right angled at C.
Now, In ∆ACB, by Pythagoras theorem,
AB2 = AC2 + BC2
⇒ (26)2 = (2x)2 + {2(x + 7)}2
⇒ 676 = 4x2 + 4(x2 + 49 + 11x)
⇒ 676 = 4x2 + 4x2 + 196 + 56x
⇒ 676 = 8x2 + 56x + 196
⇒ 8x2 + 56x – 480 = 0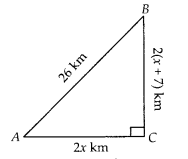

On dividing by 8, we get x2 + 7x – 60 = 0
⇒ x2 + 12x-5x-60 = 0
⇒ x(x + 12) – 5(x + 12) = 0
⇒ (x + 12)(x – 5) = 0
∴ x = -12, x = 5
Since, distance cannot be negative.
∴ x = 5 [∵ x ≠ 12]
Now, AC = 2x = 10 km and BC = 2(x + 7) = 2(5 + 7) = 24 km
The distance covered to reach city B from city A via city C = AC + BC = 10 + 24 = 34 km
Distance covered to reach city B from city A after the construction of the highway is
BA = 26 km
Hence, the required saved distance is 34 – 26
i.e., 8 km

Question 7.
A flag pole 18 m high casts a shadow 9.6 m long. Find the distance of the top of the pole from the far end of the shadow.
Solution:
Let BC = 18 m be the flag pole and its shadow be AB = 9.6 m. The distance of the top of the pole, C from the far end i.e., A of the shadow is AC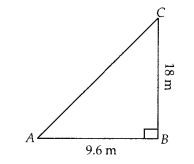

In right angled ∆ABC
AC2 = AB2 + BC2 [by Pythagoras theorem]
⇒ AC2 = (9.6)2 + (18)2
⇒ AC2 = 92.16 + 324
⇒ AC2 = 416.16
∴ AC = 416.16−−−−−√ = 20.4 m
Hence, the required distance is 20.4 m.

Question 8.
A street light bulb is fixed on a pole 6 m above the level of the street. If a woman of height 1.5 m casts a shadow of 3m, find how far she is away from the base of the pole.
Solution:
Let A be the position of the street bulb fixed on a pole AB = 6 m and CD = 1.5 m be the height of a woman and her shadow be ED = 3 m. Let distance between pole and woman be x m.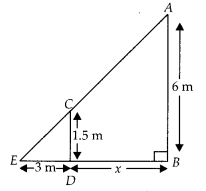

Here, woman and pole both are standing vertically
So, CD || AB
In ∆CDE and ∆ABE,
∠E = ∠E [common angle]
∠ABE = ∠CDE [each equal to 90°]
∴ ∆CDE ~ ∆ABE [by AA similarity criterion]
Then EDEB=CDAB⇒33+x=1.56
⇒ 3 × 6 = 1.5(3 + x)
⇒ 18 = 1.5 × 3 + 1.5x
⇒ 1.5x = 18 – 4.5
∴ x = 13.51.5 = 9 m
Hence, she is at the distance of 9 m from the base of the pole.

Question 9.
In the figure, ABC is a triangle right angled at B and BD ⊥ AC. If AD = 4 cm, and CD = 5 cm, find BD and AB.

Solution:
Given, ∆ABC in which ∠B = 90° and BD ⊥ AC
Also, AD = 4 cm and CD = 5 cm
In ∆DBA and ∆DCB,
∠ADB = ∠CDB [each equal to 90°]
and ∠BAD = ∠DBC [each equal to 90° – ∠C] ;.
∴ ∆DBA ~ ∆DCB [by AA similarity criterion]

Question 10.
In the figure, PQR is a right triangle right angled at Q and QS ⊥ PR. If PQ = 6 cm and PS = 4 cm, find QS, RS and QR.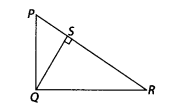

Solution:
Given, ∆PQR in which ∠Q = 90°, QS ⊥ PR and PQ = 6 cm, PS = 4 cm
In ∆SQP and ∆SRQ,
∠PSQ = ∠RSQ [each equal to 90°]
∠SPQ = ∠SQR [each equal to 90° – ∠R]
∴ ∆SQP ~ ∆SRQ [By AA similarity criterion]
Then, SQPS=SRSQ
⇒ SQ2 = PS × SR ………….. (i)
In right angled ∆PSQ,
PQ2 = PS2 + QS2 [by Pythagoras theorem]
⇒ (6)2 = (4)2.+ QS2
⇒ 36 = 16 + QS2
⇒ QS2 = 36 – 16 = 20
∴ QS.= 20−−√=25–√ cm
On putting the value of QS in Eq(i), we get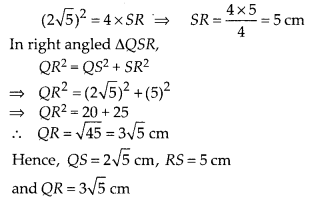

Question 11.
In ∆PQR, PD ⊥ QR such that D lies on QR . If PQ = a, PR = b, QD = c and DR = d, prove that [a + b)(a – b) = (c + d)(c – d).
Solution:
Given: In ∆PQR, PD ⊥ QR, PQ = a, PR = b,
QD = c and DR = d
To prove : (a + b)(a -b) = (c + d)(c – d)
Proof : In right angled ∆PDQ,
PQ2 = PD2 + QD2 [by Pythagoras theorem]
⇒ a2 = PD2 + c2
⇒ PD2 = a2 – c2 …………. (i)

In right angled ∆PDR,
PR2 = PD2 + DR2 [by Pythagoras theorem]
⇒ b2 = PD2 + d2
⇒ PD2 = b2 – d2 ………….. (ii)
From Eqs. (i) and (ii)
a2 – c2 = b2 – d2
⇒ a2 – b2 = c2 – d2
⇒ (a – b)(a + b) = (c – d)(c + d)
Hence proved.

Question 12.
In a quadrilateral ABCD, ∠A + ∠D = 90°. Prove that AC2 + BD2 = AD2 + BC2 [Hint: Produce AB and DC to meet at E]
Solution:
Given : Quadrilateral ABCD, in which ∠A + ∠D = 90°
To prove : AC2 + BD2 = AD2 + BC2
Construct: Produce AB and CD to meet at E
Also join AC and BD

Proof: In ∆AED, ∠A + ∠D = 90° [given]
∴ ∠E = 180° – (∠A + ∠D) = 90°
[ ∵ sum of angles of a triangle = 180°]
Then, by Pythagoras theorem,
AD2 = AE2 + DE2
In ∆BEC, by Pythagoras theorem,
BC2 = BE2 + EC2
On adding both equations, we get
AD2 + BC2 = AE2 + DE2 + BE2 + CE2 ………… (i)
In ∆AEC, by Pythagoras theorem,
AC2 = AE2 + CE2
and in ∆BED, by Pythagoras theorem,
BD2 = BE2 + DE2
On adding both equations, we get
AC2 + BD2 = AE2 + CE2 + BE2 + DE2 ………… (ii)
From Eqs. (i) and (ii)
AC2 + BD2 = AD2 + BC2
Hence proved.

Question 13.
In the given figure, l || m and line segments AB, CD and EF are concurrent at point P. Prove that 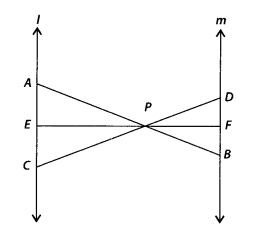AEBF=ACBD=CEFD

Solution:
Given l || m and line segments AB, CD and EF are concurrent at point P

Question 14.
In the figure, PA, QB, RC and SD are all perpendiculars to a line l,AB = 6 cm, BC = 9 cm, CD = 12 cm and SP = 36 cm. Find PQ,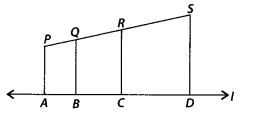

Solution:
Given, AB = 6 cm, BC = 9 cm, CD = 12 cm and SP = 36 cm
Also, PA, QB, RC and SD are all perpendiculars to line l
∴ PA || QB || RC || SD By Basic proportionality theorem,
PQ : QR : RS = AB : BC : CD = 6 : 9 : 12
Let PQ = 6x, QR = 9x and RS = 12x
Since, length of PS = 36 cm
∴ PQ + QR + RS = 36
⇒ 6x + 9x + 12x = 36
⇒ 27x = 36
∴ x = 3627=43
Now, PQ = 6x = 6 × 43 = 8 cm
QR = 9x = 9 × 43= 12 cm
and RS = 12x = 12 × 43 = 16 cm

Question 15.
O is the point of intersection of the diagonals AC and BD of a trapezium ABCD with AB || DC. Through 0, a line segment PQ is drawn parallel to AB meeting AD in P and BC in Q. Prove that PO = QO.
Solution:
Given ABCD is a trapezium. Diagonals AC and BD are intersect at O.
PQ || AB || DC
To prove : PO = QO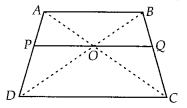

Proof : In ∆ABD and ∆POD, PO || AB [∵ PQ || AB]
∠D = ∠D [common angle]
∠ABD = ∠POD [corresponding angles]
∴ ∆ABD ~ ∆POD[by AA similarity criterion]
Then, OPAB=PDAD …………… (i)
In ∆ABC and ∆OQC, OQ || AB
∠C = ∠C [common angle]
∠B AC = ∠QOC [corresponding angles]
∴ ∆ABC ~ ∆OQC [by AA similarity criterion]

Question 16.
In the figure, line segment DF intersect the side AC of a ∆ABC at the point E such that E is the mid-point of CA and ∠AEF = ∠AFE. Prove that BDCD=BFCE
[Hint:Take point G on AB such that CG || DF]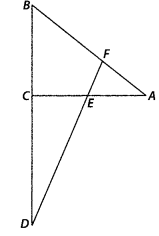

Solution:
Given ∆ABC, E is the mid-point of CA and ∠AEF = ∠AFE
To prove : BDCD=BFCE
Construction : Take a point G on AB such that CG || DF
Proof : Since, E is the mid-point of CA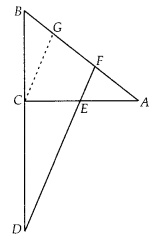

∴ CE = AE
In ∆ACG, CG || EF and E is mid-point of CA
So, CE = GF …………… (ii) [by mid-point theorem]
Now, in ∆BCG and ∆BDF, CG || DF

Question 17.
Prove that the area of the semicircle drawn on the hypotenuse of a right angled triangle is equal to the sum of the areas of the semicircles drawn on the other two sides of the triangle.
Solution:
Let ABC be a right triangle, right angled at B and AB = y, BC = x
Three semi-circles are drawn on the sides AB,
BC and AC, respectively with diameters AB,
BC and AC, respectively
Again, let area of circles with diameters AB,
BC and AC are respectively A1, A2 and A3
To prove : A3 = A1 + A2
Proof : In ∆ABC, by Pythagoras theorem,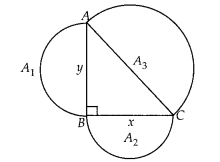

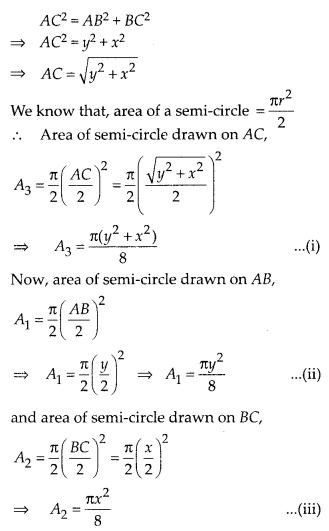
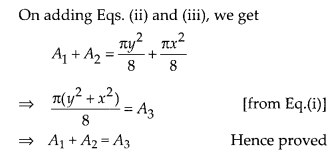
Question 18.
Prove that the area of the equilateral triangle drawn on the hypotenuse of a right angled triangle is equal to the sum of the areas of the equilateral triangles drawn on the other two sides of the triangle.
Solution:
Lett a right triangle BAC in which ∠A is right angle and AC = y, AB = x
Three equilateral triangles ∆AEC, ∆AFB and ∆CBD are drawn on the three sides of ∆ABC.
Again, let area of triangles made on AC, AB and BC are A1, A2 and A3, respectively.
To prove : A3 = A1 + A2
Proof : In ∆CAB, by Pythagoras theorem,
BC2 = AC2 + AB2
⇒ BC2 = y2 + x2
⇒ BC = 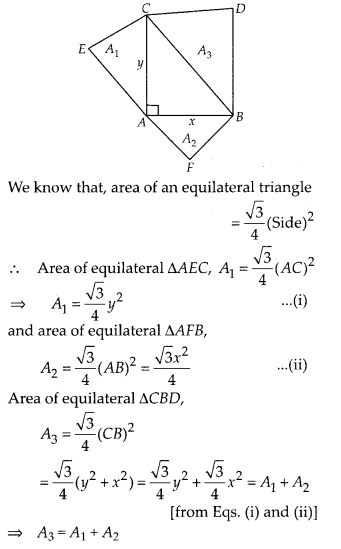y2+x2−−−−−−√

Triangles Class 10 Important Questions Very Short Answer (1 Mark)

Question 1.
If ∆ABC ~ ∆PQR, perimeter of ∆ABC = 32 cm, perimeter of ∆PQR = 48 cm and PR = 6 cm, then find the length of AC. (2012)
Solution:
∆ABC ~ ∆PQR …[Given

Question 2.
∆ABC ~ ∆DEF. If AB = 4 cm, BC = 3.5 cm, CA = 2.5 cm and DF = 7.5 cm, find the perimeter of ∆DEF. (2012, 2017D)
Solution:
∆ABC – ∆DEF …[Given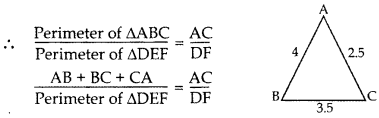

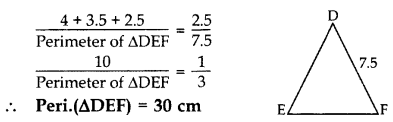
Question 3.
If ∆ABC ~ ∆RPQ, AB = 3 cm, BC = 5 cm, AC = 6 cm, RP = 6 cm and PQ = 10, then find QR. (2014)
Solution:
∆ABC ~ ∆RPQ …[Given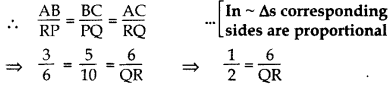

∴ QR = 12 cm

Question 4.
In ∆DEW, AB || EW. If AD = 4 cm, DE = 12 cm and DW = 24 cm, then find the value of DB. (2015)
Solution:
Let BD = x cm
then BW = (24 – x) cm, AE = 12 – 4 = 8 cm
In ∆DEW, AB || EW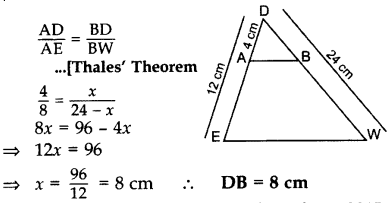

Question 5.
In ∆ABC, DE || BC, find the value of x. (2015)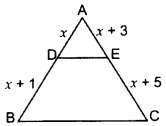

Solution:
In ∆ABC, DE || BC …[Given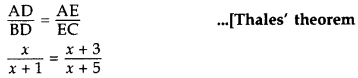

x(x + 5) = (x + 3)(x + 1)
x2 + 5x = x2 + 3x + x + 3
x2 + 5x – x2 – 3x – x = 3
∴ x = 3 cm

Question 6.
In the given figure, if DE || BC, AE = 8 cm, EC = 2 cm and BC = 6 cm, then find DE. (2014)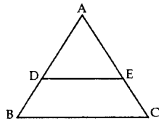

Solution:
In ∆ADE and ∆ABC,
∠DAE = ∠BAC …Common
∠ADE – ∠ABC … [Corresponding angles
∆ADE – ∆ΑΒC …[AA corollary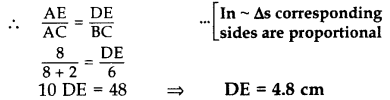

Question 7.
In the given figure, XY || QR, 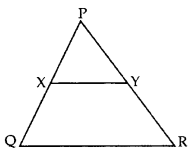PQXQ=73 and PR = 6.3 cm, find YR. (2017OD)

Solution:
Let YR = x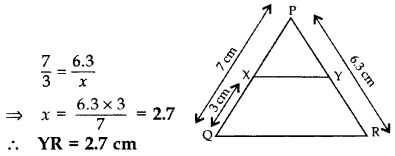
PQXQ=PRYR … [Thales’ theorem

Question 8.
The lengths of the diagonals of a rhombus are 24 cm and 32 cm. Calculate the length of the altitude of the rhombus. (2013)
Solution:
Diagonals of a rhombus are ⊥ bisectors of each other.
∴ AC ⊥ BD,
OA = OC = AC2⇒242 = 12 cm
OB = OD = BD2⇒322 = 16 cm
In rt. ∆BOC,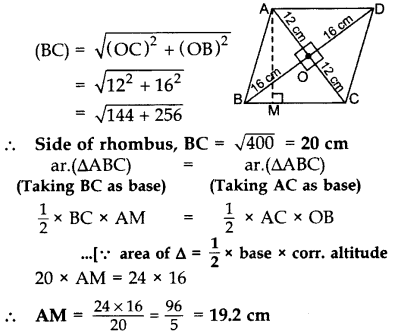

Question 9.
If PQR is an equilateral triangle and PX ⊥ QR, find the value of PX2. (2013)
Solution:
Altitude of an equilateral ∆,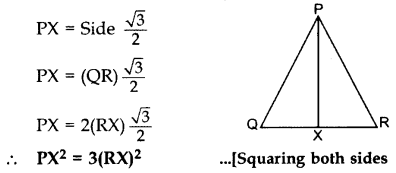

Triangles Class 10 Important Questions Short Answer-I (2 Marks)

Question 10.
The sides AB and AC and the perimeter P, of ∆ABC are respectively three times the corresponding sides DE and DF and the perimeter P, of ∆DEF. Are the two triangles similar? If yes, find ar(△ABC)ar(△DEF) (2012)
Solution:
Given: AB = 3DE and AC = 3DF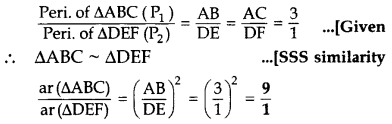

…[∵ The ratio of the areas of two similar ∆s is equal to the ratio of the squares of their corresponding sides

Question 11.
In the figure, EF || AC, BC = 10 cm, AB = 13 cm and EC = 2 cm, find AF. (2014)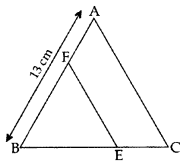

Solution:
BE = BC – EC = 10 – 2 = 8 cm
Let AF = x cm, then BF = (13 – x) cm
In ∆ABC, EF || AC … [Given

Question 12.
X and Y are points on the sides AB and AC respectively of a triangle ABC such that AXAB=14, AY = 2 cm and YC = 6 cm. Find whether XY || BC or not. (2015)
Solution:
Given: 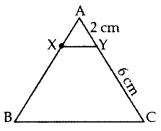AXAB=14

AX = 1K, AB = 4K
∴ BX = AB – AX
= 4K – 1K = 3K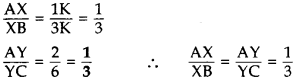

∴ XY || BC … [By converse of Thales’ theorem

Question 13.
In the given figure, ∠A = 90°, AD ⊥ BC. If BD = 2 cm and CD = 8 cm, find AD. (2012; 2017D)

Solution:
∆ADB ~ ∆CDA …[If a perpendicular is drawn from the vertex of the right angle of a rt. ∆ to the hypotenuse then As on both sides of the ⊥ are similar to the whole D and to each other
∴ BDAD=ADCD …[∵ Sides are proportional
AD2 = BD , DC
AD2 = (2) (8) = 16 ⇒ AD = 4 cm

Question 14.
In ∆ABC, ∠BAC = 90° and AD ⊥ BC. Prove that AD\frac{B D}{A D}=\frac{A D}{C D} = BD × DC. (2013)
Solution:
In 1t. ∆BDA, ∠1 + ∠5 = 90°
In rt. ∆BAC, ∠1 + ∠4 = 90° …(ii)
∠1 + ∠5 = ∠1 + ∠4 …[From (i) & (ii)
.. ∠5 = ∠4 …(iii)
In ∆BDA and ∆ADC,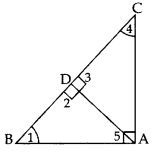

∠5 = 24 … [From (iii)
∠2 = ∠3 …[Each 90°
∴ ∆BDA ~ ∆ADC…[AA similarity
BDAD=ADCD
… [In ~ As corresponding BA sides are proportional
∴ AD2 = BD × DC

Question 15.
A 6.5 m long ladder is placed against a wall such that its foot is at a distance of 2.5 m from the wall. Find the height of the wall where the top of the ladder touches it. (2015)
Solution:
Let AC be the ladder and AB be the wall.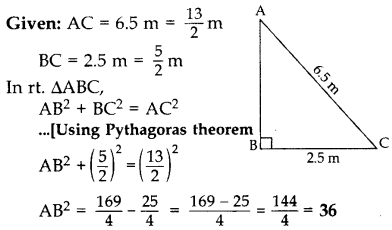

∴Required height, AB = 6 m

Question 16.
In the figure ABC and DBC are two right triangles. Prove that AP × PC = BP × PD. (2013)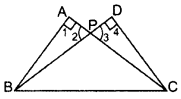

Solution: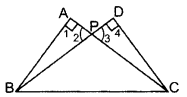

In ∆APB and ∆DPC,
∠1 = ∠4 … [Each = 90°
∠2 = ∠3 …[Vertically opp. ∠s
∴ ∆APB ~ ∆DPC …[AA corollary
⇒ BPPC=APPD … [Sides are proportional
∴ AP × PC = BP × PD

Question 17.
In the given figure, QA ⊥ AB and PB ⊥ AB. If AO = 20 cm, BO = 12 cm, PB = 18 cm, find AQuestion (2017OD)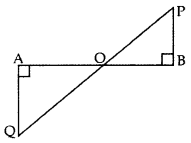

Solution: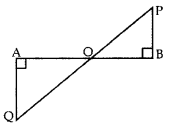

In ∆OAQ and ∆OBP,
∠OAQ = ∠OBP … [Each 90°
∠AOQ = ∠BOP … [vertically opposite angles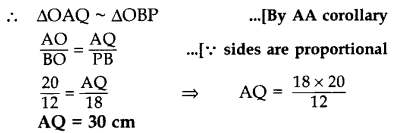

Triangles Class 10 Important Questions Short Answer-II (3 Marks)

Question 18.
In the given figure, CD || LA and DE || AC. Find the length of CL if BE = 4 cm and EC = 2 cm. (2012)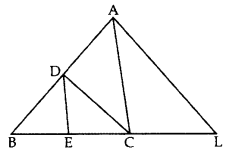

Solution:
In ∆ABL, CD || LA

Question 19.
If a line segment intersects sides AB and AC of a ∆ABC at D and E respectively and is parallel to BC, prove that ADAB=AEAC. (2013)
Solution:
Given. In ∆ABC, DE || BC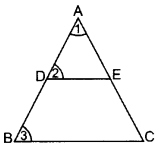

To prove. ADAB=AEAC
Proof.
In ∆ADE and ∆ABC
∠1 = ∠1 … Common
∠2 = ∠3 … [Corresponding angles
∆ADE ~ ∆ABC …[AA similarity
∴ ADAB=AEAC
…[In ~∆s corresponding sides are proportional

Question 20.
In a ∆ABC, DE || BC with D on AB and E on AC. If ADDB=34 , find BCDE. (2013)
Solution:
Given: In a ∆ABC, DE || BC with D on AB and E
on AC and ADDB=34
To find: BCDE
Proof. Let AD = 3k,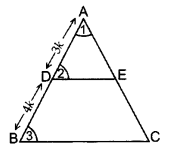

DB = 4k
∴ AB = 3k + 4k = 7k
In ∆ADE and ∆ABC,
∠1 = ∠1 …[Common
∠2 = ∠3 … [Corresponding angles
∴ ∆ADE ~ ∆ABC …[AA similarity

Question 21.
In the figure, if DE || OB and EF || BC, then prove that DF || OC. (2014)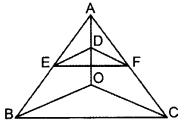

Solution:
Given. In ∆ABC, DE || OB and EF || BC
To prove. DF || OC
Proof. In ∆AOB, DE || OB … [Given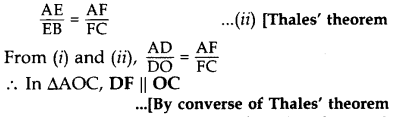

Question 22.
If the perimeters of two similar triangles ABC and DEF are 50 cm and 70 cm respectively and one side of ∆ABC = 20 cm, then find the corresponding side of ∆DEF. (2014)
Solution:

Given. ∆ABC ~ ∆DEF,
Perimeter(∆ABC) = 50 cm
Perimeter(∆DEF) = 70 cm
One side of ∆ABC = 20 cm
To Find. Corresponding side of ∆DEF (i.e.,) DE. ∆ABC ~ ∆DEF …[Given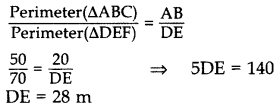

∴ The corresponding side of ADEF = 28 cm

Question 23.
A vertical pole of length 8 m casts a shadow 6 cm long on the ground and at the same time a tower casts a shadow 30 m long. Find the height of tower. (2014)
Solution: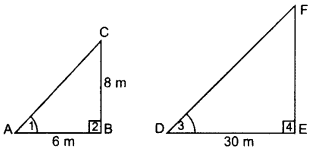

Let BC be the pole and EF be the tower Shadow AB = 6 m and DE = 30 m.
In ∆ABC and ∆DEF,
∠2 = ∠4 … [Each 90°
∠1 = ∠3 … [Sun’s angle of elevation at the same time
∆ABC ~ ∆DEF …[AA similarity
ABDE=BCEF … [In -As corresponding sides are proportional
⇒ 630=8EF ∴ EF = 40 m

Question 24.
In given figure, EB ⊥ AC, BG ⊥ AE and CF ⊥ AE (2015)
Prove that:
(a) ∆ABG ~ ∆DCB
(b) 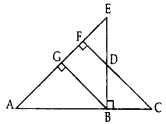BCBD=BEBA

Solution: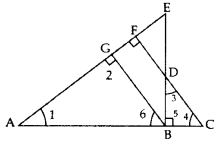

Given: EB ⊥ AC, BG ⊥ AE and CF ⊥ AE.
To prove: (a) ∆ABG – ∆DCB,
(b) BCBD=BEBA
Proof: (a) In ∆ABG and ∆DCB,
∠2 = ∠5 … [each 90°
∠6 = ∠4 … [corresponding angles
∴ ∆ABG ~ ∆DCB … [By AA similarity
(Hence Proved)
∴ ∠1 = ∠3 …(CPCT … [In ~∆s, corresponding angles are equal

(b) In ∆ABE and ∆DBC,
∠1 = ∠3 …(proved above
∠ABE = ∠5 … [each is 90°, EB ⊥ AC (Given)
∆ABE ~ ∆DBC … [By AA similarity
BCBD=BEBA
… [In ~∆s, corresponding sides are proportional
∴ BCBD=BEBA (Hence Proved)

Question 25.
∆ABC ~ ∆PQR. AD is the median to BC and PM is the median to QR. Prove that ABPQ=ADPM. (2017D)
Solution: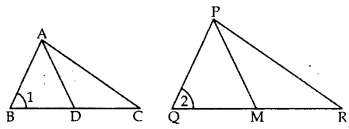

∆ABC ~ ∆PQR … [Given
∠1 = ∠2 … [In ~∆s corresponding angles are equal

Question 26.
State whether the given pairs of triangles are similar or not. In case of similarity mention the criterion. (2015)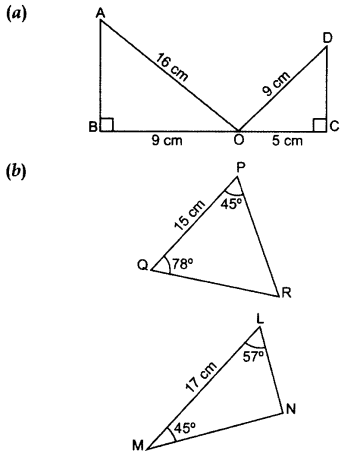

Solution:

(b) In ∆PQR, ∠P + ∠Q + ∠ZR = 180° …[Angle-Sum Property of a ∆
45° + 78° + ∠R = 180°
∠R = 180° – 45° – 78° = 57°
In ∆LMN, ∠L + ∠M + ∠N = 180° …[Angle-Sum Property of a ∆
57° + 45° + ∠N = 180°
∠N = 180° – 57 – 45° = 78°
∠P = ∠M … (each = 45°
∠Q = ∠N … (each = 78°
∠R = ∠L …(each = 57°
∴ ∆PQR – ∆MNL …[By AAA similarity theorem

Question 27.
In the figure of ∆ABC, D divides CA in the ratio 4 : 3. If DE || BC, then find ar (BCDE) : ar (∆ABC). (2015)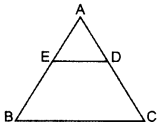

Solution:
Given:
D divides CA in 4 : 3
CD = 4K
DA = 3K
DE || BC …[Given

In ∆AED and ∆ABC,
∠1 = ∠1 …[common
∠2 = ∠3 … corresponding angles
∴ ∆AED – ∆ABC …(AA similarity
⇒ ar(△AED)ar(△ABC)=(ADAC)2
… [The ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides
⇒ frac(3K)2(7K)2=9K249K2=ar(△AED)ar(△ABC)=949
Let ar(∆AED) = 9p
and ar(∆ABC) = 49p
ar(BCDE) = ar (∆ABC) – ar (∆ADE)
= 49p – 9p = 40p
∴ ar(BCDE)ar(△ABC)=40p49p
∴ ar (BCDE) : ar(AABC) = 40 : 49

Question 28.
In the given figure, DE || BC and AD : DB = 7 : 5, find \frac { ar\left( \triangle DEF \right) }{ ar\left( \triangle CFB \right) } [/latex] (2017OD)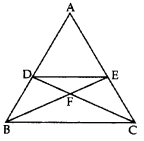

Solution:
Given: In ∆ABC, DE || BC and AD : DB = 7 : 5.
To find: 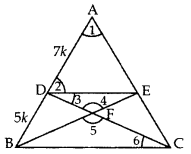ar(△DEF)ar(△CFB) = ?

Proof: Let AD = 7k
and BD = 5k then
AB = 7k + 5k = 12k
In ∆ADE and ∆ABC,
∠1 = ∠1 …(Common
∠2 = ∠ABC … [Corresponding angles

Question 29.
In the given figure, the line segment XY is parallel to the side AC of ∆ABC and it divides the triangle into two parts of equal areas. Find the ratio 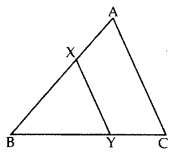AXAB. (2017OD)

Solution:
We have XY || AC … [Given
So, ∠BXY = ∠A and ∠BYX = ∠C …[Corresponding angles
∴ ∆ABC ~ ∆XBY …[AA similarity criterion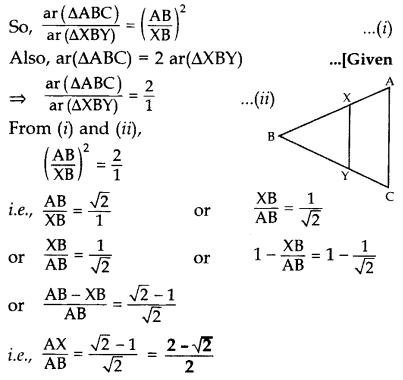

Question 30.
In the given figure, AD ⊥ BC and BD = 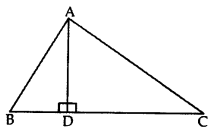13CD. Prove that 2AC2 = 2AB2 + BC2. (2012)

Solution:
BC = BD + DC = BD + 3BD = 4BD
∴ BC4 = BD
In rt. ∆ADB, AD2 = AB2 – BD2 ….(ii)
In rt. ∆ADC, AD2 = AC2 – CD2 …(iii)
From (ii) and (iii), we get
AC2 – CD2 = AB2 – BD2
AC2 = AB2 – BD2 + CD2

∴ 2AC2 = 2AB2 + BC2 (Hence proved)

Question 31.
In the given figure, ∆ABC is right-angled at C and DE ⊥ AB. Prove that ∆ABC ~ ∆ADE and hence find the lengths of AE and DE. (2012, 2017D)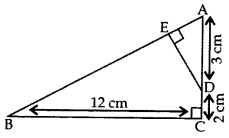

Solution:
Given: ∆ABC is rt. ∠ed at C and DE ⊥ AB.
AD = 3 cm, DC = 2 cm, BC = 12 cm
To prove:
(i) ∆ABC ~ ∆ADE; (ii) AE = ? and DE = ?
Proof. (i) In ∆ABC and ∆ADE,
∠ACB = ∠AED … [Each 90°
∠BAC = ∠DAE …(Common .
∴ ∆ABC ~ ∆ADE …[AA Similarity Criterion

(ii) ∴ ABAD=BCDE=ACAE … [side are proportional
AB3=12DE=3+2AE
…..[In rt. ∆ACB, … AB2 = AC2 + BC2 (By Pythagoras’ theorem)
= (5)2 + (12)2 = 169
∴ AB = 13 cm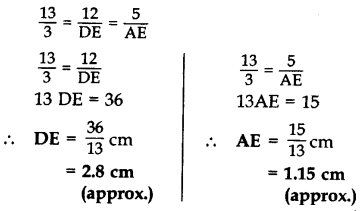

Question 32.
In ∆ABC, if AP ⊥ BC and AC2 = BC2 – AB2, then prove that PA2 = PB × CP. (2015)
Solution: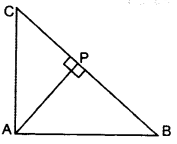

AC2 = BC2 – AB2 …Given
AC2 + AB2 = BC2
∴ ∠BAC = 90° … [By converse of Pythagoras’ theorem
∆APB ~ ∆CPA
[If a perpendicular is drawn from the vertex of the right angle of a triangle to the hypotenuse then As on both sides of the perpendicular are similar to the whole triangle and to each other.
∴ APCP=PBPA … [In ~∆s, corresponding sides are proportional
∴ PA2 = PB. CP (Hence Proved)

Question 33.
ABCD is a rhombus. Prove that AB2 + BC2 + CD2 + DA2 = AC2 + BD2. (2013)
Solution:
Given. In rhombus ABCD, diagonals AC and BD intersect at O.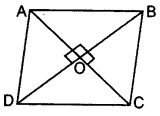

To prove: AB2 + BC2 + CD2 + DA2 = AC2 + BD2
Proof: AC ⊥ BD [∵ Diagonals of a rhombus bisect each other at right angles
∴ OA = OC and
OB = OD
In rt. ∆AOB,
AB2 = OA2 + OB2 … [Pythagoras’ theorem
AB2 = (AC2)2+(BD2)2
AB2 = (AC2)2+(BD2)2
4AB2 = AC2 + BD2
AB2 + AB2 + AB2 + AB2 = AC2 + BD2
∴ AB2 + BC2 + CD2 + DA2 = AC2 + BD2
…[∵ In a rhombus, all sides are equal

Question 34.
The diagonals of trapezium ABCD intersect each other at point o. If AB = 2CD, find the ratio of area of the ∆AOB to area of ∆COD. (2013)
Solution:
In ∆AOB and ∆COD, … [Alternate int. ∠s
∠1 = ∆3
∠2 = ∠4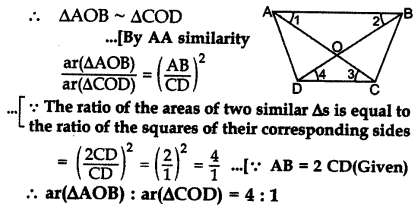

Question 35.
The diagonals of a quadrilateral ABCD intersect each other at the point O such that AOBO=CODO. Show that ABCD is a trapezium. (2014)
Solution:
1st method.
Given: Quadrilateral ABCD in which
AC and BD intersect each other at 0.
Such that AOBO=CODO
To prove: ABCD is a trapezium
Const.: From O, draw OE || CD.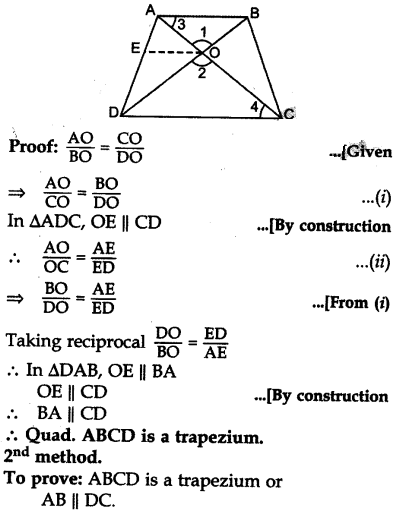


But these are alternate interior angles
∴ AB || DC Quad. ABCD is a trapezium.

Triangles Class 10 Important Questions Long Answer (4 Marks).

Question 36.
In a rectangle ABCD, E is middle point of AD. If AD = 40 m and AB = 48 m, then find EB. (2014D)
Solution: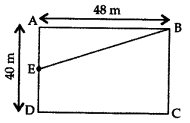

E is the mid-point of AD …[Given
AE = 402 = 20 m
∠A = 90° …[Angle of a rectangle
In rt. ∆BAE,
EB2 = AB2 + AE2 …[Pythagoras’ theorem
= (48)2 + (20)2
= 2304 + 400 = 2704
∴ EB = 2704−−−−√ = 52 m

Question 37.
Let ABC be a triangle and D and E be two points on side AB such that AD = BE. If DP || BC and EQ || AC, then prove that PQ || AB. (2013)
Solution: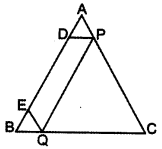

In ∆ABC,
DP || BC
and EQ || AC … [Given

Now, in ∆ABC, P and Q divide sides CA and CB respectively in the same ratio.
∴ PQ || AB

Question 38.
In the figure, ∠BED = ∠BDE & E divides BC in the ratio 2 : 1.
Prove that AF × BE = 2 AD × CF. (2015)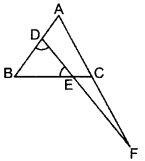

Solution:
Construction:
Draw CG || DF
Proof: E divides
BC in 2 : 1.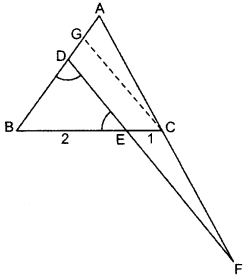
BEEC=21 …(i)

Question 39.
In the given figure, AD = 3 cm, AE = 5 cm, BD = 4 cm, CE = 4 cm, CF = 2 cm, BF = 2.5 cm, then find the pair of parallel lines and hence their lengths. (2015)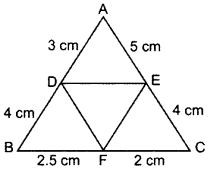

Solution:

Question 40.
If sides AB, BC and median AD of AABC are proportional to the corresponding sides PQ, QR and median PM of PQR, show that ∆ABC ~ ∆PQR. (2017OD)
Solution: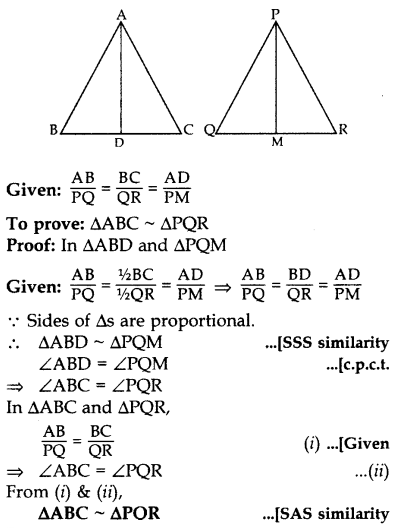

Question 41.
Prove that the ratio of the areas of two similar triangles is equal to the ratio of the squares of their corresponding sides. (2012)
Solution:
Given: ∆ABC ~ ∆DEF

Question 42.
State and prove converse of Pythagoras theorem. Using the above theorem, solve the following: In ∆ABC, AB = 63–√ cm, BC = 6 cm and AC = 12 cm, find ∠B. (2015)
Solution:
Part I:
Statement: Prove that, in a triangle, if square of one side is equal to the sum of the squares of the other two sides, then the angle opposite the first side is a right angle.

To prove: ∠ABC = 90°
Const.: Draw a right angle ∆DEF in which DE = BC and EF = AB.
Proof: In rt. ∆ABC,
AB2 + BC2 = AC2 …(i) Given
In rt. ∆DEF
DE2 + EF2 = DF2 … [By Pythagoras’ theorem
BC2 + AB2 = DF2…(ii)…[∵ DE = BC; EF = AB
From (i) and (ii), we get
AC2 = DF2 = AC = DF
Now, DE = BC …[By construction
EF = AB …[By construction
DF = AC … [Proved above :
∴ ∆DEF = ∆ABC … (SSS congruence :
∴ ∠DEF = ∠ABC …[c.p.c.t.
∵ ∠DEF = 90° ∴ ∠ABC = 90°
Given: In rt. ∆ABC,
AB2 + BC2 = AC2
AB2 + BC2 = (63–√)2 + (6)2
= 108 + 36 = 144 = (12)2
AB2 + BC2 = AC2 ∴ ∠B = 90° … [Above theorem

Question 43.
In the given figure, BL and CM are medians of a triangle ABC, right angled at A. Prove that: 4(BL2 + CM2) = 5BC2 (2012)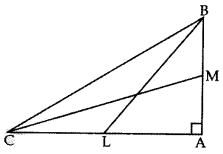

Solution:
Given: BL and CM are medians of ∆ABC, right angled at A.
To prove: 4(BL2 + CM2) = 5 BC2
Proof: In ∆ABC, BC2 = BA2 + CA2 …(i)
In ∆BAL,
BL2 = BA2 + AL2 …[Pythagoras’ theorem
BL2 = BA2 + (CA2)2
BL2 = BA2+ CA24
⇒ 4BL2 = 4BA2 + CA2 …(ii)
Now, In ∆MCA,
MC2 = CA2 + MA2 …[Pythagoras’ theorem
MC2 = CA22 + (BA2)2
MC2 = CA2 + BA24
4MC2 = 4CA2 + BA2
Adding (ii) and (iii), we get
4BL2 + 4MC2 = 4BA2 + CA2 + 4CA2+ BA2 …[From (ii) & (iii)
4(BL2 + MC2) = 5BA2 + 5CA2
4(BL2 + MC2) = 5(BA2 + CA2)
∴ 4(BL2 + MC2) = 5BC2 … [Using (1)
Hence proved.

Question 44.
In the given figure, AD is median of ∆ABC and AE ⊥ BC. (2013)
Prove that b2 + c2 = 2p2 + 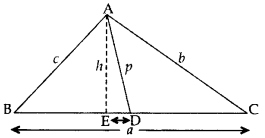12 a2.

Solution: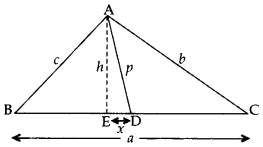

Proof. Let ED = x
BD = DC = BC2=a2 = …[∵ AD is the median
In rt. ∆AEC, AC2 = AE2 + EC2 …..[By Pythagoras’ theorem
b2 = h2 + (ED + DC)2
b2 = (p2 – x2) + (x = a2)2
…[∵ In rt. ∆AED, x2 + h2 = p2 ⇒ h2 = p2 – x2 …(i)
b2 = p2 – x2 + x2 + (a2)22+ 2(x)(a2)
b2 = p2 + ax + a24 …(ii)
In rt. ∆AEB, AB2 = AE2 + BE2 … [By Pythagoras’ theorem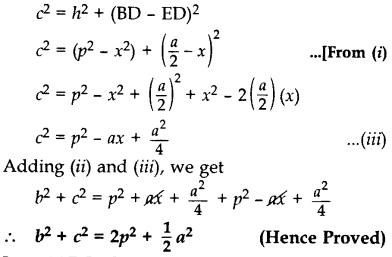

Question 45.
In a ∆ABC, the perpendicular from A on the side BC of a AABC intersects BC at D such that DB = 3 CD. Prove that 2 AB2 = 2 AC2 + BC2. (2013; 2017OD)
Solution:
In rt. ∆ADB,
AD2 = AB2 – BD2 …(i) [Pythagoras’ theorem
In rt. ∆ADC,
AD2 = AC2 – DC2 …(ii) [Pythagoras’ theorem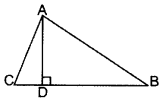

From (i) and (ii), we get
AB2 – BD2 = AC2 – DC2
AB2 = AC2 + BD2 – DC2
Now, BC = BD + DC
= 3CD + CD = 4 CD …[∵ BD = 3CD (Given)
⇒ BC2 = 16 CD2 …(iv) [Squaring
Now, AB2 = AC2 + BD2 – DC2 …[From (iii)
= AC2 + 9 DC2 – DC2 ….[∵ BD = 3 CD ⇒ BD2 = 9 CD2
= AC2 + 8 DC2
= AC2 + 16DC22
= AC2 + BC22 … [From (iv)
∴ 2AB2 = 2AC2 + BC2 … [Proved

Question 46.
In ∆ABC, altitudes AD and CE intersect each other at the point P. Prove that: (2014)
(i) ∆APE ~ ∆CPD
(ii) AP × PD = CP × PE
(iii) ∆ADB ~ ∆CEB
(iv) AB × CE = BC × AD
Solution: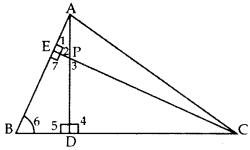

Given. In ∆ABC, AD ⊥ BC & CE ⊥ AB.
To prove. (i) ∆APE ~ ∆CPD
(ii) AP × PD = CP × PE
(iii) ∆ADB ~ ∆CEB
(iv) AB × CE = BC × AD
Proof: (i) In ∆APE and ∆CPD,
∠1 = ∠4 …[Each 90°
∠2 = ∠3 …[Vertically opposite angles
∴ ∆APE ~ ∆CPD …[AA similarity
(ii) APCP=PEPD … [In ~ ∆s corresponding sides are proportional
∴ AP × PD = CP × PE
(iii) In ∆ADB and ∆CEB,
∠5 = ∠7 …[Each 90°
∠6 = ∠6 …(Common
∴ ∆ADB ~ ∆CEB …[AA similarity
(iv) ∴ ABCB=ADCE … [In ~ ∆s corresponding sides are proportional
∴ AB × CE = BC × AD

Question 47.
In the figure, PQR and QST are two right triangles, right angled at R and T resepctively. Prove that QR × QS = QP × QT. (2014)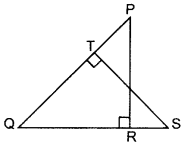

Solution:
Given: Two rt. ∆’s PQR and QST.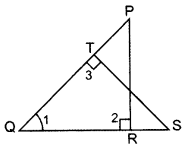

To prove: QR × QS = QP × QT
Proof: In ∆PRQ and ∆STQ,
∠1 = ∠1 … [Common
∠2 = ∠3 … [Each 90°
∆PRQ ~ ∆STO …(AA similarity
∴ QRQT=QPQS ..[In -∆s corresponding sides are proportional
∴ QR × QS = QP × QT (Hence proved)

Question 48.
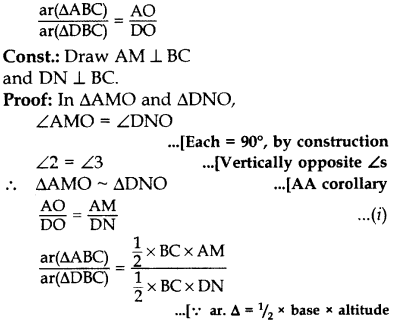
In the given figure, ABC and DBC are two triangles on the same base BC. If AD intersects BC at O, show that ar(ABC)ar(DBC)=AODO. (2012)

Solution:
Given: ABC and DBC are two As on the same base BC. AD intersects BC at O.
To prove: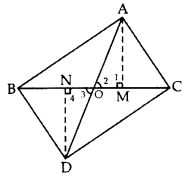

Question 49.
Hypotenuse of a right triangle is 25 cm and out of the remaining two sides, one is longer than the other by 5 cm. Find the lengths of the other
two sides. (2013)
Solution:
Let Base, AB = x cm
Then altitude, BC = (x + 5) cm
In rt. ∆,
By Pythagoras’ theorem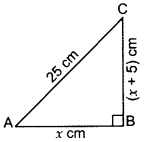

AB2 + BC2 = AC2
⇒ (x)2 + (x + 5)2 = 252
⇒ x22 + x2 + 10x + 25 – 625 = 0
⇒ 2x2 + 10x – 600 = 0
⇒ x2 + 5x – 300 = 0 … [Dividing both sides by 2
⇒ x2 + 20x – 15x – 300 = 0
⇒ x(x + 20) – 15(x + 20) = 0
(x – 15)(x + 20) = 0
x – 15 = 0 or x + 20 = 0
x = 15 or x = -20
Base cannot be -ve
∴ x = 15 cm
∴ Length of the other side = 15 + 5 = 20 cm
Two sides are = 15 cm and 20 cm

Question 50.
In Figure, AB ⊥ BC, FG ⊥ BC and DE ⊥ AC. Prove that ∆ADE ~ ∆GCF. (2016 OD)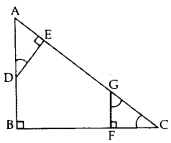

Solution:
In rt. ∆ABC,
∠A + ∠C = 90° …(i)
In rt. ∆AED,
∠A + ∠2 = 90°
From (i) and (ii), ∠C = ∠2
Similarly, ∠A = ∠1
Now in ∆ADE & ∆GCF
∠A = 1 … [Proved
∠C = 2 … [Proved
∠AED = ∠GFC … [rt. ∠s
∴ ∆ADE – ∆GCF …(Hence Proved)

Class 10 Maths Notes Chapter 6 Triangles

SIMILAR FIGURES

• Two figures having the same shape but not necessary the same size are called similar figures.
• All congruent figures are similar but all similar figures are not congruent.

SIMILAR POLYGONS
Two polygons are said to be similar to each other, if:
(i) their corresponding angles are equal, and
(ii) the lengths of their corresponding sides are proportional

Example:
Any two line segments are similar since length are proportional

Any two circles are similar since radii are proportional

Any two squares are similar since corresponding angles are equal and lengths are proportional.

Note:
Similar figures are congruent if there is one to one correspondence between the figures.
∴ From above we deduce:

Any two triangles are similar, if their

(i) Corresponding angles are equal
∠A = ∠P
∠B = ∠Q
∠C = ∠R

(ii) Corresponding sides are proportional
ABPQ=ACPR=BCQR

THALES THEOREM OR BASIC PROPORTIONALITY THEORY

Theorem 1:
State and prove Thales’ Theorem.
Statement:
If a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, the other two sides are divided in the same ratio.

Given: In ∆ABC, DE || BC.
To prove: ADDB=AEEC
Const.: Draw EM ⊥ AD and DN ⊥ AE. Join B to E and C to D.
Proof: In ∆ADE and ∆BDE,
ar(ΔADE)ar(ΔBDE)=12×AD×EM12×DB×EM=ADDB ……..(i) [Area of ∆ = 12 x base x corresponding altitude
In ∆ADE and ∆CDE,
ar(ΔADE)ar(ΔCDE)=12×AE×DN12×EC×DN=AEEC
∵ DE || BC …[Given
∴ ar(∆BDE) = ar(∆CDE)
…[∵ As on the same base and between the same parallel sides are equal in area
From (i), (ii) and (iii),
ADDB=AEEC

CRITERION FOR SIMILARITY OF TRIANGLES

Two triangles are similar if either of the following three criterion’s are satisfied:

• AAA similarity Criterion. If two triangles are equiangular, then they are similar.
• Corollary(AA similarity). If two angles of one triangle are respectively equal to two angles of another triangle, then the two triangles are similar.
• SSS Similarity Criterion. If the corresponding sides of two triangles are proportional, then they are similar.
• SAS Similarity Criterion. If in two triangles, one pair of corresponding sides are proportional and the included angles are equal, then the two triangles are similar.

Results in Similar Triangles based on Similarity Criterion:

1. Ratio of corresponding sides = Ratio of corresponding perimeters
2. Ratio of corresponding sides = Ratio of corresponding medians
3. Ratio of corresponding sides = Ratio of corresponding altitudes
4. Ratio of corresponding sides = Ratio of corresponding angle bisector segments.

AREA OF SIMILAR TRIANGLES

Theorem 2.
The ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides.
Given: ∆ABC ~ ∆DEF
To prove: ar(ΔABC)ar(ΔDEF)=AB2DE2=BC2EF2=AC2DF2
Const.: Draw AM ⊥ BC and DN ⊥ EF.
Proof: In ∆ABC and ∆DEF

ar(ΔABC)ar(ΔDEF)=12×BC×AM12×EF×DN=BCEF.AMDN …(i) ……[Area of ∆ = 12 x base x corresponding altitude
∵ ∆ABC ~ ∆DEF
∴ ABDE=BCEF …..(ii) …[Sides are proportional
∠B = ∠E ……..[∵ ∆ABC ~ ∆DEF
∠M = ∠N …..[each 90°
∴ ∆ABM ~ ∆DEN …………[AA similarity
∴ ABDE=AMDN …..(iii) …[Sides are proportional
From (ii) and (iii), we have: BCEF=AMDN …(iv)
From (i) and (iv), we have: ar(ΔABC)ar(ΔDEF)=BCEF.BCEF=BC2EF2
Similarly, we can prove that
ar(ΔABC)ar(ΔDEF)=AB2DE2=AC2DF2
∴ar(ΔABC)ar(ΔDEF)=AB2DE2=BC2EF2=AC2DF2

Results based on Area Theorem:

1. Ratio of areas of two similar triangles = Ratio of squares of corresponding altitudes
2. Ratio of areas of two similar triangles = Ratio of squares of corresponding medians
3. Ratio of areas of two similar triangles = Ratio of squares of corresponding angle bisector segments.

Note:
If the areas of two similar triangles are equal, the triangles are congruent.

PYTHAGORAS THEOREM

Theorem 3:
State and prove Pythagoras’ Theorem.
Statement:
Prove that, in a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
Given: ∆ABC is a right triangle right-angled at B.
To prove: AB² + BC² = AC²
Const.: Draw BD ⊥ AC
Proof: In ∆s ABC and ADB,

∠A = ∠A …[common
∠ABC = ∠ADB …[each 90°
∴ ∆ABC ~ ∆ADB …[AA Similarity
∴ ABAD=ACAB ………[sides are proportional]
⇒ AB² = AC.AD
Now in ∆ABC and ∆BDC
∠C = ∠C …..[common]
∠ABC = ∠BDC ….[each 90°]
∴ ∆ABC ~ ∆BDC …..[AA similarity]
∴ BCDC=ACBC ……..[sides are proportional]
BC² = AC.DC …(ii)
On adding (i) and (ii), we get
AB² + BC² = ACAD + AC.DC
⇒ AB² + BC² = AC.(AD + DC)
AB² + BC² = AC.AC
∴AB² + BC² = AC²

CONVERSE OF PYTHAGORAS THEOREM

Theorem 4:
State and prove the converse of Pythagoras’ Theorem.
Statement:
Prove that, in a triangle, if square of one side is equal to the sum of the squares of the other two sides, then the angle opposite the first side is a right angle.

Given: In ∆ABC, AB² + BC² = AC²
To prove: ∠ABC = 90°
Const.: Draw a right angled ∆DEF in which DE = AB and EF = BC
Proof: In ∆ABC,
AB² + BC² = AC² …(i) [given]
In rt. ∆DEF
DE² + EF² = DF² …[by pythagoras theorem]
AB² + BC² = DF² …..(ii) …[DE = AB, EF = BC]
From (i) and (ii), we get
AC² = DF²
⇒ AC = DF
Now, DE = AB …[by cont]
EF = BC …[by cont]
DF = AC …….[proved above]
∴ ∆DEF ≅ ∆ABC ……[sss congruence]
∴ ∠DEF = ∠ABC …..[CPCT]
∠DEF = 90° …[by cont]
∴ ∠ABC = 90°

Results based on Pythagoras’ Theorem:
(i) Result on obtuse Triangles.
If ∆ABC is an obtuse angled triangle, obtuse angled at B,
If AD ⊥ CB, then
AC² = AB² + BC² + 2 BC.BD

(ii) Result on Acute Triangles.
If ∆ABC is an acute angled triangle, acute angled at B, and AD ⊥ BC, then
AC² = AB² + BC² – 2 BD.BC.

Here Is The Class 10 Maths All NCERT Solutions In Hindi + English With Extra Questions, Notes And Important Questions

• Chapter 1 Real Numbers
• Chapter 2 Polynomials
• Chapter 3 Pair of Linear Equations in Two Variables
• Chapter 4 Quadratic Equations
• Chapter 5 Arithmetic Progressions
• Chapter 6 Triangles
• Chapter 7 Coordinate Geometry
• Chapter 8 Introduction to Trigonometry
• Chapter 9 Applications of Trigonometry
• Chapter 10 Circle
• Chapter 11 Constructions
• Chapter 12 Areas related to Circles
• Chapter 13 Surface Areas and Volumes
• Chapter 14 Statistics
• Chapter 15 Probability